Giải SBT Toán 10 trang 80 Tập 1 Cánh diều

Với Giải sách bài tập Toán 10 trang 80 Tập 1 trong Bài 2: Giải tam giác. Tính diện tích tam giác SBT Toán 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 80.

Giải SBT Toán 10 trang 80 Tập 1 Cánh diều

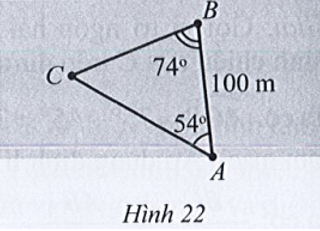
Bài 17 trang 80 SBT Toán 10 Tập 1: Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB = 100m. Hai người tiến hành đo đạc và thu được kết quả (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?

 

Lời giải:

Xét tam giác ABC, có: $\hat{A}+\hat{B}+\hat{C}=180°$ (định lí tổng ba góc)

⇒ $\hat{C}=180°-(\hat{A}+\hat{B})=180°-(54°+74°)=52°$ .

Áp dụng định lí sin, ta được:

⇔ $\frac{BC}{\sin A}=\frac{AB}{\sin C}$

⇔ $\frac{BC}{\sin 54°}=\frac{100}{\sin 52°}$ .

Vậy con tàu cách đảo 102, 7 m.

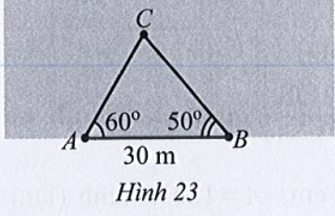
Bài 18 trang 80 SBT Toán 10 Tập 1: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: AB = 30 m, $\widehat{CAB}=60°,\widehat{CBA}=50°$ (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

 

Lời giải:

Xét tam giác ABC, có:

$\hat{A}+\hat{B}+\hat{C}={180}^0$ (định lí tổng ba góc)

⇒ $\hat{C}=180°-(\hat{A}+\hat{B})=180°-(60°+50°)=70°$ .

Áp dụng định lí sin, ta được:

$\frac{AB}{\sin C}=\frac{AC}{\sin B}\iff \frac{30}{\sin 70°}=\frac{AC}{\sin 50°}\iff AC=\frac{30.\sin 50°}{\sin 70°}\approx 24,5$

Vậy khoảng cách từ vị trí A đến con tàu C là 24,5 m.

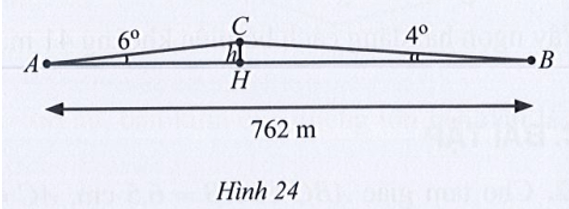
Bài 19 trang 80 SBT Toán 10 Tập 1: Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m,

 

a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng vận tốc trung bình lên dốc là 4km/h và tốc độ khi xuống dốc là 19 km/h.

Lời giải:

a) Đặt AH = x (m) (x > 0)

⇒ BH = AB – AH = 762 – x (m)

Xét tam giác AHC vuông tại H, có:

$\tan A=\frac{CH}{AH}$

⇔ $\tan 6°=\frac{CH}{x}$

⇔ CH = tan6°.x

Xét tam giác BHC vuông tại H, có:

⇔ tan B = $\frac{CH}{BH}$

$\iff \tan 4°=\frac{CH}{762-x}$

⇔ CH = tan4°.(762 – x)

⇒ tan6°.x = tan4°.(762 – x)

⇔ (tan6° + tan4°).x ≈ 53,3

⇔ x ≈ 304,4

⇒ CH ≈ tan6°.304,4 ≈ 32

Vậy chiều cao của con dốc là 32 m.

b) Xét tam giác AHC vuông tại H, có:

sin A = $\frac{CH}{AH}$

⇔ sin $6°=\frac{32}{AC}$

⇔ AC = $\frac{32}{\sin 6°}\approx 306,1m=0,3061km$

Xét tam giác BHC vuông tại H, có:

sin B = $\frac{CH}{CB}$

⇔ $\sin 4°=\frac{32}{AB}$

⇔ $AB=\frac{32}{\sin 4°}\approx 458.7m=0,4587km$

Thời gian bạn AN đi từ nhà đến trường là: $\frac{0,3061}{4}+\frac{0,4587}{19}\approx 0,1\left(giờ\right)=6phút$

Vậy bạn An đến trường lúc: 6 giờ 6 phút.

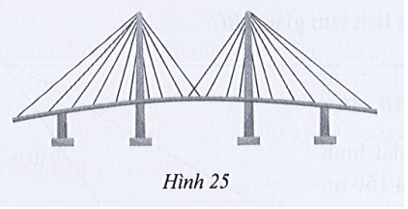
Bài 20 trang 80 SBT Toán 10 Tập 1: Quan sát cây cầu văng minh họa ở Hình 25.

 

 

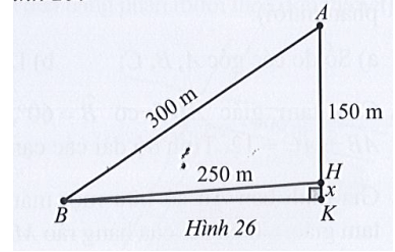
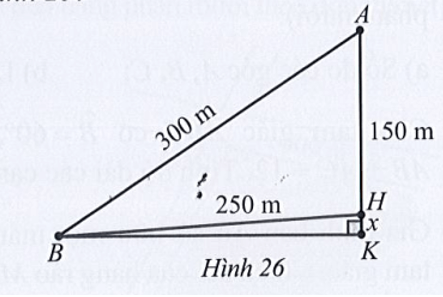
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Lời giải:

 

Xét tam giác ABC, có:

$\cos \widehat{AHB}=\frac{A{H}^2+B{H}^2-A{B}^2}{2.AH.BH}=\frac{{150}^2+{250}^2-{300}^2}{2.150.250}=-\frac{1}{15}$

⇒ $\widehat{AHB}\approx 93,8°$

Ta lại có: $\widehat{AHB}+\widehat{BHK}=180°$

$\widehat{BHK}=180°-\widehat{AHB}=180°-93,8°=86,2°$

Xét tam giác BHK vuông tại K, có:

$\widehat{\mathrm{HBK}}+\widehat{\mathrm{BHK}}={90}^0$ (hai góc phụ nhau)

⇔ $\widehat{HBK}=90°-\widehat{BHK}$

$\iff \widehat{HBK}\approx 90°-86,2°=3,8°$ .

Vậy độ dốc của cầu qua trụ khoảng 3,8°.

Lời giải Sách bài tập Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác Cánh diều hay khác:

• Giải SBT Toán 10 trang 79 Tập 1

• Giải SBT Toán 10 trang 81 Tập 1

Xem thêm lời giải Sách bài tập Toán 10 Cánh diều hay, chi tiết khác:

• SBT Toán 10 Bài 3: Khái niệm vectơ

• SBT Toán 10 Bài 4: Tổng và hiệu của hai vectơ

• SBT Toán 10 Bài 5: Tích của một số với một vectơ

• SBT Toán 10 Bài 6: Tích vô hướng của hai vectơ

• SBT Toán 10 Bài tập cuối chương 4 trang 106, 107, 108

Xem thêm các tài liệu học tốt lớp 10 hay khác:

• Giải sgk Toán 10 Cánh diều
• Giải Chuyên đề học tập Toán 10 Cánh diều
• Giải SBT Toán 10 Cánh diều
• Giải lớp 10 Cánh diều (các môn học)
• Giải lớp 10 Kết nối tri thức (các môn học)
• Giải lớp 10 Chân trời sáng tạo (các môn học)

---