Giải SBT Toán 10 trang 66 Tập 2 Kết nối tri thức
Với Giải SBT Toán 10 trang 66 Tập 2 trong Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 66.
Giải SBT Toán 10 trang 66 Tập 2 Kết nối tri thức
Bài 9.7 trang 66 Sách bài tập Toán lớp 10 Tập 2: Tại một quán ăn, lúc đầu có 50 khách trong đó có 2x đàn ông và y phụ nữ. Sau một tiếng, y – 6 đàn ông ra về và 2x – 5 khách mới đến là nữ. Chọn ngẫu nhiên một khách. Biết rằng xác suất để chọn được một khách nữ là . Tìm x và y.
Hướng dẫn giải:
Theo đề bài ta có:
2x + y = 50 ⇔ y = 50 – 2x.
Sau một tiếng, trong quán có:
50 – (y – 6) + 2x – 5
= 50 – y + 6 + 2x – 5
= 51 + 2x – y (người)
Trong đó, có (2x – 5 + y) người là nữ. Vậy ta có xác suất để chọn được một khách nữ là:
⇔ 459 + 18x – 9y = 26x – 65 + 13y
⇔ 4x + 11y = 262
Mà y = 50 – 2x nên ta có:
4x + 11 . (50 – 2x) = 262
⇔ 18x = 288
⇔ x = 16
Do đó, y = 50 – 2 . 16 = 18.
Vậy x = 16, y = 18.
Bài 9.8 trang 66 Sách bài tập Toán lớp 10 Tập 2: Một lớp có 40 học sinh trong đó có 16 nam. Trong các em nam có 3 em thuận tay trái. Trong các em nữ có 2 em thuận tay trái. Chọn ngẫu nhiên hai em. Tính xác suất để hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái.
Hướng dẫn giải:
Số cách để chọn ngẫu nhiên hai em trong 40 em học sinh là: = 780 (cách).
Do đó, ta có n(Ω) = 780.
Gọi A là biến cố: “Hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái”
Lớp có 40 – 16 = 24 em nữ, trong đó, 24 – 2 = 22 em không thuận tay trái. Do đó, số cách chọn 1 em nữ không thuận tay trái là 22 cách.
Trong lớp có 3 em nam thuận tay trái, do đó, số cách chọn 1 em nam thuận tay trái là 3 cách.
Theo quy tắc nhân ta có: n(A) = 22 . 3 = 66.
Vậy xác suất của biến cố A là: P(A) = .
Bài 9.9 trang 66 Sách bài tập Toán lớp 10 Tập 2: Có ba chiếc hộp trong đó hộp I có một viên bi đỏ, một viên bi xanh, một viên bi vàng; hộp II có một viên bi xanh, một viên bi vàng, hộp III có một viên bi đỏ và một viên bi xanh. Tất cả các viên bi đều có cùng kích thước. Từ mỗi hộp rút ngẫu nhiên một viên bi.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất để trong ba viên bi rút ra có ít nhất một viên bi đỏ bằng cách tính gián tiếp thông qua tính xác suất của biến cố đối.
Hướng dẫn giải:
a)
Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, xanh, vàng.
Ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu:
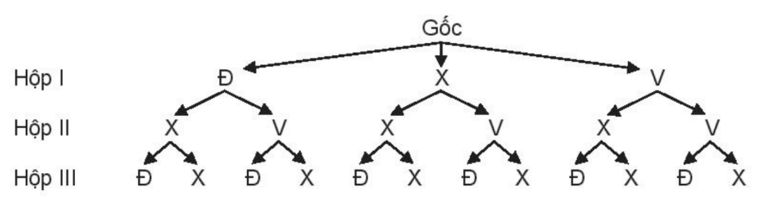
Do đó, ta có:
Ω = {(ĐXĐ; ĐXX; ĐVĐ; ĐVX; XXĐ; XXX; XVĐ; XVX; VXĐ; VXX; VVĐ; VVX}.
Vậy n(Ω) = 12.
b)
Gọi biến cố A: “Trong ba viên bi rút ra có ít nhất một viên bi đỏ”
Biến cố đối của A là 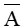
Ta có: 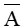
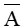
Do đó, ta có:
Vậy
Bài 9.10 trang 66 Sách bài tập Toán lớp 10 Tập 2: Có ba hộp đựng thẻ. Hộp I chứa các tấm thẻ đánh số {1; 2; 3}. Hộp II chứa các tấm thẻ đánh số {2; 4; 6; 8}. Hộp III chứa các tấm thẻ đánh số {1; 3; 5; 7; 9; 11}. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ.
Hướng dẫn giải:
Gọi a là số trên thẻ rút được từ hộp I, a ∈{1; 2; 3}.
Gọi b là số trên thẻ rút được từ hộp II, b ∈{2; 4; 6; 8}.
Gọi c là số trên thẻ rút được từ hộp III, c ∈{1; 3; 5; 7; 9; 11}.
Ta có không gian mẫu: Ω = {(a, b, c) | a ∈{1; 2; 3}, b ∈{2; 4; 6; 8}, c ∈{1; 3; 5; 7; 9; 11}}.
Theo quy tắc nhân, ta có: n(Ω) = 3 . 4 . 6 = 72.
Xét biến cố A: “Tổng ba số trên ba tấm thẻ là số lẻ”.
Do b luôn là một số chẵn và c luôn là một số lẻ nên tổng b + c luôn là một số lẻ, do đó để (a + b + c) là một số lẻ thì a phải là số chẵn. Do đó, a = 2.
Khi đó, A = {(2, b, c) | b ∈{2; 4; 6; 8}, c ∈{1; 3; 5; 7; 9; 11}}.
Do đó, n(A) = 1 . 4 . 6 = 24.
Vậy P(A) = .
Bài 9.11 trang 66 Sách bài tập Toán lớp 10 Tập 2: Trên một dãy phố có 3 quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán để ăn trưa.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau:
E: “Hai người cùng vào một quán”.
F: “Cả hai không chọn quán C”.
Hướng dẫn giải:
a) Sơ đồ hình cây mô tả các phần tử của không gian mẫu là:

b)
Ta có không gian mẫu là:
Ω = {AA; AB; AC; BA; BB; BC; CA; CB; CC}.
Suy ra, n(Ω) = 9.
Ta có biến cố E: “Hai người cùng vào một quán”.
Do đó, E = {AA; BB; CC}; n(E) = 3.
Vậy P(E) = .
Ta có biến cố F: “Cả hai không chọn quán C”.
Do đó, F = {AA; AB; BA; BB}; n(F) = 4.
Vậy P(F) = .
Bài 9.12 trang 66 Sách bài tập Toán lớp 10 Tập 2: Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất để:
• Tất cả đều vào một quán;
• Mỗi quán có đúng 2 bạn vào;
• Quán A có 3 bạn vào, quán B có 1 bạn vào;
• Một quán có 3 bạn vào, quán kia có 1 bạn vào.
Hướng dẫn giải:
a) Sơ đồ hình cây mô tả các phần tử của không gian mẫu là:
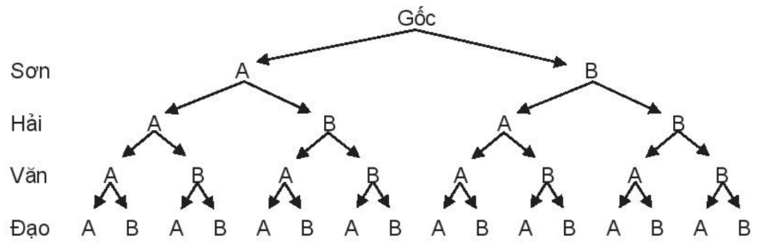
b)
Ta có không gian mẫu:
Ω = {AAAA; AAAB; AABA; AABB; ABAA; ABAB; ABBA; ABBB; BAAA; BAAB; BABA; BABB; BBAA; BBAB; BBBA; BBBB}.
Do đó, n(Ω) = 16.
Gọi biến cố E: “Tất cả đều vào một quán”. Ta có:
E = {AAAA; BBBB}, n(E) = 2, suy ra P(E) = .
Gọi biến cố F: “Mỗi quán có đúng hai bạn vào”. Ta có:
F = {AABB; ABAB; ABBA; BAAB; BABA; BBAA}, n(F) = 6,
suy ra P(F) = .
Gọi biến cố G: “Quán A có 3 bạn vào, quán B có 1 bạn vào”. Ta có:
G = {AAAB; AABA; ABAA; BAAA}, n(G) = 4, suy ra P(G) =
Gọi biến cố K: “Một quán có 3 bạn vào, quán kia có 1 bạn vào.”. Ta có:
K1: “Quán A có 3 bạn vào, quán B có 1 bạn vào” nên K1 = G, n(K1) = 4.
K2: “Quán B có 3 bạn vào, quán A có 1 bạn vào”. Ta có:
K2 = {BBBA; BBAB; BABB; ABBB}, n(K2) = 4
n(K) = n(K1) + n(K2) = 4 + 4 = 8.
Vậy P(K) = .
Xem thêm lời Giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Kết nối tri thức
- Giải Chuyên đề học tập Toán 10 Kết nối tri thức
- Giải SBT Toán 10 Kết nối tri thức
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 10 (hay nhất) - KNTT
- Soạn văn 10 (ngắn nhất) - KNTT
- Soạn văn 10 (siêu ngắn) - KNTT
- Giải sgk Toán 10 - KNTT
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - KNTT
- Giải sgk Hóa học 10 - KNTT
- Giải sgk Sinh học 10 - KNTT
- Giải sgk Địa lí 10 - KNTT
- Giải sgk Lịch sử 10 - KNTT
- Giải sgk Kinh tế và Pháp luật 10 - KNTT
- Giải sgk Tin học 10 - KNTT
- Giải sgk Công nghệ 10 - KNTT
- Giải sgk Hoạt động trải nghiệm 10 - KNTT
- Giải sgk Giáo dục quốc phòng 10 - KNTT

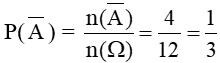
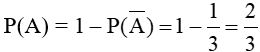



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

