Giải SBT Toán 7 trang 52 Tập 2 Kết nối tri thức

Với Giải SBT Toán 7 trang 52 Tập 2 trong Bài 33: Quan hệ giữa ba cạnh của một tam giác Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 52.

Giải SBT Toán 7 trang 52 Tập 2 Kết nối tri thức

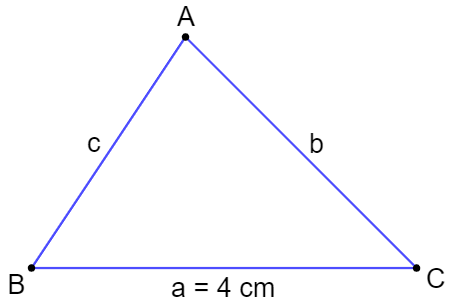
Bài 9.10 trang 52 sách bài tập Toán lớp 7 Tập 2: Cho tam giác có độ dài cạnh lớn nhất bằng 4 cm. Hãy giải thích tại sao chu vi tam giác đó bé hơn 12 cm và lớn hơn 8 cm.

Lời giải:

Gọi độ dài ba cạnh tam giác là a, b, c (cm), (a > b > c).

Cạnh lớn nhất là a = 4, b < 4, c < 4.

Chu vi tam giác là: a + b + c < 4 + 4 + 4 = 12.

Mặt khác, theo bất đẳng thức tam giác: b + c > a

Hay a + b + c > a + a

Suy ra a + b + c > 2a = 8

Do đó 8 < a + b + c < 12

Vậy chu vi tam giác đó bé hơn 12 cm và lớn hơn 8 cm.

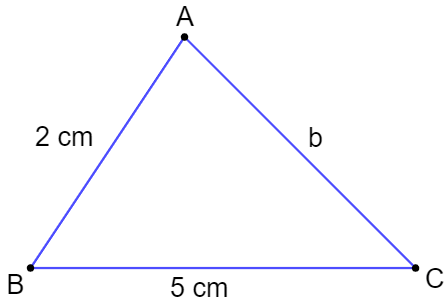
Bài 9.11 trang 52 sách bài tập Toán lớp 7 Tập 2: Tam giác ABC có AB = 2 cm, BC = 5 cm, AC = b (cm) với b là một số nguyên. Hỏi b có thể bằng bao nhiêu?

Lời giải:

Theo bất đẳng thức tam giác, ta có:

BC − AB < AC < BC + AB

Hay 5 − 2 < b < 5 + 2

Do đó 3 < b < 7

Mà b là số nguyên nên b ∈ {4; 5; 6}.

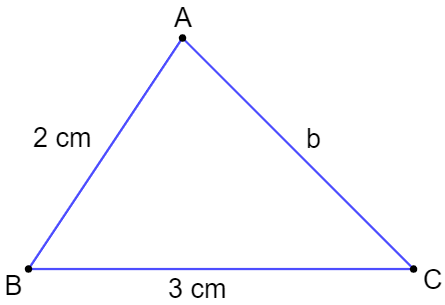
Bài 9.12 trang 52 sách bài tập Toán lớp 7 Tập 2: Tam giác ABC có AB = 2 cm, BC = 3 cm. Đặt CA = b (cm).

a) Chứng minh rằng 1 < b < 5.

b) Giả sử rằng với 1 < b < 5, có tam giác ABC thỏa mãn AB = 2 cm, BC = 3 cm, CA = b (cm). Với mỗi tam giác đó, hãy sắp xếp ba góc A, B, C theo thứ tự từ bé đến lớn.

Lời giải:

a) Theo bất đẳng thức tam giác, ta có:

BC − AB < AC < BC + AB

Hay 3 − 2 < b < 3 + 2

Do đó 1 < b < 5 (đpcm).

b)

+) Với 1 < b ≤ 2, ta có: AC ≤ AB < BC.

Xét tam giác ABC có AC ≤ AB < BC nên suy ra $\hat{B}\le \hat{C}<\hat{A}$ .

+) Với 2 < b ≤ 3, ta có: AB ≤ AC < BC.

Xét tam giác ABC có AB ≤ AC < BC nên suy ra $\hat{C}\le \hat{B}<\hat{A}$.

+) Với 3 < b < 5, ta có: AB ≤ BC < AC.

Xét tam giác ABC có AB ≤ BC < AC nên suy ra $\hat{C}\le \hat{A}<\hat{B}$.

Bài 9.13 trang 52 sách bài tập Toán lớp 7 Tập 2:

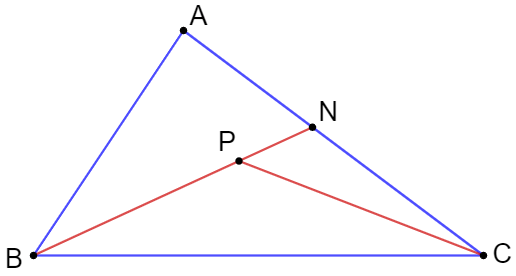
a) Cho P là một điểm bên trong tam giác ABC. Chứng minh rằng:

AB + AC > PB + PC.

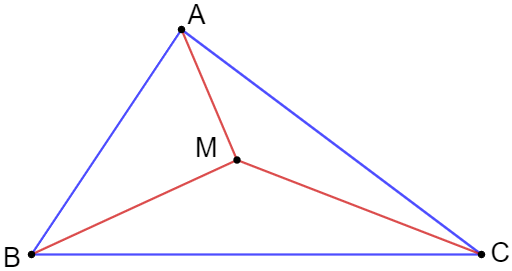
b) Cho M là một điểm bên trong tam giác ABC. Chứng minh rằng:

$\frac{1}{2}\left(AB+BC+CA\right)<MA+MB+MC<AB+BC+CA$.

Lời giải:

a)

Lấy N là giao điểm của đường thẳng AC và BP.

Ta có: AB + AC = AB + (AN + NC) = (AB + AN) + NC (1)

Áp dụng bất đẳng thức tam giác vào tam giác ABN nên suy ra: AB + AN > BN (2)

Từ (1) và (2) suy ra: AB + AC > BN + NC = (BP + NP) + NC = PB + (NP + NC) (3)

Áp dụng bất đẳng thức tam giác vào tam giác CPN nên suy ra:

NP + NC > PC (4)

Từ (3) và (4) suy ra: AB + AC > PB + PC (đpcm).

b)

Áp dụng bất đẳng thức tam giác vào tam giác MAB ta có:

MA + MB > AB (5)

Tương tự với các tam giác MBC và MAC ta lần lượt suy ra được:

MB + MC > BC và MA + MC > AC (6).

Từ (5) và (6) ta suy ra được:

(MA + MB) + (MB + MC) + (MA + MC) > AB + BC + AC

Hay 2(MA + MB + MC) > AB + BC + AC

Suy ra $\frac{1}{2}\left(AB+BC+CA\right)<MA+MB+MC(\ast )$

Mặt khác chứng minh tương tự theo a) ta có:

AB + AC > MB + MC; AC + BC > MA + MB; BC + BA > MC + MA.

Từ đó ta suy ra được:

(MA + MB) + (MB + MC) + (MA + MC) < (AC + AB) + (AB + AC) + (BC + BA)

Hay 2(MA + MB + MC) < 2(AB + BC + CA)

Suy ra MA + MB + MC < AB + BC + CA (**)

Từ (*) và (**) ta suy ra:

$\frac{1}{2}\left(AB+BC+CA\right)<MA+MB+MC<AB+BC+CA$(đpcm).

Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

• SBT Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

• SBT Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

• SBT Toán 7 Ôn tập chương 9

• SBT Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

• SBT Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

Xem thêm các tài liệu học tốt lớp 7 hay khác:

• Giải sgk Toán 7 Kết nối tri thức
• Giải SBT Toán 7 Kết nối tri thức
• Giải lớp 7 Kết nối tri thức (các môn học)
• Giải lớp 7 Chân trời sáng tạo (các môn học)
• Giải lớp 7 Cánh diều (các môn học)

---