Giải Toán 12 trang 43 Tập 2 Cánh diều
Với Giải Toán 12 trang 43 Tập 2 trong Bài tập cuối chương 4 Toán 12 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 43.
Giải Toán 12 trang 43 Tập 2 Cánh diều
Bài 8 trang 43 Toán 12 Tập 2: Một công trình xây dựng dự kiến hoàn thành trong 100 ngày. Số lượng công nhân được sử dụng tại thời điểm t cho bởi hàm số
m(t) = 500 + 50 – 10t,
trong đó t tính theo ngày (0 ≤ t ≤ 100), m(t) tính theo người.
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016)
a) Khi nào có 360 công nhân được sử dụng?
b) Khi nào số công nhân được sử dụng lớn nhất?
c) Gọi M(t) là số ngày công được tính đến hết ngày thứ t (kể từ khi khởi công công trình). Trong kinh tế xây dựng, người ta đã biết rằng M'(t) = m(t). Tổng cộng cần bao nhiêu ngày công để hoàn thành công trình xây dựng đó?
Lời giải:
a) Có 360 công nhân được sử dụng khi m(t) = 360, tức là
500 + 50 – 10t = 360 ⇔ 10t – 50 – 140 = 0 ⇒ = 7 ⇒ t = 49 ∈ [0; 100].
Vậy đến ngày thứ 49, có 360 công nhân được sử dụng.
b) Số công nhân được sử dụng lớn nhất chính là giá trị lớn nhất của hàm số m(t) trên đoạn [0; 100].
Ta có m'(t) = .
Trên khoảng (0; 100), m'(t) = 0 khi t = 6,25.
m(0) = 500; m(6,25) = 562,5; m(100) = 0.
Suy ra > khi t = 6,25.
Vậy đến ngày thứ 6 thì số lượng công nhân được sử dụng lớn nhất.
c) Số ngày công để hoàn thành công trình xây dựng đó là:
(ngày công).
Bài 9 trang 43 Toán 12 Tập 2: Trong bài này, ta xét một tình huống giả định có một học sinh sau kì nghỉ đã mang virus cúm quay trở lại khuôn viên trường học biệt lập. Sau khi có sự tiếp xúc giữa các học sinh, virus cúm lây lan trong khuôn viên trường. Giả thiết hệ thống chống dịch chưa được khởi động và virus cúm được lây lan tự nhiên. Gọi P(t) là số học sinh bị nhiễm virus cúm ở ngày thứ t tính từ ngày học sinh mang virus cúm quay trở lại khuôn viên trường. Biết rằng tốc độ lây lan của virus cúm cho bởi công thức P'(t) = – 0,02Ce– 0,02t, trong đó C là hằng số khác 0. Số học sinh bị nhiễm virus cúm sau 4 ngày là 55 học sinh. Xác định số học sinh bị nhiễm virus cúm sau 10 ngày.
Lời giải:
Hàm số P(t) là một nguyên hàm của hàm số P'(t).
Ta có .
Suy ra P(t) = – Ce– 0,02t + C1.
Với t = 0 thì P = 1, tức là P(0) = 0, suy ra – C + C1 = 1. (1)
Với t = 4 thì P = 55, tức là P(4), suy ra – Ce– 0,02 ∙ 4 + C1 = 55. (2)
Từ (1) và (2) suy ra C ≈ 702,36; C1 ≈ 703,36.
Vậy số học sinh bị nhiễm virus cúm sau 10 ngày là
P(10) = – 702,36e– 0,02 ∙ 10 + 703,36 ≈ 128 (học sinh).
Bài 10 trang 43 Toán 12 Tập 2: Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) lần lượt ở giây thứ 10, thứ 20, thứ 30, thứ 40, thứ 50 và thứ 60 được ghi lại trong Bảng 1.
|
Thời gian (giây) |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
Tốc độ (mét/giây) |
0 |
5 |
21 |
40 |
62 |
78 |
83 |
Bảng 1
a) Hãy xây dựng hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) để biểu diễn các số liệu ở Bảng 1, tức là ở hệ trục toạ độ Oxy, đồ thị của hàm số đó trên nửa khoảng [0; +∞) “gần” với các điểm O(0; 0), B(10; 5), C(20; 21), D(30; 40), E(40; 62), G(50; 78), K(60;83) (Nguồn: R. Larson and B. Edwards, Calculus 106, Cengage 2014).
b) Hãy tính (gần đúng) quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm.
Lời giải:
a) Hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) đi qua các điểm O(0; 0), B(10; 5), C(20; 21), D(30; 40) nên ta có hệ phương trình sau:
Vậy y = f(x) = (x ∈ [0; +∞)).
b) Gọi v(t) là tốc độ của chiếc xe ô tô đó với t tính bằng giây và v(t) tính bằng mét/giây.
Khi đó ta có .
Vậy quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm là:
(m)
Lời giải bài tập Toán 12 Bài tập cuối chương 4 hay khác:
Xem thêm lời giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 12 hay khác:
- Giải sgk Toán 12 Cánh diều
- Giải Chuyên đề học tập Toán 12 Cánh diều
- Giải SBT Toán 12 Cánh diều
- Giải lớp 12 Cánh diều (các môn học)
- Giải lớp 12 Kết nối tri thức (các môn học)
- Giải lớp 12 Chân trời sáng tạo (các môn học)
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

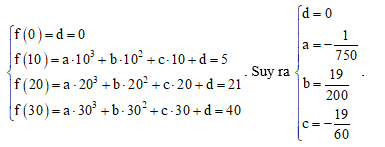



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

