Giải Toán 12 trang 22 Tập 2 Kết nối tri thức

Với Giải Toán 12 trang 22 Tập 2 trong Bài 13: Ứng dụng hình học của tích phân Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 22.

Giải Toán 12 trang 22 Tập 2 Kết nối tri thức

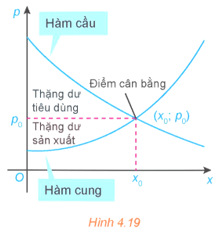
Vận dụng 1 trang 22 Toán 12 Tập 2: Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x₀; p₀) của đồ thị hàm cầu p = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p₀ và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p₀ và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R.Larson, Brief Calculus: An Applied Approach, 8^th edition, Cengage Learning, 2009).

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: p = −0,36x + 9 và hàm cung: p = 0,14x + 2, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Lời giải:

Hoành độ điểm cân bằng là nghiệm của phương trình:

−0,36x + 9 = 0,14x + 2 ⇔ x = 14.

Tọa độ điểm cân bằng là (14; 3,96).

Thặng dư tiêu dùng là:

$S_1=\underset{0}{\overset{14}{\int }}\left|-\mathrm{0,36}x+9-\mathrm{3,96}\right|dx$$=\underset{0}{\overset{14}{\int }}\left|-\mathrm{0,36}x+\mathrm{5,04}\right|dx$

$=\underset{0}{\overset{14}{\int }}\left(-\mathrm{0,36}x+\mathrm{5,04}\right)dx$

Thặng dư sản xuất là:

$S_2=\underset{0}{\overset{14}{\int }}\left|\mathrm{3,96}-\mathrm{0,14}x-2\right|dx$$=\underset{0}{\overset{14}{\int }}\left|\mathrm{1,96}-\mathrm{0,14}x\right|dx$

$=\underset{0}{\overset{14}{\int }}\left(\mathrm{1,96}-\mathrm{0,14}x\right)dx$$={\left.\left(\mathrm{1,96}x-\mathrm{0,07}{x}^2\right)\right|}_0^{14}$=13,72

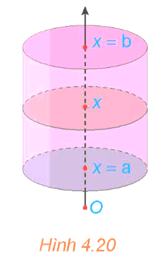
HĐ3 trang 22 Toán 12 Tập 2: Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20).

a) Tính thể tích V của hình trụ.

b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b). Từ đó tính $\underset{a}{\overset{b}{\int }}S\left(x\right)dx$ và so sánh với V.

Lời giải:

a) Độ dài chiều cao hình trụ là: h = b – a.

Thể tích của hình trụ là: V = πR²h = πR²(b – a).

b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox là

S(x) = πR².

Ta có $\underset{a}{\overset{b}{\int }}S\left(x\right)dx$$=\underset{a}{\overset{b}{\int }}\pi R^{2}dx$$={\left.\left(\pi R^{2}x\right)\right|}_a^b$$=\pi R^2\left(b-a\right)$

Vậy $V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$

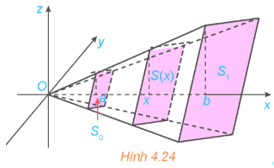
Vận dụng 2 trang 23 Toán 12 Tập 2: Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S₀, S₁ và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Lời giải:

Chọn hệ trục tọa độ Oxyz như hình vẽ.

Gọi a, b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn của hình chóp. Khi đó chiều cao của hình chóp cụt là h = b – a.

Thiết diện của khối chóp cụt khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b) là một đa giác đều đồng dạng với đáy lớn của hình chóp cụt theo tỉ số đồng dạng là $\frac{x}{b}$

Khi đó $\frac{S\left(x\right)}{S_1}=\frac{x^2}{b^2}\Rightarrow S\left(x\right)=\frac{x^2}{b^2}.S_1$

Do đó thể tích khối chóp cụt đều là:

$V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx=\underset{a}{\overset{b}{\int }}\frac{x^2}{b^2}{S}_{1}dx={\left.\frac{S_1}{b^2}.\frac{x^3}{3}\right|}_a^b$$=\frac{S_1}{3b^2}\left(b^3-a^3\right)$

$=\frac{b-a}{3b^2}.\left(S_1{b}^2+S_{1}ab+S_1{a}^2\right)$$=\frac{h}{3}.\left[S_1+S_1\frac{a}{b}+S_1{\left(\frac{a}{b}\right)}^2\right]$

Vì $\frac{S_0}{S_1}={\left(\frac{a}{b}\right)}^2\Rightarrow S_0=S_1.{\left(\frac{a}{b}\right)}^2$; $S_0{S}_1=S_1^2.{\left(\frac{a}{b}\right)}^2$$\Rightarrow \sqrt{S_0{S}_1}=S_1.\frac{a}{b}$

Do đó $V=\frac{h}{3}.\left[S_1+\sqrt{S_1.S_0}+S_0\right]$

Khối chóp đều được coi là khối chóp cụt đều khi S₀ = 0.

Do đó thể tích khối chóp đều là $V=\frac{1}{3}.S.h$

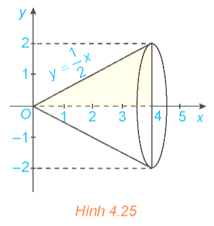
HĐ4 trang 24 Toán 12 Tập 2: Xét hình phẳng giới hạn bởi đồ thị hàm số $f\left(x\right)=\frac{1}{2}x$, trục hoành và hai đường thẳng x = 0, x = 4. Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).

a) Tính thể tích V của khối nón.

b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (0 ≤ x ≤ 4) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là S(x) = πf²(x). Tính $\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$ và so sánh với V.

Lời giải:

a) Ta có chiều cao của khối nón là h = 4, bán kính đáy của khối nón là R = 2.

Do đó thể tích của khối nón là $V=\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi {.2}^2.4=\frac{16\pi }{3}$

b)

Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (0 ≤ x ≤ 4) thì mặt cắt thu được là một hình tròn có bán kính là $f\left(x\right)=\frac{1}{2}x$

Khi đó diện tích mặt cắt là $S\left(x\right)=\pi f^2\left(x\right)=\frac{\pi }{4}{x}^2$

Ta có $\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$$=\pi \underset{0}{\overset{4}{\int }}\frac{x^2}{4}dx$$=\frac{\pi }{4}\underset{0}{\overset{4}{\int }}{x}^{2}dx$$={\left.\left(\frac{\pi }{4}.\frac{x^3}{3}\right)\right|}_0^4=\frac{16\pi }{3}$

Vậy $V=\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$

Lời giải bài tập Toán 12 Bài 13: Ứng dụng hình học của tích phân hay khác:

• Giải Toán 12 trang 20
• Giải Toán 12 trang 25
• Giải Toán 12 trang 26

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

• Toán 12 Bài tập cuối chương 4

• Toán 12 Bài 14: Phương trình mặt phẳng

• Toán 12 Bài 15: Phương trình đường thẳng trong không gian

• Toán 12 Bài 16: Công thức tính góc trong không gian

• Toán 12 Bài 17: Phương trình mặt cầu

Xem thêm các tài liệu học tốt lớp 12 hay khác:

• Giải sgk Toán 12 Kết nối tri thức
• Giải Chuyên đề học tập Toán 12 Kết nối tri thức
• Giải SBT Toán 12 Kết nối tri thức
• Giải lớp 12 Kết nối tri thức (các môn học)
• Giải lớp 12 Chân trời sáng tạo (các môn học)
• Giải lớp 12 Cánh diều (các môn học)

---