Giải Toán 12 trang 74 Tập 2 Kết nối tri thức

Với Giải Toán 12 trang 74 Tập 2 trong Bài 19: Công thức xác suất toàn phần và công thức Bayes Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 74.

Giải Toán 12 trang 74 Tập 2 Kết nối tri thức

Luyện tập 2 trang 74 Toán 12 Tập 2: Trở lại Ví dụ 1. Sử dụng sơ đồ hình cây, hãy mô tả cách tính xác suất để thứ Tư, ông An đi làm bằng xe buýt.

Lời giải:

Kí hiệu A là biến cố: “Thứ Ba, ông An đi làm bằng xe máy”; B là biến cố: “Thứ Tư, ông An đi làm bằng xe máy”.

Khi đó, biến cố “Thứ Tư, ông An đi làm bằng xe buýt” chính là $\overline{B}$.

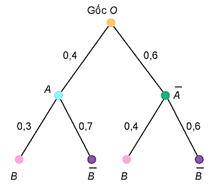
Ta có sơ đồ hình cây mô tả xác suất của biến cố như sau:

Hai nhánh cây đi tới $\overline{B}$ là $OA\overline{B}$ và $O\overline{A}\overline{B}$.

Như vậy $P\left(\overline{B}\right)$ = 0,4 ∙ 0,7 + 0,6 ∙ 0,6 = 0,64.

Vận dụng trang 74 Toán 12 Tập 2: Hình dạng hạt của đậu Hà Lan có hai kiểu hình: hạt trơn và hạt nhăn, có hai gene ứng với hai kiểu hình này là gene trội B và gene lặn b.

Khi cho lai hai cây đậu Hà Lan, cây con lấy ngẫu nhiên một cách độc lập một gene từ cây bố và một gene từ cây mẹ để hình thành một cặp gene. Giả sử cây bố và cây mẹ được chọn ngẫu nhiên từ một quần thể các cây đậu Hà Lan, ở đó tỉ lệ cây mang kiểu gene bb, Bb tương ứng là 40% và 60%. Tính xác suất để cây con có kiểu gene bb.

Lời giải:

Gọi A là biến cố: “Cây bố có kiểu gene bb”;

       M là biến cố: “Cây con lấy gene b từ cây bố”;

       N là biến cố: “Cây con lấy gene b từ cây mẹ”;

       E là biến cố: “Cây con có kiểu gene bb”.

Theo giả thiết, M và N độc lập nên P(E) = P(M) ∙ P(N).

Tính P(M): Ta áp dụng công thức xác suất toàn phần:

P(M) = P(A) ∙ P(M | A) + P($\overline{A}$) ∙ P(M | $\overline{A}$). (*)

Ta có P(A) = 0,4; P($\overline{A}$) = 0,6.

P(M | A) là xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene bb. Do đó, P(M | A) = 1.

P(M | $\overline{A}$) là xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene Bb. Do đó, P(M | $\overline{A}$) = 0,5.

Thay vào (*) ta được: P(M) = 0,4 ∙ 1 + 0,6 ∙ 0,5 = 0,7.

Tương tự tính được P(N) = 0,7.

Vậy P(E) = P(M) ∙ P(N) = 0,7 ∙ 0,7 = 0,49.

Từ kết quả trên suy ra trong một quần thể các cây đậu Hà Lan, mà ở đó tỉ lệ cây bố và cây mẹ mang kiểu gene bb, Bb tương ứng là 40% và 60%, thì tỉ lệ cây con có kiểu gene bb là khoảng 49%.

Luyện tập 3 trang 74 Toán 12 Tập 2: Với giả thiết như phần vận dụng:

Hình dạng hạt của đậu Hà Lan có hai kiểu hình: hạt trơn và hạt nhẵn, có hai gene ứng với hai kiểu hình này là gene trội B và gene lặn b.

Khi cho lai hai cây đậu Hà Lan, cây con lấy ngẫu nhiên một cách độc lập một gene từ cây bố và một gene từ cây mẹ để hình thành một cặp gene. Giả sử cây bố và cây mẹ được chọn ngẫu nhiên từ một quần thể các cây đậu Hà Lan, ở đó tỉ lệ cây mang kiểu gene bb, Bb tương ứng là 40% và 60%.

a) Hãy ước lượng tỉ lệ cây con có kiểu gene BB.

b) Sử dụng kết quả của vận dụng trên và câu a, hãy ước lượng tỉ lệ cây con có kiểu gene Bb.

Lời giải:

a) Gọi A là biến cố: “Cây bố có kiểu gene bb”;  

           K là biến cố: “Cây con nhận gene B từ bố”;

           H là biến cố: “Cây con nhận gene B từ mẹ”;

           F là biến cố: “Cây con có kiểu gene BB”.

Theo giả thiết, K và H độc lập nên P(F) = P(K) ∙ P(H).

Ta tính P(K) theo công thức xác suất toàn phần:

P(K) = P(A) ∙ P(K | A) + P($\overline{A}$) ∙ P(K | $\overline{A}$). (1)

Ta có P(A) = 0,4; P($\overline{A}$) = 0,6.

P(K | A) là xác suất để cây con nhận gene B từ bố với điều kiện bố có kiểu gene bb.

Vậy P(K | A) = 0.

P(K | $\overline{A}$) là xác suất để cây con nhận gene B từ bố với điều kiện bố có kiểu gene Bb.

Vậy P(K | $\overline{A}$) = 0,5.

Thay vào (2) ta được P(K) = 0,4 ∙ 0 + 0,6 ∙ 0,5 = 0,3.

Tương tự tính được P(H) = 0,3.

Vậy P(F) = P(K) ∙ P(H) = 0,3 ∙ 0,3 = 0,09.

Vậy tỉ lệ cây con có kiểu gene BB là khoảng 9%.

b) Gọi G là biến cố: “Cây con có kiểu gene Bb”.

Vì $\overline{G}=E\cup F$ và hai biến cố E, F xung khắc nên

P($\overline{G}$) = P(E) + P(F) = 0,49 + 0,09 = 0,58.

Vậy P(G) = 1 – P($\overline{G}$) = 1 – 0,58 = 0,42.

Vậy tỉ lệ cây con có kiểu gene Bb là khoảng 42%.

Lời giải bài tập Toán 12 Bài 19: Công thức xác suất toàn phần và công thức Bayes hay khác:

• Giải Toán 12 trang 77
• Giải Toán 12 trang 78

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

• Toán 12 Bài tập cuối chương 5

• Toán 12 Bài 18: Xác suất có điều kiện

• Toán 12 Bài tập cuối chương 6

• Toán 12 Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang

• Toán 12 Vẽ đồ hoạ 3D với phần mềm GeoGebra

Xem thêm các tài liệu học tốt lớp 12 hay khác:

• Giải sgk Toán 12 Kết nối tri thức
• Giải Chuyên đề học tập Toán 12 Kết nối tri thức
• Giải SBT Toán 12 Kết nối tri thức
• Giải lớp 12 Kết nối tri thức (các môn học)
• Giải lớp 12 Chân trời sáng tạo (các môn học)
• Giải lớp 12 Cánh diều (các môn học)

---