Đề thi Giữa kì 2 Toán lớp 10 năm 2024 có ma trận (8 đề)

Đề thi Giữa kì 2 Toán lớp 10 năm 2024 có ma trận (8 đề)

Với Đề thi Giữa kì 2 Toán lớp 10 năm 2024 có ma trận (8 đề), chọn lọc giúp học sinh ôn tập và đạt kết quả cao trong bài thi Giữa kì 2 Toán 10.

A. MA TRẬN

Nội dung kiến thức	Mức độ nhận thức								Tổng			% tổng điểm
	Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao		Số CH		Thời gian (phút)
	Số CH	Thời gian (phút)	Số CH	Thời gian (phút)	Số CH	Thời gian (phút)	Số CH	Thời gian (phút)	TN	TL
Bất đẳng thức	2	2	2	4	1	8	1*	12	4	2	53	61
Bất phương trình và hệ bất phương trình một ẩn	4	4	2	4			0		6
Dấu của nhị thức bậc nhất	2	2	2	4			1*		4
Bất phương trình bậc nhất hai ẩn	2	2	1	2			0		3
Dấu của tam thức bậc hai	3	3	3	6			1*		6
Hệ thức lượng trong tam giác	3	3	2	4	1	8	1	12	5	2	37	39
Phương trình đường thẳng	4	4	3	6					7
Tổng	20	20	15	30	2	16	2	24	35	4	90
Tỉ lệ (%)	40		30		20		10					100
Tỉ lệ chung (%)	70				30							100

B. ĐỀ THI

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 1)

I. PHẦN TRẮC NGHIỆM

Câu 1: Cho các số thực a, b thỏa mãn a < b. Mệnh đề nào dưới đây đúng ?

A. ac < bc với mọi c ≤ 0                             

B. ac < bc với mọi c ≥ 0

C. ac < bc với mọi c < 0                            

D. ac < bc với mọi c > 0

Câu 2: Với các số thực không âm a, b tùy ý, mệnh đề nào dưới đây đúng ?

A. a + b ≥ 5√ab                                

B. a + b ≥ 2√ab

C. a + b ≥ 3√ab                                

D. a + b ≥ 4√ab

Câu 3: Điều kiện xác định của bất phương trình là 

A. x ≠ 2              

B. x ≥ 2               

C. x ≤ 2               

D. x = 2

Câu 4: Trong các số dưới đây, số nào là nghiệm của bất phương trình x² ≥ 4x

A. 4                     

B. 1                     

C. 2                     

D. 3

Câu 5: Tập nghiệm của hệ bất phương trình 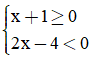 là

A. [-1; 2]             

B. [-1; 2)             

C. (-1; 2]             

D. (-1; 2)

Câu 6: Tập nghiệm của bất phương trình 2x ≥ -6 là

A. (-∞: -3]                  

B. (-3; +∞)                  

C. [-3; +∞)                  

D. (-∞: -3)

Câu 7: Nhị thức bậc nhất nào dưới đây có bảng xét dấu như sau

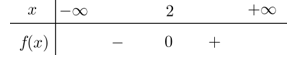
A. f(x) = 2x - 4  

B. f(x) = -2x + 4         

C. f(x) = -x + 2

D. f(x) = x + 2

Câu 8: Tập nghiệm của bất phương trình (3 - x)(x + 2) > 0 là

A. [-3; 2]              

B. (-2; 3]             

C. (-3; 2)            

D. (-2; 3)

Câu 9: Cặp số (x; y) nào dưới đây là nghiệm của bất phương trình 2x - y - 3 > 0

A. (1; 0)                

B. (2; 2)               

C. (2; -1)             

D. (0; 2)

Câu 10: Trong mặt phẳng Oxy điểm nào dưới đây thuộc miền nghiệm của hệ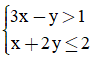

A. P(-1; 0)           

B. N(1; 1)             

C. M(1; -1)                   

D. Q(0; 1)

Câu 11: Cho tam thức bậc hai f(x) = 2x² - x - 2. Giá trị f(-1) bằng

A. -2                           

B. -1                            

C. 3                     

D. 1

Câu 12: Cho tam thức bậc hai f(x) = x² - 4x + 4. Mệnh đề nào dưới đây đúng ?

A. f(x) > 0, ∀x ∈ R                                    

B. f(x) ≥ 0, ∀x ∈ R

C. f(x) < 0, ∀x ∈ R                                    

D. f(x) ≤ 0, ∀x ∈ R

Câu 13: Cho tam thức bậc hai có bảng xét dấu như sau

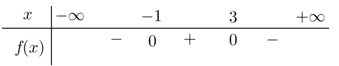
Mệnh đề nào dưới đây đúng ?

A. f(x) ≥ 0 ⇔ -1 ≤ x ≤ 3                           

B. f(x) ≥ 0 ⇔ x < 3

C. f(x) ≥ 0 ⇔ x > 3                                    

D. f(x) ≥ 0 ⇔ x < -1

Câu 14: Xét tam giác ABC tùy ý có BC = a, AC = b, AB = c. Mệnh đề nào dưới đây đúng ?

A. a² = b² + c² + 2bc.cosA                         

B. a² = b² + c² - 2bc.cosA

C. a² = b² + c² - bc.cosA                           

D. a² = b² + c² + bc.cosA

Câu 15: Xét tam giác ABC tùy ý, đường tròn ngoại tiếp tam giác có bán kính R, BC = a. Mệnh đề nào dưới đây đúng ?

Câu 16: Xét tam giác ABC tùy ý có BC = a, AC = b, AB = c. Diện tích của tam giác ABC bằng

Câu 17: Trong mặt phẳng Oxy cho đường thẳng 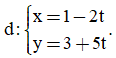 Vectơ nào dưới đây là một vectơ chỉ phương của d

Câu 18: Trong mặt phẳng Oxy, đường thẳng nào dưới đây đi qua gốc tọa độ ?

A. d₄: y + 1 = 0    

B. d₂: x + y - 1 = 0       

C. d₃: 2x - 3 = 0  

D. d₁: 2x + y = 0

Câu 19: Trong mặt phẳng Oxy, xét hai đường thẳng tùy ý d₁: a₁x + b₁y + c₁ = 0 và d₁: a₂x + b₂y + c₂ = 0. Đường thẳng d₁ vuông góc với đường thẳng d₂ khi và chỉ khi

A. a₁a₂ - b₁b₂ = 0

B. a₁a₂ + b₁b₂ = 0

C. a₁b₂ + a₂b₁ = 0

D. a₁b₂ - a₂b₁ = 0

Câu 20: Trong mặt phẳng Oxy cho đường thẳng d: 3x - 2y + 1 = 0 Vectơ nào dưới đây là một vectơ pháp tuyến của d

Câu 21: Với các số thực a, b tùy ý, mệnh đề nào dưới đây đúng? 

Câu 22: Trong tất cả các hình chữ nhật có cùng chu vi bằng 40, gọi H là hình có diện tích lớn nhất. Diện tích của H bằng

A. 50                   

B. 400        

C. 100        

D. 200

Câu 23: Bất phương trình nào dưới đây tương đương với bất phương trình 2x ≥ x - 2 ?

Câu 24: Số nghiệm nguyên của bất phương trình 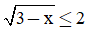 là

A. 4                      

B. 3                     

C. 5                     

D. 6

Câu 25: Cho nhị thức f(x) = -2x + 1. Tập hợp tất cả các giá trị x để f(x) ≥ 0 là

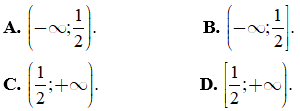
Câu 26: Cho nhị thức f(x) = 2x - m. Tìm tất cả các giá trị thực của tham số m để f(x) > 0 với mọi x > 1.

A. m < 2             

B. m ≤ 1              

C. m ≤ 2              

D. m < 1

Câu 27: Trong mặt phẳng Oxy phần nửa mặt phẳng gạch chéo (kể cả bờ) trong hình vẽ dưới đây là biểu diễn hình học tập nghiệm của bất phương trình nào ?

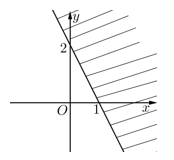
A. x + 2y ≥ 2                

B. 2x + y ≤ 2                

C. x + 2y ≤ 2                

D. 2x + y ≥ 2

Câu 28: Tập nghiệm của bất phương trình x² - 4x - 5 ≤ 0 là

A. S = (-1; 5)                                             

B. S = [-1; 5]

C. S = (-∞; -1] ∪ [5; +∞)                          

D. S = (-∞; -1) ∪ (5; +∞)

Câu 29: Xét tam thức bậc hai f(x) = ax² + bx + c có Δ = b² - 4ac. Khi đó f(x) < 0, ∀x ∈ R khi và chỉ khi

Câu 30: Tìm tất cả các giá trị thực của tham số m để phương trình 2x² - 3x + m² - m = 0 có hai nghiệm trái dấu.

A. m < 0              

B. 0 ≤ m ≤ 1                  

C. m > 1              

D. 0 < m < 1

Câu 31: Cho tam giác ABC, đường tròn ngoại tiếp tam giác có bán kính bằng 25cm, ∠BAC = 70⁰. Tính độ dài cạnh BC (kết quả làm tròn đến hàng đơn vị) ?

A. BC = 39cm     

B. BC = 23cm     

C. BC = 47cm     

D. BC = 19cm

Câu 32: Cho tam giác ABC có diện tích bằng 6 và chu vi bằng 12. Bán kính đường tròn nội tiếp của tam giác ABC bằng

Câu 33: Trong mặt phẳng Oxy, cho điểm A(-1; 1) và đường thẳng d: x - 2y + 1 = 0. Phương trình đường thẳng đi qua A và vuông góc với d là

A. 2x + y - 1 = 0

B. x + 2y - 1 = 0

C. 2x - y + 3 = 0

D. 2x + y + 1 = 0

Câu 34: Trong mặt phẳng Oxy cho điểm M(1; 1) và đường thẳng d: 3x + 4y + 2 = 0. Khoảng cách từ M đến d bằng

Câu 35: Trong mặt phẳng Oxy cho hai đường thẳng d₁: x + y + 2 = 0 và d₂: 2x - 3 = 0. Góc giữa hai đường thẳng d₁ và d₂ bằng

A. 60⁰                 

B. 30⁰                 

C. 45⁰                 

D. 90⁰

PHẦN TỰ LUẬN

Câu 1: Tìm tất cả các giá trị thực của tham số m để  bất phương trình sau vô nghiệm.

(m - 4)x² + (m + 1)x + 2m - 1 > 0

Câu 2: Trong mặt phẳng Oxy cho điểm A(1; 2). Viết phương trình đường thẳng đi qua A cắt hai trục Ox, Oy lần lượt tại M và N ( khác O) thỏa mãn ON = 2OM

Câu 3: Hai chiếc tàu thủy P và Q trên biển cách nhau 100m và thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển. Từ P và Q người ta nhìn chiều cao AB của tháp dưới các góc ∠BPA = 15⁰ và ∠BQA = 55⁰. Tính chiều cao của tháp (kết quả làm tròn đến hàng đơn vị).

                             

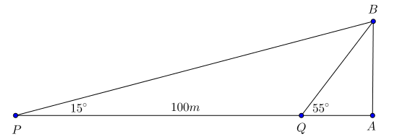
Câu 4: Cho a, b , c là độ dài ba cạnh của một tam giác. Chứng minh rằng a² + b² + c² < 2(ab + bc + ca)

                                            

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 2)

PHẦN I: TRẮC NGHIỆM(5,0 điểm)

Câu 1. Cho tam giác ABC có A(-4; 1), B(6; 4), C(2; -2). Phương trình đường cao AH của tam giác ABC là

A. 4x - y + 5 = 0.      

B. 2x - 3y + 5 = 0.     

C. 4x + y + 5 = 0.      

D. 2x + 3y + 5 = 0. 

Câu 2. Điểm A(-4; 3) là điểm thuộc miền nghiệm của bất phương trình nào dưới đây ?

A. x - 3y + 5 ≥ 0      

B. -2x + 3y - 5 > 0

C. x - 2y - 1 < 0      

D. 3x + 5y + 21 ≤ 0

Câu 3. Cho f(x) = -2x + 6 chọn mệnh đề đúng trong các mệnh đề sau

A. f(x) < 0 ⇔ x < 3  

B. f(x) > 0 ⇔ x > 3   

C. f(x) > 0 ⇔ x < 3  

D. f(x) > 0 ⇔ x > 2

Câu 4. Số nghiệm nguyên âm của bất phương trình 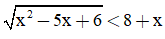 là

A. 0                          

B. 2                           

C. 3                           

D. 1.

Câu 5. Vectơ pháp tuyến của đường thẳng x - 3y + 4 = 0 là

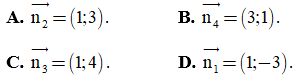
Câu 6. Tập nghiệm của bất phương trình x² - 4x - 12 < 0 là

A. (-2; 6)                   

B. (-∞; -2) ∪ (6; +∞)                                 

C. (6; +∞)                 

D. (-∞; -2)

Câu 7. Trong tam giác ABC, hệ thức nào sau đây sai?

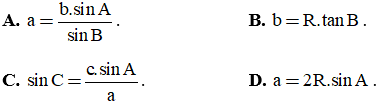
Câu 8. Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Điều kiện của a và Δ = b² - 4ac để f(x) > 0, ∀x ∈ R là

Câu 9. Bất phương trình 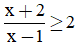 có tập nghiệm là

A. [1; 4)                      

B. (-∞; 1) ∪ [4; +∞)

C. [1; 4]                      

D. (1; 4]

Câu 10. Tam giác ABC có AB = 12, AC = 13, ∠A = 30⁰. Tính diện tích tam giác ABC.

A. 39√3.                    

B. 39.                         

C. 78.                        

D. 78√3.

Câu 11. Tìm m để phương trình x² - (m - 3)x + 3 - 2m = 0 (m là tham số) có nghiệm.

Câu 12. Tam giác ABC có BC = 5√5, AC = 5√2, AB = 5. Tính ∠BAC.

A. 135⁰.                     

B. 30⁰.                       

C. 45⁰.                       

D. 120⁰.

Câu 13. Cho x, y là các số thực thỏa mãn 5x² + 2xy + 2y² = 9. Giá trị nhỏ nhất của 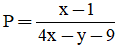 bằng

Câu 14. Bất phương trình |2x + 1| ≤ 3 có tập nghiệm là

A. (-∞; -2] ∪ [1; +∞)                                  

B. [-2; 1]                    

C. [-2; 1)                   

D. (-2; 1]

Câu 15. Hệ bất phương trình 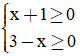 có tập nghiệm là

A. [-1; 3]                   

B. (-1; 3]                   

C. [-1; 3)                   

D. (-∞; -1] ∪ [3; +∞)

Câu 16. Cho tam giác ABC có AB + AC = 13, ∠A = 60⁰, bán kính đường tròn nội tiếp tam giác bằng √3. Tính độ dài cạnh BC.

A. 7                            

B. 2√33.                      

C. 6,5.                        

D. 3√2.

Câu 17. Vectơ chỉ phương của đường thẳng 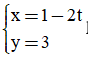 là

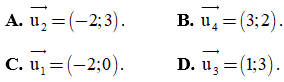
Câu 18. Tập nghiệm của bất phương trình x - 5 < 7 - 3x là

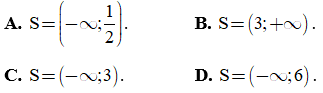
Câu 19. Bất phương trình -2x + 5 ≤  có tập nghiệm là

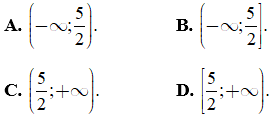
Câu 20. Cho biểu thức: f(x) = (-2x + 4)(x + 3)(x - 1) nhận giá trị dương khi và chỉ khi

Câu 21. Hệ bất phương trình 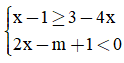 có nghiệm khi

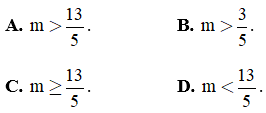
Câu 22. Tìm m để f(x) = (m - 1)x + 1 - 2m là nhị thức bậc nhất

A. m > 1                    

B. m < 1                    

C. m = 1                   

D. m ≠ 1

Câu 23. Cho hệ bất phương trình 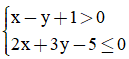 điểm nào sau đây thuộc miền nghiệm của hệ?

A. (5; 1).                      

B. (3; 1).                      

C. (-4; 2).                  

D. (1; -2). 

Câu 24. Bất phương trình (x - 2)(3 - x) ≥ 0 có tập nghiệm là

A. [2; 3]                       

B. (2; 3)                     

C. [3; +∞)                

D. (-∞; 2]

Câu 25. Cho tam giác ABC, đường tròn ngoại tiếp tam giác có bán kính bằng 25cm, ∠BAC = 70⁰. Tính độ dài cạnh BC (kết quả làm tròn đến hàng đơn vị) ?

A. BC = 39cm     

B. BC = 23cm     

C. BC = 47cm     

D. BC = 19cm

PHẦN II: TỰ LUẬN (5,0 điểm)

Câu 1: Giải bất phương trình sau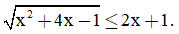

Câu 2: Tìm tất cả các giá trị thực của tham số m để bất phương trình mx² + 2mx - 3 < 0 nghiệm đúng với mọi số thực x

Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(2; 1), B(0; -3) và đường thẳng d: -x + 2y - 3 = 0.

a) Hãy lập phương trình đường thẳng Δ đi qua hai điểm A, B

b) Tìm tọa độ điểm C thuộc đường thẳng d sao cho ba điểm A, B, C tạo thành một tam giác vuông tại đỉnh C.

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 3)

Câu 1: Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Mệnh đề nào sau đây đúng?

A. Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số b, với mọi x ∈ R.

B. Nếu Δ > 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ R.

C. Nếu Δ < 0 thì f(x) luôn trái dấu với hệ số a, với mọi x ∈ R.

D. Nếu Δ = 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ R\.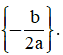

Câu 2: Bất phương trình 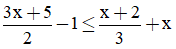 có bao nhiêu nghiệm nguyên lớn hơn -10 ?

A. 4.                            

B. 10.                           

C. 5.                            

D. 9.

Câu 3: Cho biểu thức 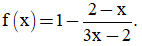Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 là

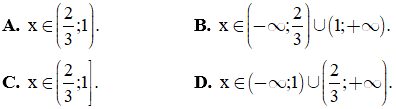
Câu 4: Tập nghiệm của bất phương trình 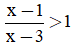 là

A. (3; +∞).                     

B. R.                                                            

C. (-∞; 3).                                                   

D. (-∞; 3) ∪ (3; +∞)

Câu 5: Cho mẫu số liệu {10; 8; 6; 2; 4}.Độ lệch chuẩn của mẫu là:

A. 8                             

B. 2,4                           

C. 2,8                          

D. 6

Câu 6: Cho điểm M(x₀, y₀) và đường thẳng (Δ): ax + by + c = 0. Khi đó khoảng cách d(M; (Δ)) là:

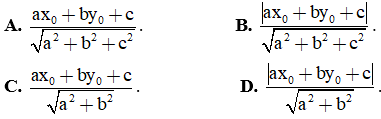
Câu 7: Biết rằng tập nghiệm của bất phương trình 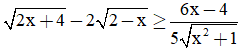 là [a; b]. Khi đó P = 3a - 2b bằng:

A. 4                            

B. 2                            

C. 1                            

D. -2

Câu 8: Tập nghiệm của bất phương trình (x - 3)(x² + x - 6) > (x - 2)(x² + 5x + 4) có dạng (a; b) với a, b ∈ R. Giá trị của a + b là

Câu 9: Bất phương trình -x² + 2x + 3 > 0 có tập nghiệm là

A. (-∞; -1) ∪ (3; +∞)

B. [-1; 3].                                                      

C. (-1; 3).                                                             

D. (-3; 1).

Câu 10: Hàm số có kết quả xét dấu sau là hàm số nào?

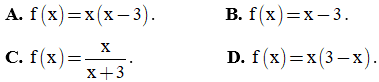
Câu 11: Cho tam giác ABC, có độ dài ba cạnh là BC = a, AC = b, AB = c. Gọi m_a là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây sai?

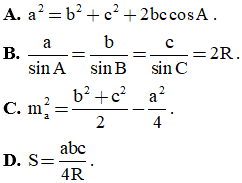
             Câu 12: Cho hàm số y = f(x) = ax² + bx + c có đồ thị như hình vẽ. 

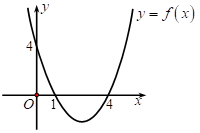
             Đặt Δ = b² - 4ac, tìm dấu của a và Δ.

A. a < 0, Δ = 0.        

B. a > 0, Δ .> 0.          

C. a > 0, Δ = 0.          

D. a < 0, Δ > 0.

Câu 13: Điểm thi học kì của một học sinh như sau: 4;6;2;7;3;5;9;8;7;10;9. Số trung bình và số trung vị lần lượt là

A. 7 và 6                      

B. 6,(36) và 7               

C. 6,22 và 7                 

D. 6 và 6

Câu 14: Cặp số (1; -1) là nghiệm của bất phương trình:

A. x + 4y < 1

B. x + y - 2 > 0                                           

C. -x - 3y - 1 < 0

D. -x - y < 0

Câu 15: Biểu diễn miền nghiệm được cho bởi hình bên là miền nghiệm của bất phương trình nào ?

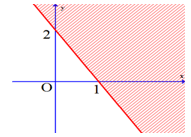
A. 2x + y - 2 ≤ 0        

B. 2x + y - 2 > 0        

C. 2x + y - 1 > 0         

D. 2x + y + 2 ≤ 0

Câu 16: Tập nghiệm của bất phương trình là

A. (-∞; 2021).            

B. .                   

C. [2021, +∞).             

D. ∅.

Câu 17: Tâm và bán kính của đường tròn (x - 4)² + (y + 2)² =  25 là:

A. I(4; 2), R = 5                                             

B. I(4; -2), R = 25

C. I(4; -2), R = 5                                          

D. I(-4; 2), R = 5

Câu 18: Điều kiện xác định của bất phương trình 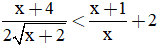 là

A. x ∈ (-2; +∞)                                           

B. x ∈ (2; +∞) 

C. x ∈ (-2; 0) ∪ (0; +∞)                                 

D. x ∈ R\{0}

Câu 19: Cho f(x) = 2x - 4, khẳng định nào sau đây là đúng?

A. f(x) > 0 ⇔ x ∈ (-2; +∞)                        

B. f(x) < 0 ⇔ x ∈ (-∞; -2)

C. f(x) > 0 ⇔ x ∈ (2; +∞).                           

D. f(x) = 0 ⇔ x = -2.

Câu 20: Tìm m để biểu thức f(x) = (2m - 1)x² + 4x + m là một tam thức bậc hai

Câu 21: Đường tròn (C) đi qua hai điểm A(-1; 2), B(-2; 3) và có tâm I thuộc đường thẳng (Δ): 3x - y + 10 = 0 là:

A. (x + 3)² + (y - 1)² = √5

B. (x - 3)² + (y + 1)² = √5 .

C. (x - 3)² + (y + 1)² = 5 .                               

D. (x + 3)² + (y - 1)² = 5 .

Câu 22: Trong các biểu thức sau, đâu là nhị thức bậc nhất  :

A. f(x) = -3x + 2                                        

B. f(x) = 3x² + 2x - 1

C. f(x) = 2mx + 1                                         

D. f(x) = |4x - 5|

Câu 23: Cho hai đường thẳng d₁: 2x + 5y - 2= 0 và d₂: 3x - 7y + 3 = 0. Góc tạo bởi đường thẳng d₁ và d₂ bằng

A. 135⁰.                       

B. 45⁰.                         

C. 30⁰.                         

D. 60⁰.

Câu 24: Tìm tất cả các giá trị của tham số m để hàm số 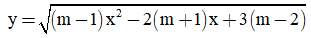 có tập xác định

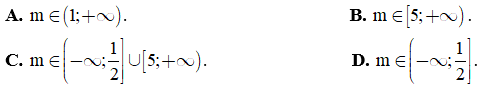
Câu 25: Trong mặt phẳng với hệ trục tọa độ Oxy, cho ΔABC có A(1; -1), B(-2; 1), C(3; 5). Diện tích ΔABK với K là trung điểm của AC là

A. S_ΔABK = 11/2 (đvdt)      

B. S_ΔABK = 5 (đvdt)             

C. S_ΔABK = 11 (đvdt)                        

D. S_ΔABK = 10 (đvdt)

Câu 26: Cho bảng xét dấu

Hỏi bảng xét dấu trên của tam thức nào sau đây:

A. f(x) = -x² + 5x - 6

B. f(x) = x² - 5x + 6   

C. f(x) = x² + 5x - 6

D. f(x) = -x² + 5x + 6

Câu 27: Cho tam giác ABC có BC = 5cM, CA = 12cm, AB = 13cm.Bán kính đường tròn nội tiếp tam giác ABC bằng

A. 1                             

B. 2                            

C. 3                            

D. 3,5

             Câu 28: Cho nhị thức f(x) = x - 1. Mệnh đề nào sau đây đúng?

A. f(x) < 0 ⇔ x ≥ 1.       

B. f(x) < 0 ⇔ x ≤ 1 .       

C. f(x) < 0 ⇔ x > 1 .                

D. f(x) < 0 ⇔ x < 1 .

Câu 29: Tập nghiệm của hệ bất phương trình 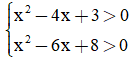 là

A. (-∞; 1) ∪ (4; +∞).                                    

B. (-∞; 1) ∪ (3; +∞).  

C. (-∞; 2) ∪ (3; +∞).                                   

D. (1; 4).

Câu 30: Phương trình tham số của đường thẳng qua M(1; -2), N(4; 3) là

Câu 31: Tìm tất cả các giá trị của tham số m để tam thức bậc hai f(x) sau đây thỏa mãn f(x) = -x² + 2x + m - 2022 < 0, ∀x ∈ R.

A. m > 2022.               

B. m < 2021.               

C. m > 2021.               

D. m < 2020.

Câu 32: Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng (Δ): 3x - 4y + 1 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng (Δ)?

A. (4; 3).                      

B. (3; -4).                    

C. (4; -3).                   

D. (3; 4).

Câu 33: Tập nghiệm của bất phương trình 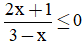 được biểu diễn dạng (-∞; a] ∪ (b; +∞) với a, b là các số hữu tỉ. Giá trị của biểu thức 2a + b có thể bằng

A. 2.                            

B. 3.                             

C. 4.                            

D. –2.

Câu 34: Bất phương trình 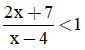 có bao nhiêu nghiệm nguyên dương?

A. 0.                            

B. 114.                          

C. 4                           

D. 3.

Câu 35: Trong mặt phẳng tọa độ với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm H(1; 2) là hình chiếu vuông góc của A lên BD. Điểm 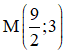là trung điểm cạnh BC. Phương trình đường trung tuyến kẻ từ đỉnh A của tam giác ADH là 4x + y - 4 = 0. Biết điểm D có tọa độ (x_D, y_D) là tính giá trị biểu thức S = 4x_D² + y_D².

A. S = 3.                      

B. S = 4.                      

C. S = 6.                      

D. S = 5

Câu 36: Tìm tất cả các giá trị của tham số m để phương trình mx² + 2x + m² + 2m + 1 = 0 có hai nghiệm trái dấu.

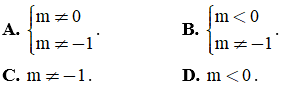
Câu 37: Tìm m để f(x) = (m – 2)x + 2m – 1 là nhị thức bậc nhất.

A. .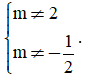               

B. m > 2.                      

C. m < 2.                      

D. m ≠ 2.

Câu 38: Bảng xét dấu sau là của biểu thức nào?

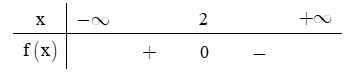
A. f(x) =  x - 2.   

B. f(x) =  2 - 4x.  

C. f(x) =  16 - 8x. 

D. f(x) =  -x - 2.

Câu 39: Cho đường thẳng d: 3x + 5y + 2018 = 0. Tìm mệnh đề sai trong các mệnh đề sau:

A. d có vectơ pháp tuyến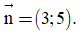    

B. d có vectơ chỉ phương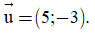

C. d có hệ số góc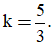                    

D. d song song với đường thẳng Δ: 3x + 5y = 0

Câu 40: Cho phương trình x² + y² + 2mx + 2(m - 1)y + 2m² = 0 (1). Tìm điều kiện của m để (1) là phương trình đường tròn.

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 4)

I. PHẦN TRẮC NGHIỆM

Câu 1. Gọi S = m_a² + m_b² + m_c² là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng?

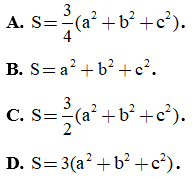
Câu 2. Cho tam giác ABC, có độ dài ba cạnh là BC = a, AC = b, AB = c. Gọi m_a là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây sai?

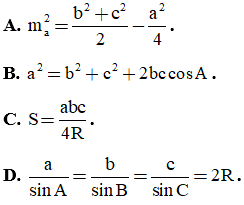
Câu 3. Tập nghiệm của bất phương trình 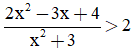 là

Câu 4. Tập nghiệm của bất phương trình 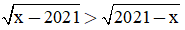 là

A. [2021; +∞).                      

B. (-∞; 2021).                      

C. {2021} .                             

D. ∅.

Câu 5. Số nghiệm nguyên dương của bất phương trình (2 - x)(x + 1)(3 - x) ≤ 0 là

A. 1.                                      

B. 4.                                     

C. 2.                                     

D. 3.

Câu 6. Điều kiện xác định của bất phương trình 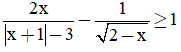 là

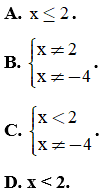
Câu 7. Cho a là số thực dương. Mệnh đề nào dưới đây đúng?

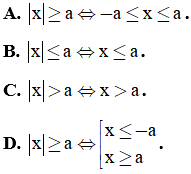
Câu 8. Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D

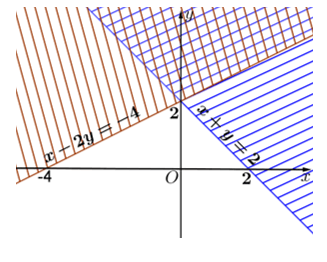
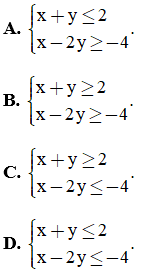
Câu 9. Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. x - 5y + 3z ≤ 0.              

B. 3x² + 2y - 4 > 0.              

C. 3x² + 5y > 3.                    

D. 2x + 3y < 5.

Câu 10. Bảng xét dấu sau là của biểu thức nào?

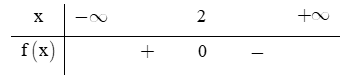
A. f(x) = x - 2.                    

B. f(x) = 2 - 4x.                  

C. f(x) = 16 - 8x.                 

D. f(x) = -x - 2

Câu 11. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x + y < 1?

A. (-2 ; 1).                             

B. (3; -7).                             

C. (0; 1).                                

D. (0; 0).

Câu 12. Tập nghiệm của bất phương trình -x² + x + 12 ≥ 0 là

A. (-∞; -3] ∪ [4; +∞).                                      

B. ∅.

C. (-∞; -4] ∪ [3; +∞).                                      

D. [-3; 4].

Câu 13. Tam giác ABC có A = 120⁰ thì câu nào sau đây đúng?

A. a² = b² + c² – 3bc.                                             

B. a² = b² + c² + bc. 

C. a² = b² + c² + 3bc .                                             

D. a² = b² + c² – bc . 

Câu 14. Cho tam giác ABC thoả mãn: b² + c² – a² = √3bc. Khi đó:

A. ∠A = 30⁰                         

B. ∠A = 45⁰                            

C. ∠A = 60⁰                            

D. ∠A = 75⁰.

Câu 15. Tập nghiệm của bất phương trình 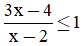 là:

A. S = (1; 2].                                                        

B. S = [1; 2].                          

C. S = [1; 2).                                                         

D. S = (-∞; 1] ∪ (2; +∞].

Câu 16. Trong hệ trục tọa độ Oxy, Véctơ nào là một véctơ pháp tuyến của đường thẳng ?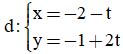

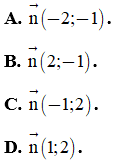
Câu 17. Tập xác định của hàm số 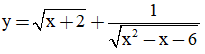 là:

A. D = (-2; +∞)                 

B. D = (-2; 3)                      

C. D = (3; +∞)                    

D. D = (-∞; -2]

Câu 18. Viết phương trình chính tắc của đường thẳng Δ đi qua M(1; -3) và nhận vectơ 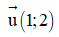 làm vectơ chỉ phương.

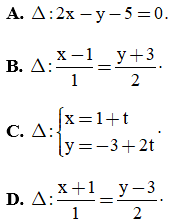
Câu 19. Tìm giá trị của tham số m để phương trình x² - (m - 2)x + m² - 4m = 0 có hai nghiệm trái dấu.

A. 0< m < 4.                        

B. m < 0 hoặc m > 4.           

C. m > 2.                              

D. m < 2.

Câu 20. Cho x² + y² = 1, gọi S = x + y. Khi đó ta có

A. S ≤ √2.                            

B. S ≥ √2.                             

C. -√2 ≤ S ≤ √2.                 

D. -1 ≤ S ≤ 1.

Câu 21. Tập nghiệm của bất phương trình |2x - 4| ≤ x + 12 là:

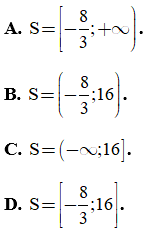
Câu 22. Bất phương trình: |3x - 2|(x² + 1) ≥ 0 có tập nghiệm là:

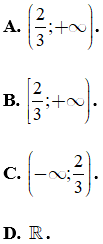
Câu 23. Cho tam giác ABC, các đường cao h_a, h_b; h_c thỏa mãn hệ thức 3h_a = 2h_b + h_c. Tìm hệ thức giữa a, b, .

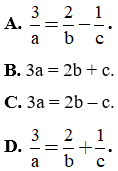
Câu 24. Cho đường thẳng Δ: x - y + 3 = 0. Véc tơ nào sau đây không là véc tơ chỉ phương của Δ?

Câu 25. Giải bất phương trình |x + 1| + |x - 4| > 7. Giá trị nghiệm nguyên dương nhỏ nhất của x thoả bất phương trình là

A. x = 9.                                

B. x = 8.                                

C. x = 7.                                

D. x = 6.

Câu 26. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d cắt hai trục Ox, Oy lần lượt tại hai điểm A(a; 0), B(0; b), (a, b ≠ 0). Viết phương trình đường thẳng d.

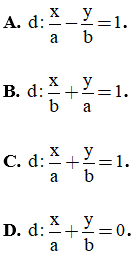
Câu 27. Với giá trị nào của m thì 2 đường thẳng sau đây vuông góc?

Δ₁: (2m - 1)x + my - 10 = 0 và Δ₂: 3x + 2y + 6 = 0

A. m = 0.                              

B. m ∈ ∅.                              

C. m = 2.                               

D. m = 3/8

Câu 28. Nghiệm của bất phương trình 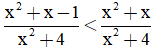 là:

A. x > 1.                                

B. x < 1.                                

C. x > 4.                                

D. x ∈ R

Câu 29. Cho các bất đẳng thức a > b và c > d. Bất đẳng thức nào sau đây đúng

A. a – c > b – d 

B. a + c > b + d                      

C. ac > bd                              

D.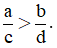

Câu 30. Phương trình của đường thẳng qua A(1; 4) và cách B(-3; 1) một khoảng bằng 3 là:

A. 24x + 7y – 52 = 0.                                           

B. x = 4, y = 4.

C. y = 4, 24x – 7y + 4 = 0.      

D. x = 4, 24x + 7y – 52 = 0.

PHẦN TỰ LUẬN

Bài 1. (1,0 điểm) Giải bất phương trình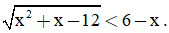

Bài 2(1 điểm). Một tam giác có ba cạnh là 52, 56, 60. Tính bán kính đường tròn ngoại tiếp tam giác.

Bài 3. (1,5 điểm) 

a) Trong mặt phẳng với hệ tọa độ Oxy, cho đường thằng d: 3x - 4y + 1 = 0. Tìm tọa độ điểm M trên trục Ox sao cho điểm M cách đường thẳng d một khoảng bằng 2.

b) Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(0; 1) và đường thẳng 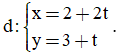 Tìm điểm M thuộc d và cách A một khoảng bằng 5, biết M có hoành độ âm.

Bài 4. (0,5 điểm) Chứng minh rằng ∀x, y ∈ R ta có: x² + y² + xy + x + y + 1 ≥ 0.

Sở Giáo dục và Đào tạo .....

Đề thi Giữa kì 2

Năm học 2024 - 2025

Bài thi môn: Toán lớp 10

Thời gian làm bài: phút

(không kể thời gian phát đề)

(Đề số 5)

I. TRẮC NGHIỆM (35 câu – 7 điểm)

Câu 1. Biểu thức nào dưới đây là nhị thức bậc nhất?

A. f(x) = 2x + 1   

B. f(x) = 2          

C. f(x) = 4x²

D. f(x) = 5 - x³

Câu 2. Cho a, b là các số thực bất kì. Trong các mệnh đề sau, mệnh đề nào sai?

A. a > b ⇔ a - b > 0.            

B. a > b> 0 =>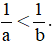            

C. a > b ⇔ a³ > b³.                

D. a > b ⇔ a² > b².

Câu 3. Điều kiện của bất phương trình 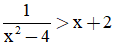 là:

A. x ≠ ±2.                            

B. x ≠ 2.                               

C. x > 2.                               

D. x > 0.

Câu 4. Cho a là số thực dương. Mệnh đề nào dưới đây đúng?

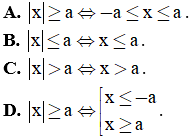
Câu 5. Xét tam giác ABC tùy ý, đường tròn ngoại tiếp tam giác có bán kính R, BC = a. Mệnh đề nào dưới đây đúng ?

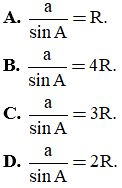
Câu 6. Mệnh đề nào sau đây sai?

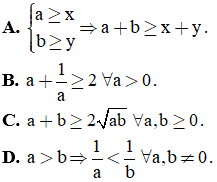
Câu 7. Bất phương trình nào sau đây là bậc nhất một ẩn?

A. 3x > 1 -2x.                      

B.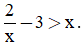                  

C. 2x + y < 1.                        

D. 2x - 1 = 0.

Câu 8. Tập nghiệm của hệ bất phương trình là:

A. [-1; 2]             

B. (-1; 2)             

C. (-1; 2]             

D. [-1; 2)

Câu 9. Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. 2x - 5y + 3z ≤ 0.              

B. 3x² + 2x - 4 > 0.               

C. 2x² + 5y > 3.                    

D. 2x + 3y < 5.

Câu 10. Bất phương trình ax + b > 0 có tập nghiệm là R khi và chỉ khi

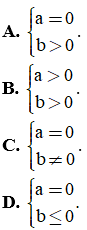
Câu 11. Tam thức nào dưới đây luôn dương với mọi giá trị của x?

A. x² - 10x + 2.                    

B. x² - 2x - 10.                    

C. x² - 2x + 10.                    

D. -x² + 2x + 10.

Câu 12. Cho tam giác ABC có AB = 9, AC = 12, BC = 15. Khi đó đường trung tuyến AM của tam giác có độ dài bằng bao nhiêu?

A. 9.     

B. 10.    

C. 7,5  

D. 8.

Câu 13. Điều kiện xác định của bất phương trình 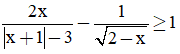 là

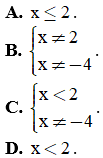
Câu 14. Trong mặt phẳng điểm nào dưới đây thuộc miền nghiệm của hệ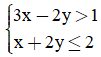

A. P(-1; 0)        

B. N(1; 1)             

C. M(1; -1)                   

D. Q(0; 1)

Câu 15. Bất phương trình 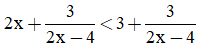 tương đương với:

                       

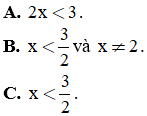
D. Tất cả đều đúng.

Câu 16. Cho tam thức bậc hai có bảng xét dấu như sau

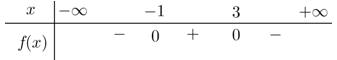
Mệnh đề nào dưới đây đúng ?

A. f(x) ≥ 0 ⇔ -1 ≤ x ≤ 3                                     

B. f(x) ≥ 0 ⇔ x < 3

C. f(x) ≥ 0 ⇔ x > 3                                            

D. f(x) ≥ 0 ⇔ x < -1

Câu 17. Trong mặt phẳng Oxy, cho đường thẳng d: 3x - 2y + 5 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của d

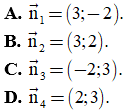
Câu 18. Nhị thức bậc nhất nào dưới đây có bảng xét dấu như sau

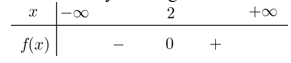
A. f(x) = 2x - 4  

B. f(x) = -x + 3   

C. f(x) = -2x + 4          

D. f(x) = x + 2  

Câu 19. Cho f(x) = ax² + bx + c, (a ≠ 0) và Δ = b² - 4ac. Cho biết dấu của Δ khi f(x) luôn cùng dấu với hệ số a với mọi x ∈ R.

A. Δ < 0.                              

B. Δ = 0.                              

C. Δ > 0.                              

D. Δ ≥ 0.

Câu 20. Xét tam giác ABC tùy ý có BC = a, AC = b, AB = c. Mệnh đề nào dưới đây đúng?

A. a² = b² + c² + 2bc.cosA                                  

B. a² = b² + c² - 2bc.cosA

C. a² = b² + c² - bc.cosA                           

D. a² = b² + c² + bc.cosA

Câu 21. Trong các mệnh đề sau, mệnh đề nào sai?

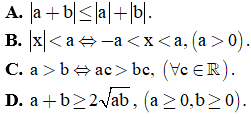
Câu 22. Cho tam giác ABC có a = 2; b = √6; c = 1 + √3. Góc ∠A là 

A. 30⁰.                                  

B. 45⁰.                                  

C. 68⁰.                                  

D. 75⁰. 

Câu 23. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + y ≥ 2?

A. A(-1;2)             

B. B(-2;1)             

C. C(0;1)              

D. D(1;2)

Câu 24. Xét tam giác ABC tùy ý có BC = a, AC = b, AB = c. Diện tích của tam giác ABC bằng

Câu 25. Trong mặt phẳng Oxy, cho hai đường thẳng d₁: x + y + 2 = 0 và d₂: 2x - 3 = 0. Góc giữa hai đường thẳng d₁ và d₂ bằng

A. 60⁰                 

B. 50⁰                 

C. 45⁰                 

D. 90⁰

Câu 26. Trong mặt phẳng Oxy cho đường thẳng 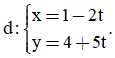 Vectơ nào dưới đây là một vectơ chỉ phương của d

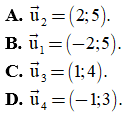
Câu 27. Tập nghiệm của bất phương trình 2x - 1 > 0 là:

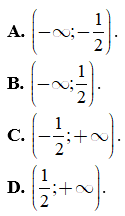
Câu 28. Trong mặt phẳng Oxy xét hai đường thẳng tùy ý d₁: a₁x + b₁y + c₁ = 0 và d₂: a₂x + b₂y + c₂ = 0. Đường thẳng d₁ vuông góc với đường thẳng d₂ khi và chỉ khi

A. a₁a₂ - b₁b₂ = 0

B. a₁b₂ - a₂b₁ = 0

C. a₁b₂ + a₂b₁ = 0

D. a₁a₂ + b₁b₂ = 0

Câu 29. Trong mặt phẳng Oxy, đường thẳng nào dưới đây đi qua điểm A(1;1) ?

A. d₁: 2x + y = 0   

B. d_2: x + y - 2 = 0       

C. d₃: 2x - 3 = 0  

D. d₄: y +1 = 0

Câu 30. Tập nghiệm của bất phương trình 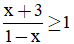 là

A. [-1; 1).                              

B. (-1; 1).                              

C. [-3; 1).                              

D. [-2; 1).

Câu 31. Tập nghiệm của bất phương trình: x² + 9 > 6x là

A. (3; +∞).                  

B. R\{3}.                     

C. R.                  

D. (-∞; 3).

Câu 32. Số nghiệm nguyên của bất phương trình 2x² - 3x - 15 ≤ 0 là

A. 6.     

B. 5.     

C. 8.     

D. 7.

Câu 33. Hai đường thẳng d₁: x - 2y + 1 = 0 và d₂: 2x - 4y + 5 = 0

A. Cắt nhau                    

B. Vuông góc                 

C. Trùng nhau                  

D. Song song

Câu 34. Trong mặt phẳng Oxy, cho điểm M(1; 1) và đường thẳng d: 3x + 4y + 2 = 0. Khoảng cách từ M đến d bằng

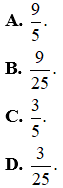
Câu 35. Cho hàm số y = f(x) = ax² + bx + c có đồ thị như hình vẽ. Đặt Δ = b² - 4ac, tìm dấu của a và Δ.

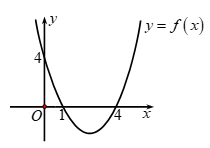
A. a > 0, Δ > 0.                    

B. a < 0, Δ > 0.  

C. a > 0, Δ = 0.                    

D. a < 0, Δ = 0.

II. TỰ LUẬN (4 câu – 3 điểm)

Câu 1(1 điểm). Giải bất phương trình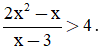 

Câu 2. (1,0 điểm) Cho tam giác ABC có ∠A =  60⁰; AB = 6, AC = 9. Tính diện tích S và đường cao AH của tam giác ABC

Câu 3(0,5 điểm). Tìm m để (m + 1)x² + mx + m < 0, ∀x ∈ R.

Câu 4(0,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình thang cân ABCD có hai đường chéo vuông góc với nhau và cạnh đáy AD = 3BC. Đường thẳng BD có phương trình x + 2y - 6 = 0 và tam giác ABD có trực tâm là H(-3; 2). Tìm tọa độ đỉnh C.

.............................

.............................

.............................

.............................

.............................

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---