Sách bài tập Toán 8 Bài 5: Diện tích hình thoi

Sách bài tập Toán 8 Bài 5: Diện tích hình thoi

Bài 42 trang 162 SBT Toán 8 Tập 1: Trong những hình thoi có chu vi bằng nhau, hãy tìm hình thoi có diện tích lớn nhất.

Lời giải:

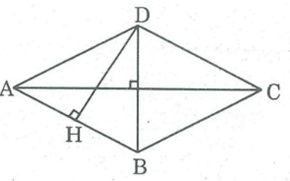
Giả sử có hình thoi ABCD. Kẻ DH ⊥ AB.

Ta có: S_ABCD = AB.DH

Tam giác AHD vuông tại H nên: DH ≤ AD

Mà AB = AD (gt)

Nên: S_ABCD ≤ AB²

Vậy S_ABCD có giá trị lớn nhất bằng AB²

Khi đó ABCD là hình vuông.

Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.

Bài 43 trang 163 SBT Toán 8 Tập 1: Tính diện tích hình thoi, biết cạnh của nó dài 6,2cm và một trong các góc của nó bằng 30°.

Lời giải:

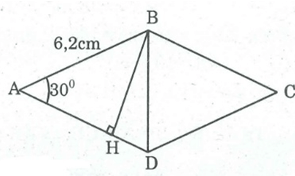
Giả sử hình thoi ABCD có AB = 6,2cm; ∠A = 30^o

Từ B kẻ BH ⊥ AD (H ∈ AD)

Tam giác vuông AHB là một nửa tam giác đều cạnh AB nên:

BH = 1/2 AB = 3,1 (cm)

Vậy S_ABCD = BH.AD = 3,1.6,2 = 19,22 (cm²)

Bài 44 trang 163 SBT Toán 8 Tập 1: Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi.

Lời giải:

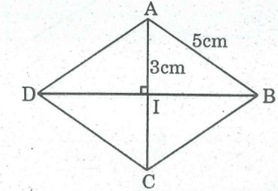
Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: AB² = AI² + IB²

⇒ IB² = AB² - AI² = 25 – 9 = 16

⇒ IB = 4(cm).

AC = 2AI = 2.3 = 6 (cm)

BD = 2IB = 2.4 = 8 (cm)

S_ABCD = 1/2 AC.BD = 1/2 .6.8 = 24 (cm²)

Bài 45 trang 163 SBT Toán 8 Tập 1: a. Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là a và 1/2 a . Hỏi vẽ được bao nhiêu hình như vậy.

b. Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là a và 1/2 a.

c. Hãy tính điện tích các hình vẽ đó

Lời giải:

a. Vẽ được vô số hình tứ giác thỏa mãn yêu cầu

b. Vẽ được duy nhât một hình thm có 2 đường chéo là a và 1/2 a

c. Diện tích các hình vẽ đó là: S = 1/2 a. 1/2 a = 1/4 a² (đvdt).

Bài 46 trang 163 SBT Toán 8 Tập 1: Hai đường chéo hình thoi có độ dài là 16 cm và 12 cm. Tính:

a. Diện tích hình thoi

b. Độ dài cạnh hình thoi

Lời giải:

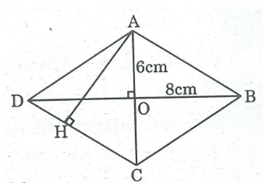
a. Ta có: S_ABCD = 1/2 AC.BD = 1/2 .12.16 = 96 (cm²)

b. ABCD là hình thoi có O là giao điểm của hai đường chéo nên:

AO = OC = 6cm; OB = OD = 8cm

Trong tam giác vuông OAB, ta có:

AB² = OA² + OB² = 6² + 8² = 100

AB = 10 (cm)

c. Kẻ AH ⊥ CD (H ∈ CD)

Ta có: S_ABCD = AH.CD ⇒ AH = S_ABCD / CD = 96/10 = 9,6 (cm)

Bài 5.1 trang 163 SBT Toán 8 Tập 1: a. Sử dụng kéo cắt đúng 2 lần, theo đường thẳng, chia một hình chữ nhật thành ba phần sao cho có thể ghép lại thành một hình thoi.

b. Sử dụng kéo cắt đúng hai lần, theo đường thẳng, chia một hình thoi thành ba phần sao cho có thể ghép lại thành một hình chữ nhật.

Từ đó suy ra công thức tính diện tích hình thoi dựa vào công thức tính diện tích hình chữ nhật.

Lời giải:

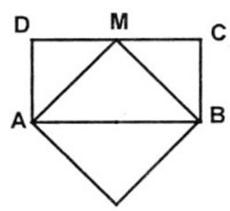
a. Vì hình thoi có hai đường chéo vuông góc cắt nhau tại trung điểm mỗi đường nên chia hình thoi thành 4 tam giác bằng nhau.

Giả sử hình chữ nhật ABCD ta chọn trung điểm M của CD. Nối AM, BM ta cắt theo đường AM và BM ta ghép lại được một hình thoi.

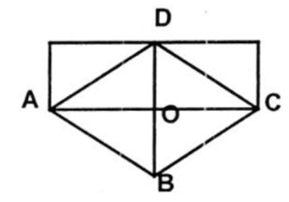
b. Giả sử ta có hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Ta cắt hình thoi theo đường chéo AC ta được 2 tam giác.

Lấy AC làm một cạnh hình chữ nhật. Cắt tam giác BAC theo đường BO ta được hai tam giác ghép lại ta có hình chữ nhật.

Bài 5.2 trang 163 SBT Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM.

a. Chứng minh rằng MNPQ là hình chữ nhật.

b. Tính diện tích của tứ giác XYZT.

Lời giải:

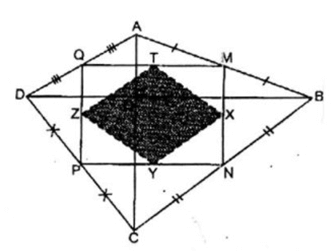
a. Trong ΔABD ta có:

M là trung điểm của AB

Q là trung điểm của AD nên MQ là đường trung bình của ΔABD.

⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)

Trong ΔCBD ta có:

N là trung điểm của BC

P là trung điểm của CD

nên NP là đường trung bình của ΔCBD

⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành

AC ⊥ BD (gt)

MQ // BD

Suy ra: AC ⊥ MQ

Trong ΔABC có MN là đường trung bình ⇒ MN // AC

Suy ra: MN ⊥ MQ hay (NMQ) = 90^o

Vậy tứ giác MNPQ là hình chữ nhật.

b. Kẻ đường chéo MP và NQ

Trong ΔMNP ta có:

X là trung điểm của MN

Y là trung điểm của NP

nên XY là đường trung bình của ΔMNP

⇒ XY // MP và XY = 1/2 MP (tính chất đường trung bình của tam giác) (3)

Trong ΔQMP ta có:

T là trung điểm của QM

Z là trung điểm của QP

nên TZ là đường trung bình của ΔQMP

⇒ TZ // MP và TZ = 1/2 MP (tính chất đường trung bình của tam giác) (4)

Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.

Trong ΔMNQ ta có XT là đường trung bình

⇒ XT = 1/2 QN (tính chất đường trung bình của tam giác)

Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ

Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi

S_XYZT = 1/2 XZ. TY

mà XZ = MQ = 1/2 BD = 1/2. 8 = 4 (cm);

TY = MN = 1/2 AC = 1/2 .6 =3 (cm)

Vậy : S_XYZT = 1/2. 3. 4 = 6( cm²)

Bài 3 trang 163 SBT Toán 8 Tập 1: Cho tam giác vuông ABC, có hai cạnh góc vuông là AC = 6cm và AB = 8cm. Trên cạnh AC lấy điểm D sao cho CD = 5cm. Trên cạnh AB lấy điểm E sao cho EB = 5cm. Gọi M, N, P, Q tương ứng là trung điểm của các đoạn thẳng DE, DB, BC và CE. Tính diện tích của tứ giác MNPQ.

Lời giải:

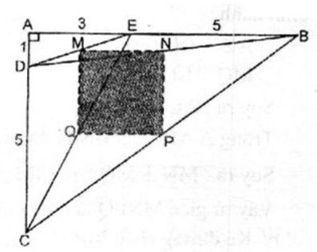
Trong ΔEDC ta có:

M là trung điểm của ED

Q là trung điểm của EC

nên MQ là đường trung bình của ΔEDC

⇒ MQ = 1/2 CD = 2,5 (cm) và MQ // CD

Trong ΔBDC ta có:

N là trung điểm của BD

P là trung điểm của BC

nên NP là đường trung bình của ΔBDC

⇒ NP = 1/2 CD = 2,5 (cm)

Trong ΔDEB ta có:

M là trung điểm của DE

N là trung điểm của DB

nên MN là đường trung bình của ΔDEB

⇒ MN = 1/2 BE = 2,5 (cm) và MN // BE

Trong ΔCEB ta có:

Q là trung điểm của CE

P là trung điểm của CB

nên QP là đường trung bình của ΔCEB

⇒ QP = 1/2 BE = 2,5 (cm)

Suy ra: MN = NP = PQ = QM (1)

MQ // CD hay MQ // AC

AC ⊥ AB (gt)

⇒ MQ ⊥ AB

MN // BE hay MN // AB

Suy ra: MQ ⊥ MN hay (QMN) = 90^o (2)

Từ (1) và (2) suy ra tứ giác MNPQ là hình vuông

S_MNPQ = MN² = (2,5)² = 6,25(cm²)

Xem thêm các bài giải sách bài tập Toán lớp 8 chọn lọc, chi tiết khác:

• Bài 6: Diện tích đa giác
• Ôn tập chương 2 - Phần Hình học
• Bài 1: Mở đầu về phương trình
• Bài 2: Phương trình bậc nhất một ẩn và cách giải

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

• Giải bài tập sgk Toán 8
• Lý thuyết & 700 Bài tập Toán 8 (có đáp án)
• Top 75 Đề thi Toán 8 có đáp án

---