Tóm tắt Lý thuyết Toán lớp 5 Chương 3: Hình học hay, chi tiết

Tài liệu tổng hợp Lý thuyết Toán lớp 5 Chương 3: Hình học hay, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm từ đó học tốt môn Toán lớp 5.

Lý thuyết Toán lớp 5 Chương 3: Hình học

• Lý thuyết Hình tam giác. Diện tích hình tam giác

• Lý thuyết Hình thang. Diện tích hình thang

• Lý thuyết Hình tròn. Đường tròn. Chu vi hình tròn

• Lý thuyết Diện tích hình tròn

• Lý thuyết Hình hộp chữ nhật. Hình lập phương

• Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

• Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình lập phương

• Lý thuyết Thể tích của một hình Xăng-ti-mét khối, Đề-xi-mét khối, Mét khối

• Lý thuyết Thể tích hình hộp chữ nhật

• Lý thuyết Thể tích hình lập phương

---

---

---

Lý thuyết Toán lớp 5 Hình tam giác. Diện tích hình tam giác

1. Hình tam giác

a) Cấu trúc

b) Các loại hình tam giác

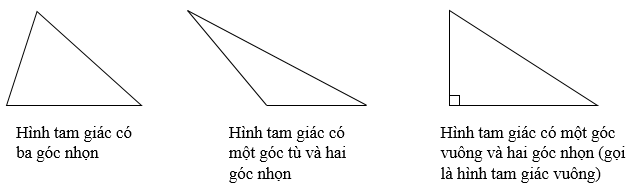
c) Cách xác định đáy và đường cao của hình tam giác

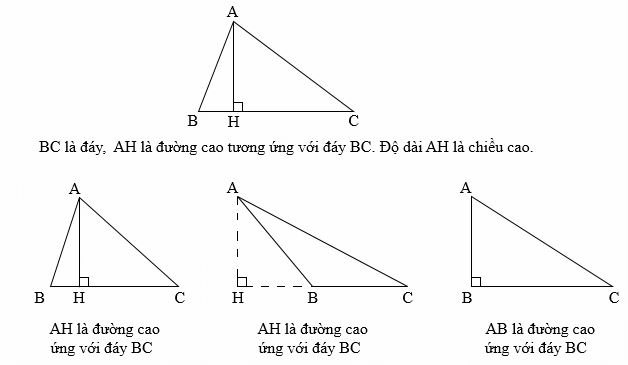
Chú ý: Trong hình tam giác, độ dài đoạn thẳng từ đỉnh vuông góc với đáy tương ứng gọi là chiều cao của hình tam giác

2. Diện tích hình tam giác

Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2

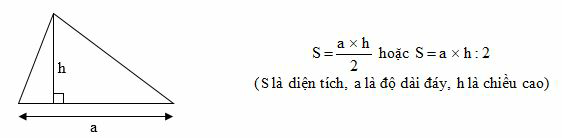
Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho 2.

Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là 13cm và chiều cao là 8cm.

Phương pháp giải: Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2.

Cách giải:

Diện tích hình tam giác đó là:

            13 x 8 : 2 = 52 (cm²)                       

Đáp số: 52cm²

Ví dụ 2: Tính diện tích hình tam giác có độ dài đáy là 2m và chiều cao là 15dm.

Phương pháp giải: Độ dài đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, 2m = 20dm, sau đó tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2

Bài giải

Đổi: 2m = 20dm

Diện tích hình tam giác đó là:

20 x 15 : 2 = 150 dm²

Đáp số: 150 dm²

3) Một số dạng bài tập

Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao

Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao

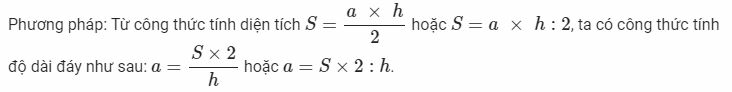
Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy

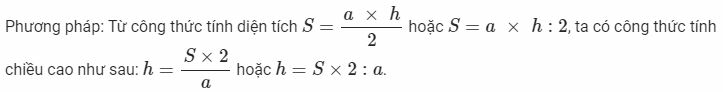
Dạng 4: Toán có lời văn

Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.

Lý thuyết Toán lớp 5 Hình thang. Diện tích hình thang

1. Hình thang

a) Định nghĩa

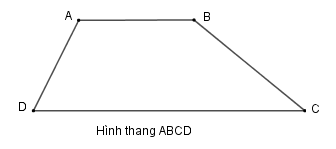
Hình thang ABCD có:

- Cạnh đáy AB và cạnh đáy DC. Cạnh bên AD và cạnh bên BC.

- Hai cạnh đáy là hai cạnh đối diện song song.

Hình thang có một cặp cạnh đối diện song song.

Chú ý: Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.

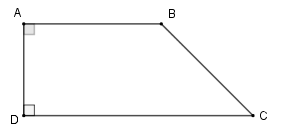
b) Đường cao của hình thang

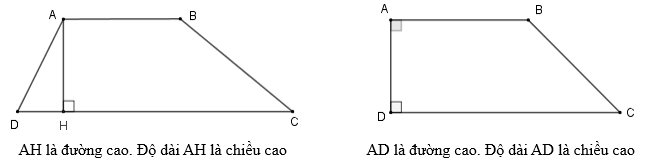
2. Diện tích hình thang

Quy tắc: Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

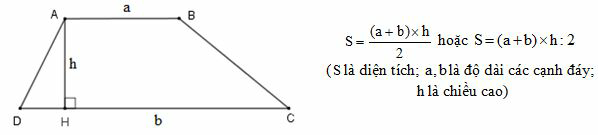
Ví dụ 1: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 18cm và 14cm; chiều cao là 9cm.

Phương pháp giải: Độ dài hai đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.

Bài giải

Diện tích hình thang đó là:

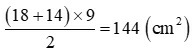
Đáp số: 144cm²

Ví dụ 2: Tính diện tích hình thang biết độ dài hai đáy lần lượt là 4m và 25dm; chiều cao là 32dm.

Phương pháp giải: Độ dài hai đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đó, 4m = 40dm, sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho 2.

Bài giải

Đổi: 4m = 40dm

Diện tích hình thang đó là:

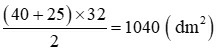
Đáp số: 1040dm²

3. Một số dạng bài tập

Dạng 1: Tính diện tích hình thang khi biết độ dài hai đáy và chiều cao

Phương pháp: 

Áp dụng công thức:   hoặc S = (a + b) × h : 2

(S là diện tích, a, b là độ dài các cạnh đáy, h là chiều cao)

Dạng 2: Tính tổng độ dài hai đáy khi biết diện tích và chiều cao

Phương pháp: Từ công thức tính diện tích 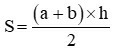  hoặc S = (a + b) × h : 2 ta có công thức tính độ dài hai đáy như sau: a + b = S × 2 : h

Lưu ý: Đề bài thường cho hiệu của hai đáy hoặc tỉ số giữa hai đáy và yêu cầu tìm độ dài của mỗi đáy. Học sinh cần nhớ hai dạng toán tổng – hiệu và tổng – tỉ.

Dạng 3: Tính chiều cao khi biết diện tích và độ dài hai đáy

Phương pháp: Từ công thức tính diện tích 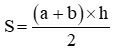  hoặc S = (a + b) × h : 2, ta có công thức tính chiều cao như sau  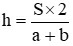 hoặc h = S × 2 : (a + b)

Dạng 4: Toán có lời văn

Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.

Lý thuyết Toán lớp 5 Hình tròn. Đường tròn. Chu vi hình tròn

1. Hình tròn

*) Hình tròn là gì?

Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó.

*) Bán kính

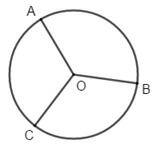
- Nối tâm O với một điểm A trên đường tròn. Đoạn thẳng OA là bán kính của hình tròn.

- Tất cả các bán kính của hình tròn đều bằng nhau: 

OA = OB = OC

- Bán kính đường tròn được kí hiệu là r.

*) Đường kính

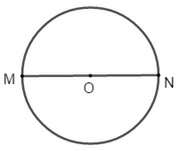
- Đoạn thẳng MN nối hai điểm M, N của đường tròn và đi qua tâm O là đường kính của hình tròn.

- Trong một hình tròn đường kính dài gấp hai lần bán kính. Đường kính được kí hiệu là d.

Đường kính MN gấp 2 lần bán kính ON, OM.

2. Chu vi hình tròn

Quy tắc: Muốn tính chu vi của hình tròn ta lấy đường kính nhân với số 3,14

                                 C = d x 3,14

(C là chu vi hình tròn, d là đường kính hình tròn).

Hoặc: Muốn tính chu vi của hình tròn ta lấy 2 lần bán kính nhân với số 3,14

                                 C = r x 2 x 3,14

(C là chu vi hình tròn, r là bán kính hình tròn).

3. Các dạng bài tập

Dạng 1: Tính chu vi khi biết đường kính

Phương pháp: Áp dụng công thức: C = d x 3,14

(C là chu vi hình tròn, d là đường kính hình tròn).

Ví dụ. Tính chu vi hình tròn có đường kính là 8cm.

Bài giải

Chu vi hình tròn là:

8 x 3,14 = 25,12 (cm)

Đáp số: 25,12cm

Dạng 2: Tính chu vi khi biết bán kính

Phương pháp: Áp dụng công thức: C = r x 2 x 3,14

(C là chu vi hình tròn, r là bán kính hình tròn)

Ví dụ. Tính chu vi hình tròn có bán kính là 3cm.

Bài giải

Chu vi hình tròn là:

3 x 2 x 3,14 = 18,84 (cm)

Đáp số: 18,84cm

Dạng 3: Tính đường kính khi biết chu vi

Phương pháp: Từ công thức tính chu vi C = d x 3,14, ta có thể tính đường kính theo công thức:

d = C : 3,14

Dạng 4: Tính bán kính khi biết chu vi

Phương pháp: Từ công thức tính chu vi C = r x 2 x 3,14, ta có thể tính bán kính theo công thức:

r = C : 3,14 : 2 hoặc r = C : 2 : 3,14.

Ví dụ. Tính bán kính hình tròn khi biết chu vi của hình tròn bằng 12.56 cm.

Bài giải

Bán kính của hình tròn là:

12,56 : 3,14 : 2 = 2 (cm)

Đáp số: 2cm

Dạng 5: Toán có lời văn

Phương pháp: Đọc kĩ đề bài, xác định dạng toán và yêu cầu của đề bài rồi giải bài toán đó.

Ví dụ. Vân đi một vòng xung quanh một cái hồ hình tròn và đếm được 942 bước. Mỗi bước chân của Vân dài 4dm. Tính bán kính của hồ, biết rằng Vân đi sát mép hồ.

Bài giải

Độ dài quãng đường mà Vân đã đi là:

4 × 942 = 3768 (dm)

Chu vi của cái hồ đó là: 3768dm

Đường kính của cái hồ đó là:

3768 : 3,14 = 1200 (dm)

Đổi: 1200dm = 120m

Đáp số: 120m

Xem thêm lý thuyết Toán lớp 5 hay, chi tiết khác:

• Chương 4: Số đo thời gian. Toán chuyển động đều

Xem thêm các bài Để học tốt Toán lớp 5 hay khác:

• Giải Vở bài tập Toán lớp 5
• Giải bài tập Cùng em học Toán lớp 5
• Top 80 Đề thi Toán lớp 5 có đáp án

---