Giải SBT Toán 10 trang 31 Tập 1 Cánh diều

Với Giải sách bài tập Toán 10 trang 31 Tập 1 trong Bài 2: Hệ bất phương trình bậc nhất hai ẩn SBT Toán 10 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 31.

Giải SBT Toán 10 trang 31 Tập 1 Cánh diều

Bài 18 trang 31 SBT Toán 10 tập 1: Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.

Lời giải:

Gọi x (triệu đồng) là số tiền anh Trung đầu tư vào khoản X và y (triệu đồng) là số tiền anh Trung đầu tư vào khoản Y (x, y ≥ 0).

Vì anh Trung đầu tư 400 triệu đồng vào hai khoản X và Y nên ta có x + y ≤ 400.

Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có x ≥ 100 và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta cũng có y ≥ x hay x – y ≤ 0.

Từ đó ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x + y \le 400\\ x \ge 100\\ x - y \le 0\end{array}\right.$

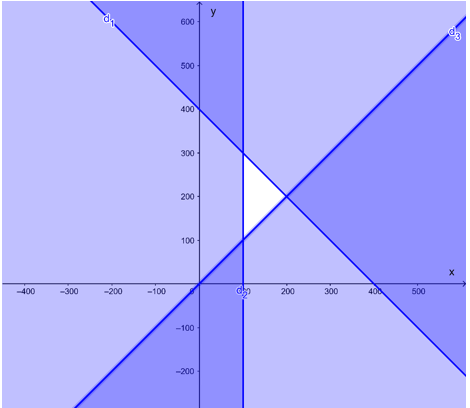
Ta vẽ bốn đường thẳng:

d₁: x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400; 0) và (0; 400);

d₂: x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100; 0);

d₃: x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0; 0) và (1; 1).

Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.

Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với  như hình vẽ sau:

Bài 19 trang 31 SBT Toán 10 tập 1: Một phân xưởng may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết may 1 áo vest hết 2m vải và cần 20 giờ; 1 quần âu hết 1,5 m vải và cần 5 giờ. Xí nghiệp được giao sử dụng không quá 900 m vải và số giờ công không vượt quá 6 000 giờ. Theo khảo sát thị trường, số lượng quần bán ra không nhỏ hơn số lượng áo và không vượt quá 2 lần số lượng áo. Khi xuất ra thị trường, 1 chiếc áo lãi 350 nghìn đồng, 1 chiếc quần lãi 100 nghìn đồng. Phân xưởng cần may bao nhiêu áo vest và quần âu để thu được tiền lãi cao nhất (biết thị trường tiêu thụ luôn đón nhận sản phẩm của xí nghiệp).

Lời giải:

Gọi số lượng áo bán ra là x (cái) (x ∈ ℕ)

Số lượng quần bán ra là y (cái) (y ∈ ℕ).

Số mét vải để may x áo và y quần là: 2x + 1,5y (m).

Vì xí nghiệp được giao sử dụng không quá 900 m vải nên ta có: 2x + 1,5y ≤ 900 (1).

Số giờ để may x áo và y quần là: 20x + 5y (giờ).

Vì số giờ công không vượt quá 6 000 giờ nên ta có: 20x + 5y ≤ 6000 hay 4x + y ≤ 1200 (2).

Theo khảo sát thị trường, ta có:

Số lượng quần bán ra không nhỏ hơn số lượng áo y ≥ x (4)

Số lượng quần không vượt quá 2 lần số lượng áo y ≤ 2x (5)

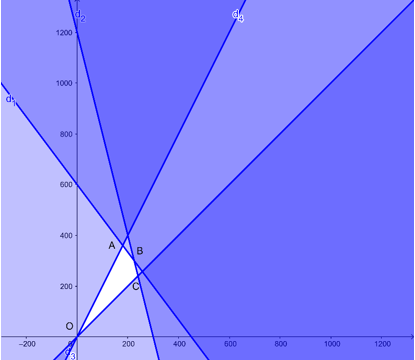
Từ (1), (2), (3) và (4) nên ta có hệ bất phương trình:

$\left\{\begin{array}{l}2x+1,5y \le 900\\ 4x + y \le 1200\\ y \ge x\\ y \le 2x\\ x \ge 0\\ y \ge 0\end{array}\right.\iff \left\{\begin{array}{l}2x+1,5y \le 900\\ 4x + y \le 1200\\ x - y \le 0\\ 2x - y \ge 0\\ x \ge 0\\ y \ge 0\end{array}\right.$

Biểu diễn miền nghiệm của hệ bất phương trình là tứ giác OABC với O(0; 0), A(180; 360), B(200; 250), C(240; 240).

Tiền lãi khi bán x cái áo và y cái quần là 350x + 100y (nghìn đồng).

Đặt T = 350x + 100y.

Ta có biểu thức T = 350x + 100y có giá trị lớn nhất tại một trong các đỉnh của tứ giác OABC.

Tính giá trị biểu thức T tại các đỉnh của tứ giác:

Tại O(0; 0), với x = 0  và y = 0  thì T = 350.0 + 100.0 = 0;

Tại A(180; 360), với x = 180 và y = 360 thì T = 350.180 + 100.360 = 99 000;

Tại B(225; 300), với x = 225 và y = 300 thì T = 350.225 + 100.300 = 108 750;

Tại C(240; 240), với x = 240 và y = 240 thì T = 350.240 + 100.240 = 108 000;

Ta được T đạt giá trị lớn nhất bằng 108 750 000 đồng khi x = 225, y = 300.

Vậy để thu được tiền lãi là cao nhất thì phân xưởng cần may 225 cái áo vest, 300 cái quần âu.

Bài 20 trang 31 SBT Toán 10 Tập 1: Cặp số nào sau đây không là nghiệm của bất phương trình x – 2y ≥ 5?

A. (3; – 1);

B. (– 1; 4);

C. (2; – 3);

D. (1; – 2).

Lời giải:

Đáp án đúng là B

+) Thay x = 3, y = – 1 vào bất phương trình x – 2y ≥ 5, ta được:

3 – 2.(– 1) ≥ 5 ⇔ 5 ≥ 5 (luôn đúng)

Do đó cặp số (3; – 1) là nghiệm của bất phương trình đã cho.

+) Thay x = – 1, y = 4 vào bất phương trình x – 2y ≥ 5, ta được:

3.(– 1) – 2.4 ≥ 5 ⇔ – 11 ≥ 5 (vô lí)

Do đó cặp số (– 1; 4) không là nghiệm của bất phương trình đã cho.

+) Thay x = 2, y = – 3 vào bất phương trình x – 2y ≥ 5, ta được:

3.2 – 2.(– 3) ≥ 5 ⇔ 15 ≥ 5 (luôn đúng)

Do đó cặp số (2; – 3) là nghiệm của bất phương trình đã cho.

+) Thay x = 1, y = – 2 vào bất phương trình x – 2y ≥ 5, ta được:

3.1 – 2.(– 2) ≥ 5 ⇔ 7 ≥ 5 (luôn đúng)

Do đó cặp số (1; – 2) là nghiệm của bất phương trình đã cho.

Bài 21 trang 31 SBT Toán 10 Tập 1: Cặp số nào sau đây không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-2y>4\\ 2x+y>6\end{array}\right.$.

A. (2; – 1);

B. (7; 1);

C. (5; – 1);

D. (6; – 2).

Lời giải:

Đáp án đúng là A

Ta xét hệ bất phương trình: $\left\{\begin{array}{l}x-2y>4\left(1\right)\\ 2x+y>6\left(2\right)\end{array}\right.$

+) Thay x = 2 và y = – 1 vào từng bất phương trình của hệ ta được:

(1) ⇔ 2 – 2(– 1) > 4 ⇔ 4 > 4 (vô lí);

(2) ⇔ 2.2 + (– 1) > 6 ⇔ 3 > 6 (vô lí).

Do đó cặp số (2; – 1) không là nghiệm của hệ bất phương trình đã cho.

+) Thay x = 7 và y = 1 vào từng bất phương trình của hệ ta được:

(1) ⇔ 7 – 2.1 > 4 ⇔ 5 > 4 (luôn đúng);

(2) ⇔ 2.7 + 1 > 6 ⇔ 15 > 6 (luôn đúng).

Do đó cặp số (7; 1) là nghiệm của hệ bất phương trình đã cho.

+) Thay x = 5 và y = – 1 vào từng bất phương trình của hệ ta được:

(1) ⇔ 5 – 2(– 1) > 4 ⇔ 7 > 4 (luôn đúng);

(2) ⇔ 2.5 + (– 1) > 6 ⇔ 9 > 6 (luôn đúng).

Do đó cặp số (5; – 1) là nghiệm của hệ bất phương trình đã cho.

+) Thay x = 6 và y = – 2 vào từng bất phương trình của hệ ta được:

(1) ⇔ 6 – 2(– 2) > 4 ⇔ 10 > 4 (luôn đúng);

(2) ⇔ 2.6 + (– 2) > 6 ⇔ 10 > 6 (luôn đúng).

Do đó cặp số (6; – 2) là nghiệm của hệ bất phương trình đã cho.

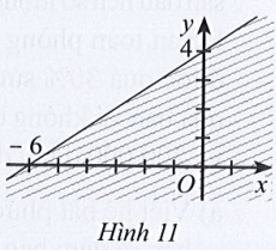
Bài 22 trang 31 SBT Toán 10 Tập 1: Phần không bị gạch (kể cả d) ở Hình 11 là miền nghiệm của bất phương trình:

A. 2x – 3y ≤ – 12;

B. 2x – 3y ≥ – 12;

C. 3x – 2y ≤ 12;

D. 3x – 2y ≥ 12.

Lời giải:

Đáp án đúng là A

Gọi đường thẳng d có dạng: y = ax + b (a

Đường thẳng này cắt hai trục Ox và Oy lần lượt tại các điểm có tọa độ ( – 6; 0) và (0; 4) nên ta có phương trình là: $\frac{x}{-6}+\frac{y}{4}=1\iff$ 2x - 3y = -12.

Lấy điểm O(0; 0) có 2.0 – 3.0 = 0 > – 12, mà điểm O không thuộc miền nghiệm của hệ bất phương trình đã cho và miền nghiệm kể cả d do đó bất phương trình cần tìm là 2x – 3y ≤ – 12.

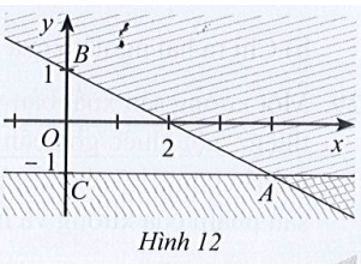
Bài 23 trang 31 SBT Toán 10 Tập 1: Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền nghiệm của hệ bất phương trình:

A. $\left\{\begin{array}{l}x+2y\ge 2\\ y\ge -1·\end{array}\right.$

B. $\left\{\begin{array}{l}x+2y\le 2\\ y\ge -1·\end{array}\right.$

C. $\left\{\begin{array}{l}x+2y<2\\ y>-1·\end{array}\right.$

D. $\left\{\begin{array}{l}x+2y>2\\ y>-1·\end{array}\right.$

Lời giải:

Đáp án đúng là B

Gọi d là đường thẳng đi qua hai điểm A và B, vì đường thẳng này cắt hai trục tọa độ Ox, Oy lần lượt tại các điểm có tọa độ là (2; 0) và (0; 1) nên có phương trình là: $\frac{x}{2}+\frac{y}{1}=1\Rightarrow x+2y=2$

Lấy O(0; 0) có 0 + 2.0 = 0 < 2 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình x + 2y ≤ 2 (1).

Gọi d’ là đường thẳng đi qua hai điểm A và C và song song với trục hoành Ox nên có phương trình y = – 1.

Lấy điểm O(0; 0) có 0 > – 1 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình y ≥ – 1 (2).

Từ (1) và (2) ta có hệ bất phương trình $\left\{\begin{array}{l}x+2y\le 2\\ y\ge -1\end{array}\right.$

Lời giải Sách bài tập Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn Cánh diều hay khác:

• Giải SBT Toán 10 trang 29 Tập 1

• Giải SBT Toán 10 trang 30 Tập 1

• Giải SBT Toán 10 trang 32 Tập 1

• Giải SBT Toán 10 trang 33 Tập 1

Xem thêm lời giải Sách bài tập Toán 10 Cánh diều hay, chi tiết khác:

• SBT Toán 10 Bài tập cuối chương 2 trang 31,32,33

• SBT Toán 10 Bài 1: Hàm số và đồ thị

• SBT Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

• SBT Toán 10 Bài 3: Dấu của tam thức bậc hai

• SBT Toán 10 Bài 4: Bất phương trình bậc hai một ẩn

Xem thêm các tài liệu học tốt lớp 10 hay khác:

• Giải sgk Toán 10 Cánh diều
• Giải Chuyên đề học tập Toán 10 Cánh diều
• Giải SBT Toán 10 Cánh diều
• Giải lớp 10 Cánh diều (các môn học)
• Giải lớp 10 Kết nối tri thức (các môn học)
• Giải lớp 10 Chân trời sáng tạo (các môn học)

---