Giải SBT Toán 10 trang 39 Tập 1 Kết nối tri thức

Với Giải SBT Toán 10 trang 39 Tập 1 trong Bài 6: Hệ thức lượng trong tam giác Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 39.

Giải SBT Toán 10 trang 39 Tập 1 Kết nối tri thức

Bài 3.9 trang 39 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có a = 4, $\hat{C}=60°,$ b = 5.

a) Tính các góc và cạnh còn lại của tam giác.

b) Tính diện tích của tam giác.

c) Tính độ dài đường trung tuyến kẻ từ đỉnh A của tam giác.

Lời giải:

Áp dụng định lí côsin cho DABC ta có:

c² = a² + b² – 2ab.cosC

Þ c² = 4² + 5² – 2.4.5.cos60°

= 16 + 25 – 40.$\frac{1}{2}$ = 21.

$\Rightarrow$c = $\sqrt{21}.$

Áp dụng định lí sin ta có: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

Do đó:

$\sin B=\frac{\sin C}{c}.b=\frac{\sin 60°}{\sqrt{21}}.5=\frac{5\sqrt{7}}{14}.$

$\Rightarrow \hat{B}\approx 70°{53}^{\text{'}}3{6^{\text{'}}}^{\text{'}}$

$\sin A=\frac{\sin C}{c}.a=\frac{\sin 60°}{\sqrt{21}}.4=\frac{2\sqrt{7}}{7}.$

$\Rightarrow \hat{A}\approx 49°6^{\text{'}}2{4^{\text{'}}}^{\text{'}}$

Vậy $c=\sqrt{21};\hat{A}\approx 49°6^{\text{'}}2{4^{\text{'}}}^{\text{'}};\hat{B}\approx 70°{53}^{\text{'}}3{6^{\text{'}}}^{\text{'}}.$

b) Áp dụng công thức tính diện tích tam giác ta có:

$S=\frac{1}{2}.ab\sin C=\frac{1}{2}\mathrm{.4.5.}\sin 60°=5\sqrt{3}.$

Vậy diện tích tam giác ABC bằng $5\sqrt{3}.$

c) Áp dụng công thức tính độ dài đường trung tuyến trong phần Nhận xét của Ví dụ 3, trang 37, Sách bài tập, Toán 10, Tập một ta có:

$m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}=\frac{5^2+{\left(\sqrt{21}\right)}^2}{2}-\frac{4^2}{4}=19.$

$\Rightarrow m_a=\sqrt{19}.$

Vậy độ dài đường trung tuyến kẻ từ đỉnh A của tam giác ABC bằng $\sqrt{19}.$

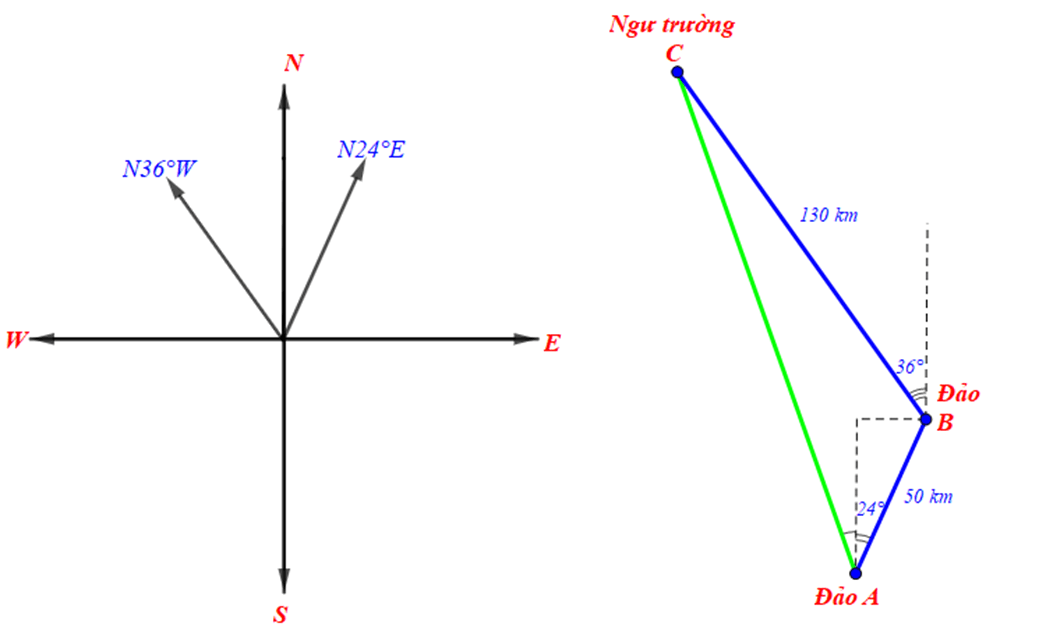
Bài 3.10 trang 39 sách bài tập Toán lớp 10 Tập 1: Một tàu cá xuất phát từ đảo A, chạy 50 km theo hướng N24°E đến đảo B để lấy thêm ngư cụ, rồi chuyển hướng N36°W chạy tiếp 130 km đến ngư trường C.

a) Tính khoảng cách từ vị trí xuất phát A đến C (làm tròn đến hàng đơn theo đơn vị đo kilômét).

b) Tìm hướng từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị độ).

Lời giải:

Ba vị trí đảo A, đảo B và ngư trường C được mô tả như hình vẽ đưới đây:

a) Ta có: $\widehat{ABC}=\left(90°-24°\right)+\left(90°-36°\right)=120°$

Áp dụng định lí côsin cho tam giác ABC ta có:

AC² = AB² + BC² – 2.AB.BC.cos$\widehat{ABC}$

= 50² + 130² – 2.50.130.$\left(-\frac{1}{2}\right)$ = 25 900

$\Rightarrow AC=10\sqrt{259}\approx 161\left(km\right)$

Vậy khoảng cách từ đảo A đến ngư trường C khoảng 161 km.

b) Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{BC}{\sin \widehat{BAC}}=\frac{AC}{\sin \widehat{ABC}}$

$\Rightarrow \sin \widehat{BAC}=\frac{\sin \widehat{ABC}}{AC}.BC$

$\Rightarrow \sin \widehat{BAC}\approx \frac{\sin 120°}{161}.130\approx 0,699$

$\Rightarrow \widehat{BAC}\approx 44°.$

Do đó AC có hướng chếch về hướng W một góc 44° – 24° = 22° so với hướng N.

Vậy từ A đến C có hướng N20°W.

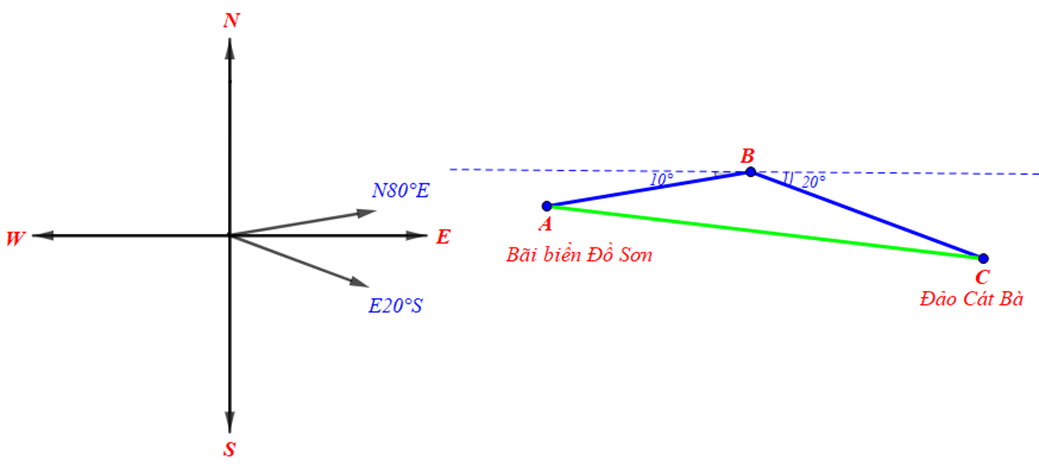
Bài 3.11 trang 39 sách bài tập Toán lớp 10 Tập 1: Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng N80°E với vận tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng E20°S giữ nguyên vận tốc và chạy tiếp 36 phút nữa đến đảo Cát Bà. Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômet?

Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng N80°E với vận tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng E20°S giữ nguyên vận tốc và chạy tiếp 36 phút nữa đến đảo Cát Bà. Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômet?

Lời giải:

Giả sử tàu du lịch xuất phát từ điểm A, chuyển động theo hướng N80°E tới B sau đó chuyển hướng E20°S tới điểm C như hình vẽ dưới đây.

Ta có: $\widehat{ABC}=180°-10°-20°=150°$

Tàu chạy từ A đến B với vận tốc 20 km/h trong 30 phút (= 0,5 giờ) nên:

AB = 20.0,5 = 10 (km).

Tàu chạy từ B đến C với vận tốc 20 km/h trong 36 phút (= 0,6 giờ) nên:

BC = 20.0,6 = 12 (km)

Áp dụng định lí côsin cho tam giác ABC ta được:

AC² = AB² + BC² – 2.AB.BC.cos$\widehat{ABC}$

= 10² + 12² – 2.10.12.cos150°

= 100 + 144 – 240.$\left(-\frac{\sqrt{3}}{2}\right)$ = 452 (km)

Suy ra $AC\approx \sqrt{452}\approx 21,26\left(km\right).$

Vậy khi tới đảo Cát Bà thì tàu du lịch cách vị trí xuất phát (bãi biển Đồ Sơn) khoảng 21,26 km.

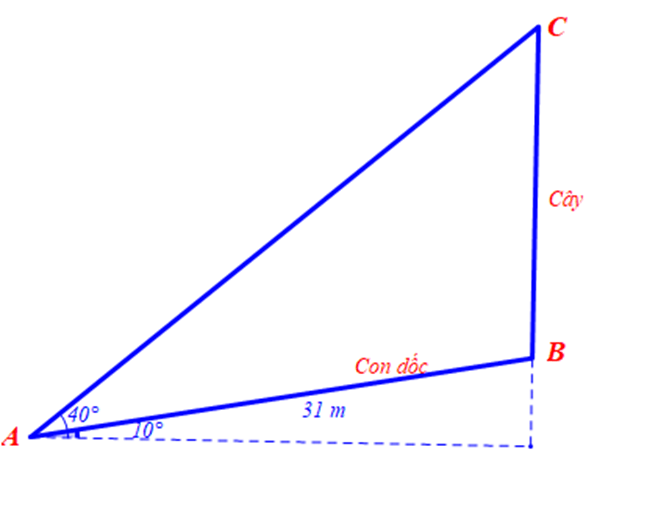
Bài 3.12 trang 39 sách bài tập Toán lớp 10 Tập 1: Một cây cổ thụ mọc thẳng đứng bên lề một con dốc có độ dốc 10 độ so với phương nằm ngang. Từ một điểm dưới chân dốc, cách gốc cây 31 m người ta nhìn đỉnh ngọn cây dưới một góc 40° so với phương nằm ngang. Hãy tính chiều cao của cây.

Lời giải:

Cây cổ thụ và con dốc được mô tả như hình vẽ dưới đây:

Vì con dốc có độ dốc 10° so với phương nằm ngang, người nhìn nhìn đỉnh ngọn cây dưới một góc 40° so với phương nằm ngang nên ta có $\widehat{BAC}=40°-10°=30°.$

Và $\widehat{ACB}=90°-40°=50°$

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{AB}{\sin \widehat{ACB}}=\frac{BC}{\sin \widehat{BAC}}$

$\Rightarrow BC=\frac{AB}{\sin \widehat{ACB}}.\sin \widehat{BAC}$

$\Rightarrow BC=\frac{31}{\sin 50°}.\sin 30°\approx 20,23\left(m\right)$

Vậy chiều cao của cây khoảng 20,23 m.

Bài 3.13 trang 39 sách bài tập Toán lớp 10 Tập 1:

Cho tam giác ABC. Chứng minh rằng:

a) $\cot A+\cot B+\cot C=\frac{a^2+b^2+c^2}{4S};$

b) $m_a^2+m_b^2+m_c^2=\frac{3}{4}\left(a^2+b^2+c^2\right).$

Lời giải:

a) Áp dụng định lí côsin ta có:

cosA = $\frac{b^2+c^2-a^2}{2bc}$ (1)

Áp dụng công thức tính diện tích tam giác ta có:

$S=\frac{1}{2}bc.\sin A$

$\Rightarrow \sin A=\frac{2S}{bc}$ (2)

Từ (1) và (2) ta có:

cotA = $\frac{\cos A}{\sin A}=\frac{b^2+c^2-a^2}{2bc}:\frac{2S}{bc}$

$\Rightarrow \cot A=\frac{b^2+c^2-a^2}{2bc}.\frac{bc}{2S}$

$\Rightarrow \cot A=\frac{b^2+c^2-a^2}{4S}.$

Chứng minh tương tự ta cũng có:

$\cot B=\frac{a^2+c^2-b^2}{4S}$ và $\cot C=\frac{a^2+b^2-c^2}{4S}$

Do đó cotA + cotB + cotC

$=\frac{b^2+c^2-a^2}{4S}+\frac{a^2+c^2-b^2}{4S}+\frac{a^2+b^2-c^2}{4S}$

$=\frac{a^2+b^2+c^2}{4S}$

Vậy $\cot A+\cot B+\cot C=\frac{a^2+b^2+c^2}{4S}.$

b) Áp dụng công thức tính độ dài đường trung tuyến ta có:

$m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4};$ $m_b^2=\frac{a^2+c^2}{2}-\frac{b^2}{4}$ và $m_c^2=\frac{a^2+b^2}{2}-\frac{c^2}{4}.$

Do đó:

$m_a^2+m_b^2+m_c^2$

$=\frac{b^2+c^2}{2}-\frac{a^2}{4}+\frac{a^2+c^2}{2}-\frac{b^2}{4}+\frac{a^2+b^2}{2}-\frac{c^2}{4}$

$=\frac{2\left(a^2+b^2+c^2\right)}{2}-\frac{a^2+b^2+c^2}{4}$

$=\left(a^2+b^2+c^2\right)-\frac{1}{4}\left(a^2+b^2+c^2\right)$

$=\frac{3}{4}\left(a^2+b^2+c^2\right).$

Vậy $m_a^2+m_b^2+m_c^2=\frac{3}{4}\left(a^2+b^2+c^2\right).$

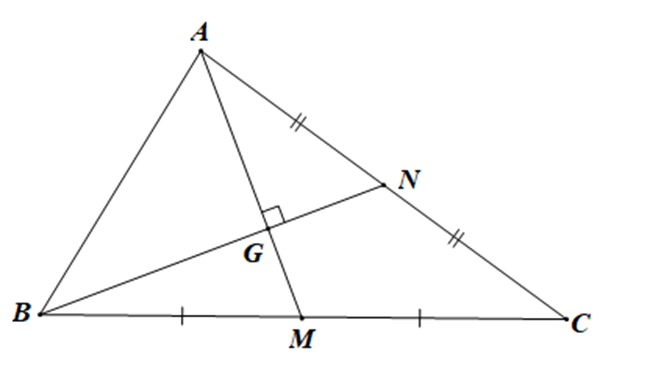
Bài 3.14 trang 39 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có hai trung tuyến kẻ từ A và B vuông góc.

Chứng minh rằng:

a) a² + b² = 5c²;

b) cotC= 2 (cot A + cot B).

Lời giải:

a)

Gọi M, N lần lượt là trung điểm của các cạnh BC, AC.

Gọi G là trọng tâm của tam giác ABC.

Khi đó $AG=\frac{2}{3}AM$ và $BG=\frac{2}{3}BN.$

Áp dụng định lí Pythagore cho tam giác ABG vuông tại G (do AM ⊥ BN) có:

c² = AB² = AG² + BG²

$=\frac{4}{9}.A{M}^2+\frac{4}{9}.B{N}^2$

Mà AM, BN là hai đường trung tuyến kẻ từ A và B của tam giác ABC.

Do đó theo công thức tính độ dài đường trung tuyến của tam giác ta có:

$A{M}^2=m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}$ và $B{N}^2=m_b^2=\frac{a^2+c^2}{2}-\frac{b^2}{4}.$

Suy ra c² = $\frac{4}{9}.\left(\frac{b^2+c^2}{2}-\frac{a^2}{4}\right)+\frac{4}{9}.\left(\frac{a^2+c^2}{2}-\frac{b^2}{4}\right)$

$=\frac{4}{9}.\left(\frac{b^2+c^2}{2}-\frac{a^2}{4}+\frac{a^2+c^2}{2}-\frac{b^2}{4}\right)$

$=\frac{4}{9}.\left(\frac{a^2+b^2}{4}+c^2\right)$

$\Rightarrow$ c² $=\frac{4}{9}.\left(\frac{a^2+b^2}{4}+c^2\right)$

$\Rightarrow$ 9c² = a² + b² + 4c²

$\Rightarrow$ 5c² = a² + b².

b) Theo chứng minh phần a), Bài 3.13 ta có:

$\cot C=\frac{a^2+b^2-c^2}{4S}$

Mà 5c² = a² + b² (chứng minh phần a))

Do đó $\cot C=\frac{5c^2-c^2}{4S}=\frac{4c^2}{4S}=\frac{c^2}{S}$ (1)

Mặt khác:

$\cot A+\cot B=\frac{b^2+c^2-a^2}{4S}+\frac{a^2+c^2-b^2}{4S}$

$\Rightarrow$ cotA + cotB $=\frac{2c^2}{4S}=\frac{c^2}{2S}$

$\Rightarrow$ 2(cotA + cotB) $=\frac{c^2}{S}$ (2)

Từ (1) và (2) ta có: cotC = 2(cotA + cotB) = $\frac{c^2}{S}.$

Vậy cotC = 2(cotA + cotB).

Bài 3.15 trang 39 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có các góc thoả mãn $\frac{\sin A}{1}=\frac{\sin B}{2}=\frac{\sin C}{\sqrt{3}}.$ Tính số đo các góc của tam giác.

Lời giải:

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

$\Rightarrow \sin A=\frac{a}{2R};\sin B=\frac{b}{2R};\sin C=\frac{c}{2R}.$

Theo bài ta có: $\frac{\sin A}{1}=\frac{\sin B}{2}=\frac{\sin C}{\sqrt{3}}.$

$\Rightarrow \frac{\frac{a}{2R}}{1}=\frac{\frac{b}{2R}}{2}=\frac{\frac{c}{2R}}{\sqrt{3}}$$\Rightarrow \frac{a}{1}=\frac{b}{2}=\frac{c}{\sqrt{3}}$

Đặt $\frac{a}{1}=\frac{b}{2}=\frac{c}{\sqrt{3}}=t$

Suy ra a = t; b = 2t; c = t$\sqrt{3}.$

Suy ra a² = t²; b = 4t²; c = 3t².

Ta thấy: a² + c² = b² = 4t²

Theo định lí Pythagore đảo ta có tam giác ABC vuông tại B.

$\Rightarrow$ sinB = 1.

$\Rightarrow \frac{\sin A}{1}=\frac{1}{2}=\frac{\sin C}{\sqrt{3}}.$

$\Rightarrow \sin A=\frac{1}{2}$ và $\sin C=\frac{\sqrt{3}}{2}$

$\Rightarrow$$\hat{A}=30°$ và $\hat{C}=60°.$

Vậy $\hat{A}=30°;\hat{B}=90°$ và $\hat{C}=60°.$

Bài 3.16 trang 39 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có S = 2R².sin A.sinB. Chứng minh rằng tam giác ABC là một tam giác vuông.

Lời giải:

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

$\Rightarrow$ a = 2R.sinA; b = 2R.sinB và c = 2R.sinC.

Theo công thức tính diện tích tam giác ta có:

$S=\frac{abc}{4R}=\frac{\left(2R\sin A\right).\left(2R\sin B\right).\left(2R\sin C\right)}{4R}$

$\Rightarrow S=\frac{8R^3.\sin A.\sin B.\sin C}{4R}$

$\Rightarrow$ S = 2R².sin A.sinB.sinC.

Mà theo bài S = 2R².sin A.sinB.

Do đó sinC = 1

$\Rightarrow \hat{C}=90°.$

Vậy tam giác ABC vuông tại C.

Lời giải Sách bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác Kết nối tri thức hay khác:

• Giải SBT Toán 10 trang 38 Tập 1

Xem thêm lời giải Sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

• SBT Toán 10 Bài tập cuối chương 3 trang 40, 41, 42, 43, 44

• SBT Toán 10 Bài 7: Các khái niệm mở đầu

• SBT Toán 10 Bài 8: Tổng và hiệu của hai vectơ

• SBT Toán 10 Bài 9: Tích của một vectơ với một số

• SBT Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ

Xem thêm các tài liệu học tốt lớp 10 hay khác:

• Giải sgk Toán 10 Kết nối tri thức
• Giải Chuyên đề học tập Toán 10 Kết nối tri thức
• Giải SBT Toán 10 Kết nối tri thức
• Giải lớp 10 Kết nối tri thức (các môn học)
• Giải lớp 10 Chân trời sáng tạo (các môn học)
• Giải lớp 10 Cánh diều (các môn học)

---