Giải SBT Toán 10 trang 18 Tập 2 Kết nối tri thức
Với Giải SBT Toán 10 trang 18 Tập 2 trong Bài 17: Dấu của tam thức bậc hai Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 18.
Giải SBT Toán 10 trang 18 Tập 2 Kết nối tri thức
Bài 6.21 trang 18 Sách bài tập Toán lớp 10 Tập 2: Xét dấu các tam thức bậc hai sau:
a) f(x) = –x2 + 6x + 7;
b) g(x) = 3x2 – 2x + 2;
c) h(x) = –16x2 + 24x – 9;
d) k(x) = 2x2 – 6x + 1.
Hướng dẫn giải:
a)
f(x) = –x2 + 6x + 7 có a = –1 < 0
f(x) = 0 ⇔ –x2 + 6x + 7 = 0
Xét phương trình bậc hai –x2 + 6x + 7 = 0 có ∆ = b2 – 4ac = 62 – 4.(–1).7 = 64 > 0
Do đó, phương trình có hai nghiệm phân biệt:
Vậy f(x) = –x2 + 6x + 7 < 0 với x ∈ (–∞; –1) ∪ (7; +∞), f(x) = –x2 + 6x + 7 > 0 với x ∈ (–1; 7).
b)
g(x) = 3x2 – 2x + 2 có a = 3 > 0
g(x) = 0 ⇔ 3x2 – 2x + 2 = 0
Xét phương trình bậc hai 3x2 – 2x + 2 = 0 có ∆ = b2 – 4ac = (–2)2 – 4.3.2 = –20 < 0.
Vậy g(x) = 3x2 – 2x + 2 > 0 với x ∈ ℝ.
c)
h(x) = –16x2 + 24x – 9 có a = –16 < 0
h(x) = 0 ⇔ –16x2 + 24x – 9 = 0
Xét phương trình bậc hai –16x2 + 24x – 9 = 0 có ∆ = b2 – 4ac = 242 – 4.(–16).(–9) = 0
Vậy phương trình có nghiệm kép: .
Vậy h(x) < 0 với x R \ {} và h(x) = 0 tại .
d)
k(x) = 2x2 – 6x + 1 có a = 2 > 0
k(x) = 0 ⇔ 2x2 – 6x + 1 = 0
Xét phương trình bậc hai 2x2 – 6x + 1 = 0 có ∆ = b2 – 4ac = (–6)2 – 4.2.1 = 28 > 0
Do đó, phương trình có hai nghiệm phân biệt:
Vậy k(x) < 0 với x ∈ và k(x) > 0 với x ∈ .
Bài 6.22 trang 18 Sách bài tập Toán lớp 10 Tập 2: Giải các bất phương trình sau:
a) 3x2 – 36x + 108 > 0;
b) –x2 + 2x – 2 ≥ 0;
c) x4 – 3x2 + 2 ≤ 0;
d) .
Hướng dẫn giải:
a)
Xét tam thức bậc hai f(x) = 3x2 – 36x + 108 có a = 3 > 0
Phương trình bậc hai 3x2 – 36x + 108 = 0 có ∆ = b2 – 4ac = (–36)2 – 4.3.108 = 0
Do đó, phương trình có nghiệm kép x = 6.
Do đó, f(x) = 3x2 – 36x + 108 > 0 với x ∈ ℝ\{6}
Hay tập nghiệm của bất phương trình 3x2 – 36x + 108 > 0 là S = ℝ\{6}.
b)
Xét tam thức bậc hai f(x) = –x2 + 2x – 2 có a = –1 < 0
Phương trình bậc hai –x2 + 2x – 2 = 0 có ∆ = b2 – 4ac = 22 – 4.(–1).(–2) = –4 < 0
Do đó, f(x) = –x2 + 2x – 2 < 0 với mọi x ∈ ℝ
Hay tập nghiệm của bất phương trình –x2 + 2x – 2 ≥ 0 là S = ∅.
c)
x4 – 3x2 + 2 ≤ 0
Đặt t = x2 (t ≥ 0), khi đó, bất phương trình trở thành:
t2 – 3t + 2 ≤ 0
Xét tam thức bậc hai f(t) = t2 – 3t + 2 có a = 1 > 0
Phương trình bậc hai t2 – 3t + 2 = 0 có ∆ = b2 – 4ac = (–3)2 – 4.1.2 = 1 > 0
Do đó, phương trình có hai nghiệm phân biệt là:
Do đó, f(t) = t2 – 3t + 2 < 0 với t ∈ (1; 2) ⇒ t2 – 3t + 2 ≤ 0 với t ∈ [1; 2] (thỏa mãn điều kiện t ≥ 0).
Ta có t ∈ [1; 2] ⇒ 1 ≤ t ≤ 2 ⇒ 1 ≤ x2 ≤ 2
Hay tập nghiệm của bất phương trình x4 – 3x2 + 2 ≤ 0 là S = [;-1][1;].
d)
Xét phương trình bậc hai x2 – x + 1 = 0 có a = 1 > 0 và ∆1 = (–1)2 – 4.1.1 = –3 < 0 do đó, x2 – x + 1 > 0 với mọi số thực x.
Xét phương trình bậc hai 2x2 + x + 2 = 0 có a = 2 > 0 và ∆2 = 12 – 4.2.2 = –15 < 0 do đó, 2x2 + x + 2 > 0 với mọi số thực x
Do đó, tập xác định của bất phương trình là D = ℝ.
Khi đó,
⇔ 2x2 + x + 2 ≤ x2 – x + 1
⇔ x2 + 2x + 1 ≤ 0
⇔ (x + 1)2 ≤ 0
Do (x + 1)2 ≥ 0 với mọi số thực x nên ta có:
(x + 1)2 ≤ 0
⇔ (x + 1)2 = 0
⇔ x + 1 = 0
⇔ x = –1
Vậy tập nghiệm của bất phương trình là S = {–1}.
Bài 6.23 trang 18 Sách bài tập Toán lớp 10 Tập 2: Tìm các giá trị của tham số m để phương trình x2 – 2(m – 1)x + 4m2 – m = 0
a) có hai nghiệm phân biệt;
b) có hai nghiệm trái dấu.
Hướng dẫn giải:
Xét x2 – 2(m – 1)x + 4m2 – m = 0 có:
a = 1 > 0
∆’ = [–(m – 1)]2 – 1.(4m2 – m) = m2 – 2m + 1 – 4m2 + m = –3m2 – m + 1 .
a)
Để phương trình x2 – 2(m – 1)x + 4m2 – m = 0 có hai nghiệm phân biệt
⇔ ∆’ > 0
⇔ –3m2 – m + 1 > 0
Xét phương trình bậc hai –3m2 – m + 1 = 0 có a = –3 < 0 và ∆ma = (–1)2 – 4.(–3).1 = 13 > 0
Do đó, phương trình –3m2 – m + 1 = 0 có hai nghiệm phân biệt là:
Do đó, –3m2 – m + 1 > 0
Vậy khi thì phương trình x2 – 2(m – 1)x + 4m2 – m = 0 có hai nghiệm phân biệt.
b) Để phương trình x2 – 2(m – 1)x + 4m2 – m = 0 có hai nghiệm trái dấu
⇔ ac < 0
⇔ 1.(4m2 – m ) < 0
⇔ 4m2 – m < 0
Xét phương trình bậc hai 4m2 – m = 0 có a = 4 > 0 và ∆mb = (–1)2 – 4.4.0 = 1 > 0
Do đó, phương trình bậc hai 4m2 – m = 0 có hai nghiệm phân biệt là:
Do đó, 4m2 – m < 0 ⇔
Vậy khi thì phương trình x2 – 2(m – 1)x + 4m2 – m = 0 có hai nghiệm trái dấu.
Bài 6.24 trang 18 Sách bài tập Toán lớp 10 Tập 2: Tìm các giá trị của tham số m để
a) –x2 + (m + 1)x – 2m + 1 ≤ 0, ∀x ∈ ℝ;
b) x2 – (2m + 1)x + m + 2 > 0, ∀x ∈ ℝ.
Hướng dẫn giải:
a)
Xét phương trình –x2 + (m + 1)x – 2m + 1 = 0 có:
a = –1 < 0
∆ = (m + 1)2 – 4.(–1).(–2m + 1) = m2 + 2m + 1 – 8m + 4 = m2 – 6m + 5
Để –x2 + (m + 1)x – 2m + 1 ≤ 0, ∀x ∈ ℝ ⇔ Δ ≤ 0
⇔ m2 – 6m + 5 ≤ 0
Xét phương trình m2 – 6m + 5 = 0 có a = 1 > 0 và Δm = (–6)2 – 4.1.5 = 16 > 0
Do đó, phương trình m2 – 6m + 5 = 0 có hai nghiệm phân biệt là:
m1 = 1; m2 = 5
Do đó, m2 – 6m + 5 ≤ 0 ⇔ 1 ≤ m ≤ 5
Vậy khi 1 ≤ m ≤ 5 thì –x2 + (m + 1)x – 2m + 1 ≤ 0, ∀x ∈ ℝ.
b)
x2 – (2m + 1)x + m + 2 > 0, ∀x ∈ ℝ
Xét phương trình x2 – (2m + 1)x + m + 2 = 0 có:
a = 1 > 0
∆ = [–(2m + 1)]2 – 4.1.(m + 2) = 4m2 + 4m + 1 – 4m – 8 = 4m2 – 7
Để x2 – (2m + 1)x + m + 2 > 0, ∀x ∈ ℝ ⇔ Δ < 0
⇔ 4m2 – 7 < 0
⇔
⇔
Vậy khi thì x2 – (2m + 1)x + m + 2 > 0, ∀x ∈ ℝ.
Bài 6.25 trang 18 Sách bài tập Toán lớp 10 Tập 2: Một công ty đồ gia dụng sản xuất bình đựng nước thấy rằng khi đơn giá của bình đựng nước là x nghìn đồng thì doanh thu R (tính theo đơn vị nghìn đồng) sẽ là R(x) = –560x2 + 50 000x.
a) Theo mô hình doanh thu này, thì đơn giá nào là quá cao dẫn đến doanh thu từ việc bán bình đựng nước bằng 0 (tức là sẽ không có người mua)?
b) Với khoảng đơn giá nào của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt mức 1 tỉ đồng ?
Hướng dẫn giải:
a)
Đơn giá của bình đựng nước là x nghìn đồng (x > 0).
Doanh thu từ việc bán bình đựng nước bằng 0 tức là
R(x) = 0
⇔ –560x2 + 50 000x = 0
⇔ x = 0 (loại) hoặc x ≈ 89 (thỏa mãn)
Vậy theo mô hình đã cho, với đơn giá 89 nghìn đồng thì công ty sẽ không có doanh thu (đơn giá cao quá dẫn đến không có ai mua hàng).
b)
Doanh thu vượt mức 1 tỉ đồng tức là
R(x) = –560x2 + 50 000x > 1 000 000
⇔ –560x2 + 50 000x – 1 000 000 > 0
Xét phương trình bậc hai –560x2 + 50 000x – 1 000 000 = 0 có:
a = –560 < 0
Δ’ = 25 0002 – (–560).(– 1 000 000) = 65 000 000 > 0
Do đó, phương trình bậc hai –560x2 + 50000x – 1000000 = 0 có hai nghiệm phân biệt là:
x1 ≈ 59,04; x2 ≈ 30,25.
Do đó, –560x2 + 50 000x – 1 000 000 > 0 ⇔ 30,25 < x < 59,04 hay 31 < x < 59.
Vậy với khoảng đơn giá từ 31 nghìn đồng đến 59 nghìn đồng của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt mức 1 tỉ đồng.
Bài 6.26 trang 18 Sách bài tập Toán lớp 10 Tập 2: Một viên đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu 500 m/s, hợp với phương ngang một góc bằng 45°. Biết rằng khi bỏ qua sức cản của không khí, quỹ đạo chuyển động của một vật ném xiên sẽ tuân theo phương trình:
,
trong đó x là khoảng cách (tính bằng mét) vật bay được theo phương ngang, vận tốc ban đầu v0 của vật hợp với phương ngang một góc α và g = 9,8 m/s2 là gia tốc trọng trường.
a) Viết phương trình chuyển động của viên đạn.
b) Để viên đạn bay qua một ngọn núi cao 4 000 mét thì khẩu pháo phải đặt cách chân núi một khoảng cách bao xa ?
Hướng dẫn giải:
a)
Một viên đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu 500 m/s, hợp với phương ngang một góc bằng 45° nên ta có:
g = 9,8 m/s2 ; v0 = 500 m/s; α = 45°
Phương trình chuyển động của viên đạn là:
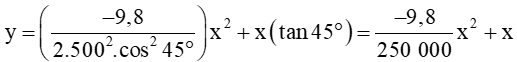
b)
Để viên đạn bay qua một ngọn núi cao 4 000 mét thì
Xét phương trình bậc hai có:
a = < 0
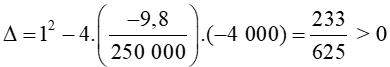
Do đó, phương trình bậc hai có hai nghiệm phân biệt là:
x1 ≈ 20 543; x2 ≈ 4 967
Do đó, ⇔ 4 967 < x < 20 543
Vậy khẩu pháo phải đặt cách chân núi trong khoảng từ 4 967 m đến 20 543 m (tất nhiên là phải tính đến tầm bắn của khẩu pháo nữa) thì viên đạn sẽ bay qua đỉnh núi.
Lời giải sách bài tập Toán 10 Bài 17: Dấu của tam thức bậc hai Kết nối tri thức hay khác:
Xem thêm lời Giải sách bài tập Toán 10 Kết nối tri thức hay, chi tiết khác:
SBT Toán 10 Bài 18: Phương trình quy về phương trình bậc hai
SBT Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách
Xem thêm các tài liệu học tốt lớp 10 hay khác:
- Giải sgk Toán 10 Kết nối tri thức
- Giải Chuyên đề học tập Toán 10 Kết nối tri thức
- Giải SBT Toán 10 Kết nối tri thức
- Giải lớp 10 Kết nối tri thức (các môn học)
- Giải lớp 10 Chân trời sáng tạo (các môn học)
- Giải lớp 10 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 10 (hay nhất) - KNTT
- Soạn văn 10 (ngắn nhất) - KNTT
- Soạn văn 10 (siêu ngắn) - KNTT
- Giải sgk Toán 10 - KNTT
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Giải sgk Vật lí 10 - KNTT
- Giải sgk Hóa học 10 - KNTT
- Giải sgk Sinh học 10 - KNTT
- Giải sgk Địa lí 10 - KNTT
- Giải sgk Lịch sử 10 - KNTT
- Giải sgk Kinh tế và Pháp luật 10 - KNTT
- Giải sgk Tin học 10 - KNTT
- Giải sgk Công nghệ 10 - KNTT
- Giải sgk Hoạt động trải nghiệm 10 - KNTT
- Giải sgk Giáo dục quốc phòng 10 - KNTT

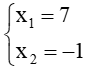
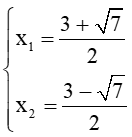
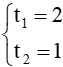
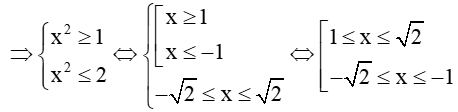



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

