Giải Toán 11 trang 58 Tập 1 Cánh diều
Với Giải Toán 11 trang 58 Tập 1 trong Bài tập cuối chương 2 Toán 11 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 58.
Giải Toán 11 trang 58 Tập 1 Cánh diều
Bài 8 trang 58 Toán 11 Tập 1: Xét tính tăng, giảm và bị chặn của mỗi dãy số (un) sau, biết số hạng tổng quát:
a) ;
b) ;
c) un = (– 1)n.n2.
Lời giải:
a) Ta có:
Xét hiệu
> 0 với mọi n ∈ ℕ*.
Vì vậy dãy số đã cho là dãy số tăng.
b) Ta có:
Xét hiệu < 0
Vì vậy dãy số đã cho là dãy số giảm.
Bài 9 trang 58 Toán 11 Tập 1: Cho cấp số cộng (un). Tìm số hạng đầu u1, công sai d trong mỗi trường hợp sau:
a) u2 + u5 = 42 và u4 + u9 = 66;
b) u2 + u4 = 22 và u1.u5 = 21.
Lời giải:
a) Ta có: u2 + u5 = u1 + d + u1 + 3d = 42
⇔ 2u1 + 4d = 42
Ta lại có: u4 + u9 = u1 + 3d + u1 + 8d = 2u1 + 11d = 66
Khi đó ta có hệ phương trình:
Vậy số hạng đầu của cấp số cộng là: và công sai d=.
b) Ta có: u2 + u4 = u1 + d + u1 + 3d = 22
⇔ 2u1 + 4d = 22
⇔ u1 + 2d = 11
⇔ u1 = 11 – 2d
Ta lại có: u1.u5 = u1(u1 + 4d) = 21.
Thay u1 = 11 – 2d vào biểu thức trên ra được:
(11 – 2d)(11 – 2d + 4d) = 21
⇔ (11 – 2d)(11 + 2d) = 21
⇔ 121 – 4d2 = 21
⇔ d = 5 hoặc d = – 5.
Với d = 5 thì u1 = 1.
Với d = – 5 thì u1 = 21.
Bài 10 trang 58 Toán 11 Tập 1: Cho cấp số nhân (un). Tìm số hạng đầu u1, công bội q trong mỗi trường hợp sau:
a) u6 = 192 và u7 = 384;
b) u1 + u2 + u3 = 7 và u5 – u2 = 14.
Lời giải:
a) Ta có u6 = u1.q5 = 192 và u7 = u1.q6 = 384
Xét:
Suy ra: u1 = 192: = 6144.
Vậy cấp số nhân có số hạng đầu u1 = 6 144 và công bội q=.
b) Ta có: u1 + u2 + u3 = u1 + u1.q + u1.q2 = 7
⇔ u1(1 + q + q2) = 7
Và u5 – u2 = u1.q4 – u1.q = 14
⇔ u1q(q3 – 1) = 14
Suy ra:
⇔ 2 = q(q – 1)
⇔ q2 – q – 2 = 0
⇔ q = 2 hoặc q = – 1.
Với q = 2 thì u1 = 1.
Với q = – 1 thì u1 = 7.
Bài 11 trang 58 Toán 11 Tập 1: Tứ giác ABCD có số đo bốn góc A, B, C, D theo thứ tự lập thành cấp số cộng. Biết số đo góc C gấp 5 lần số đo góc A. Tính số đo các góc của tứ giác ABCD theo đơn vị độ.
Lời giải:
Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:
B = A + d; C = A + 2d; D = A + 3d.
Mặt khác: A + B + C + D = 360°
⇔ A + A + d + A + 2d + A + 3d = 360°
⇔ 4A + 6d = 360°
⇔ 2A + 3d = 180°
Ta lại có: A + 2d = 5A ⇔ d = 2A
⇒ 8A = 180°
⇒ A = 22,5° và d = 45°
⇒ B = 67,5°, C = 112,5°, D = 157,5°.
Bài 12 trang 58 Toán 11 Tập 1: Người ta trồng cây theo các hàng ngang với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ở hàng thứ 3 có 3 cây, ... ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4 950 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
Lời giải:
Giải sữ người ta đã trồng được n hàng.
Số cây ở mỗi hàng lập thành một cấp số cộng với u1 = 1, công sai d = 1
Tổng số cây ở n hàng cây là:
= 4950
⇔ n2 + n – 9 900 = 0
⇔ n = 99 (thỏa mãn) hoặc n = – 100 (không thỏa mãn)
Vậy có 99 hàng cây được trồng theo cách trên.
Bài 13 trang 58 Toán 11 Tập 1: Một cái tháp có 11 tầng. Diện tích của mặt sàn tầng 2 bằng nửa diện tích của mặt đáy tháp và diện tích của mặt sàn mỗi tầng bằng nửa diện tích của mặt sàn mỗi tầng ngay bên dưới. Biết mặt đáy tháp có diện tích là 12 288 m2. Tính diện tích của mặt trên cùng của tháp theo đơn vị mét vuông.
Lời giải:
Diện tích mặt đáy tháp là u1 = 12 288 (m2).
Diện tích mặt sàn tầng 2 là: u2 = 12 288. = 6 144 (m2).
...
Gọi diện tích mặt sàn tầng n là un với n ∈ ℕ*.
Dãy (un) lập thành một cấp số nhân là u1 = 12 288 và công bội q=, có số hạng tổng quát là: un = 12 288..
Diện tích mặt tháp trên cùng chính là mặt tháp thứ 11 nên ta có:
u11 = 12 288. = 12 (m2).
Bài 14 trang 58 Toán 11 Tập 1: Một khay nước có nhiệt độ 23°C được đặt vào ngăn đá tủ lạnh. Biết sau mỗi giờ, nhiệt độ của nước giảm 20%. Tính nhiệt độ của khay nước đó sau 6 giờ theo đơn vị độ C.
Lời giải:
Gọi un là nhiệt độ của khay nước đó sau n giờ (đơn vị độ C) với n ∈ ℕ*.
Ta có: u1 = 23; u2 = 23 – 23.20% = 23.(1 – 20%) = 23.80%; u3 = 23.80%.80% = 23.(80%)2; ...
Suy ra dãy (un) lập thành một cấp số nhân với số hạng đầu u1 = 23 và công bội q = 80% có số hạng tổng quát un = 23.(80%)n – 1 độ C.
Vậy sau 6 giờ thì nhiệt độ của khay là u6 = 23.(80%)5 ≈ 7,5°C.
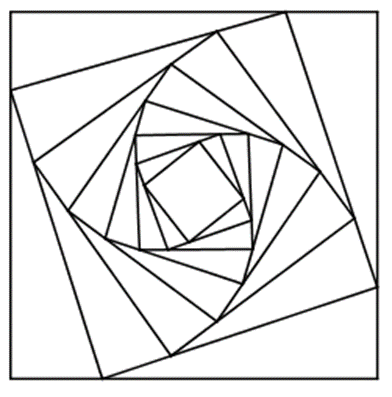
Bài 15 trang 58 Toán 11 Tập 1: Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (Hình 4). Từ hình vuông C2 lại làm tiếp tục như trên để có hình vuông C3. Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông C1, C2, C3, ..., Cn, ... Gọi an là độ dài cạnh hình vuông Cn. Chứng minh dãy số (an) là cấp số nhân.
Lời giải:
Độ dài cạnh của hình vuông đầu tiên là: a1 = 4.
Độ dài cạnh của hình vuông thứ n là: an.
Độ dài cạnh của hình vuông thứ n + 1 là: an+1 = .
Suy ra:
Vậy (an) là một cấp số nhân với số hạng đầu a1 = 4 và công bội q = .
Bài 16 trang 58 Toán 11 Tập 1: Ông An vay ngân hàng 1 tỉ đồng với lãi suất 12%/năm. Ông đã trả nợ theo cách: Bắt đầu từ tháng thứ nhất sau khi vay, cuối mỗi tháng ông trả ngân hàng cùng số tiền là a (đồng) và đã trả hết nợ sau đúng 2 năm kể từ ngày vay. Hỏi số tiền mỗi tháng mà ông An phải trả là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?
Lời giải:
Gọi un là số tiền sau mỗi tháng ông An còn nợ ngân hàng.
Lãi suất mỗi tháng là 1%.
Ta có:
u1 = 1 000 000 000 đồng.
u2 = u1 + u1.1% - a = u1(1 + 1%) – a (đồng)
u3 = u1(1 + 1%) – a + [u1(1 + 1%) – a].1% – a = u1(1 + 1%)2 – a(1 + 1%) – a
...
un = u1(1 + 1%)n-1 – a(1 + 1%)n-2 – a(1 + 1%)n-3 – a(1 + 1%)n-4 – ... – a.
Ta thấy dãy a(1 + 1%)n-2; a(1 + 1%)n-3; a(1 + 1%)n-4; ...; a lập thành một cấp số nhân với số hạng đầu a1 = a và công bội q = 1 + 1% = 99% có tổng n – 2 số hạng đầu là:
100a[1 – (99%)n-2].
Suy ra un = u1(1 + 1%)n-1 – 100a[1 – (99%)n-2].
Vì sau 2 năm = 24 tháng thì ông An trả xong số tiền nên n = 24 và u24 = 0. Do đó ta có:
u24 = u1(1 + 1%)23 – 100a[1 – (99%)22] = 0
⇔ 1 000 000 000.(99%)23 – 100a[1 – (99%)22] = 0
⇔ a = 40 006 888,25
Vậy mỗi tháng ông An phải trả 40 006 888,25 đồng.
Lời giải bài tập Toán 11 Bài tập cuối chương 2 hay khác:
Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 11 hay khác:
- Giải sgk Toán 11 Cánh diều
- Giải Chuyên đề học tập Toán 11 Cánh diều
- Giải SBT Toán 11 Cánh diều
- Giải lớp 11 Cánh diều (các môn học)
- Giải lớp 11 Kết nối tri thức (các môn học)
- Giải lớp 11 Chân trời sáng tạo (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 11 Cánh diều (hay nhất)
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Toán 11 - Cánh diều
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Giải sgk Vật Lí 11 - Cánh diều
- Giải sgk Hóa học 11 - Cánh diều
- Giải sgk Sinh học 11 - Cánh diều
- Giải sgk Lịch Sử 11 - Cánh diều
- Giải sgk Địa Lí 11 - Cánh diều
- Giải sgk Giáo dục KTPL 11 - Cánh diều
- Giải sgk Tin học 11 - Cánh diều
- Giải sgk Công nghệ 11 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 - Cánh diều
- Giải sgk Giáo dục quốc phòng 11 - Cánh diều
- Giải sgk Âm nhạc 11 - Cánh diều

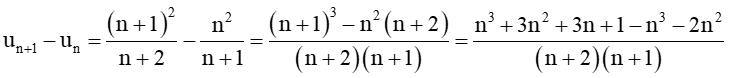





 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

