Giải Toán 12 trang 97 Tập 2 Cánh diều

Với Giải Toán 12 trang 97 Tập 2 trong Bài 2: Công thức xác suất toàn phần. Công thức Bayes Toán 12 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 97.

Giải Toán 12 trang 97 Tập 2 Cánh diều

Câu hỏi khởi động trang 97 Toán 12 Tập 2: Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ngẫu nhiên ra một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.

Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Lời giải:

Sau bài học này, ta giải quyết được bài toán trên như sau:

Xét hai biến cố sau:

A: “Linh kiện được chọn ra đạt tiêu chuẩn”;

B: “Linh kiện được chọn ra do nhà máy I sản xuất”.

Khi đó, ta có:

P(B) = 0,55; P( $\overline{B}$) = 1 – P(B) = 1 – 0,55 = 0,45;

P(A | B) = 0,9; P(A | $\overline{B}$ ) = 0,87.

Áp dụng công thức xác suất toàn phần, ta có:

P(A) = P(B) ∙ P(A | B) + P($\overline{B}$ ) ∙ P(A | $\overline{B}$ ) = 0,55 ∙ 0,9 + 0,45 ∙ 0,87 = 0,8865.

Vậy xác suất để linh kiện được lấy ra đạt tiêu chuẩn bằng 0,8865.

Hoạt động 1 trang 97 Toán 12 Tập 2: Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biết cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.

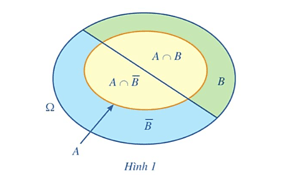
a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, A ∩ B, $A\cap \overline{B}$ (Hình 1).

 

Từ đó, hãy chứng tỏ rằng: P(A) = P(A ∩ B) + P($A\cap \overline{B}$ ).

c) So sánh: P(A ∩ B) và P(B) ∙ P(A | B);

                  P( $A\cap \overline{B}$) và P($\overline{B}$ ) ∙ P(A | $\overline{B}$ ).

Từ đó, hãy chứng tỏ rằng: P(A) = P(B) ∙ P(A | B) + P( $\overline{B}$) ∙ P(A | $\overline{B}$ ).

Lời giải:

a) Ω = {1; 2; 3; …; 24}.

A = {3; 6; 9; 12; 15; 18; 21; 24}.

B = {4; 8; 12; 16; 20; 24}.

A ∩ B = {12; 24}.

$\overline{B}$ = {1; 2; 3; 5; 6; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19; 21; 22; 23}.

A ∩ $\overline{B}$  = {3; 6; 9; 15; 18; 21}.

b) Từ câu a), suy ra n(A) = 8, n(A ∩ B) = 2, n(A ∩ $\overline{B}$ ) = 6.

Do 8 = 2 + 6 nên n(A) = n(A ∩ B) + n( $A\cap \overline{B}$).

Khi đó, P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$  = $\frac{n\left(A\cap B\right)+n\left(A\cap \overline{B}\right)}{n\left(\Omega \right)}$  = $\frac{n\left(A\cap B\right)}{n\left(\Omega \right)}$  + $\frac{n\left(A\cap \overline{B}\right)}{n\left(\Omega \right)}$ .

Mà P(A ∩ B) = $\frac{n\left(A\cap B\right)}{n\left(\Omega \right)}$ ; P($A\cap \overline{B}$ ) = $\frac{n\left(A\cap \overline{B}\right)}{n\left(\Omega \right)}$ .

Vậy P(A) = P(A ∩ B) + P( $A\cap \overline{B}$).

c) Ta có P(B) ∙ P(A | B) = P(B) ∙ $\frac{P\left(A\cap B\right)}{P\left(B\right)}$  = P(A ∩ B).

P( $\overline{B}$) ∙ P(A | $\overline{B}$ ) = P( $\overline{B}$) ∙ $\frac{P\left(A\cap \overline{B}\right)}{P\left(\overline{B}\right)}$  = P( $A\cap \overline{B}$).

Vì hai biến cố A ∩ B và $A\cap \overline{B}$  là hai biến cố xung khắc và (A ∩ B) ∪ ($A\cap \overline{B}$ ) = A nên theo công thức xác suất ta có

P(A) = P(A ∩ B) + P($A\cap \overline{B}$ ) = P(B) ∙ P(A | B) + P( $\overline{B}$) ∙ P(A | $\overline{B}$ ).

Lời giải bài tập Toán 12 Bài 2: Công thức xác suất toàn phần. Công thức Bayes hay khác:

• Giải Toán 12 trang 100
• Giải Toán 12 trang 101
• Giải Toán 12 trang 102

Xem thêm lời giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

• Toán 12 Bài 2: Phương trình đường thẳng

• Toán 12 Bài 3: Phương trình mặt cầu

• Toán 12 Bài tập cuối chương 5

• Toán 12 Bài 1: Xác xuất có điều kiện

• Toán 12 Bài tập cuối chương 6

Xem thêm các tài liệu học tốt lớp 12 hay khác:

• Giải sgk Toán 12 Cánh diều
• Giải Chuyên đề học tập Toán 12 Cánh diều
• Giải SBT Toán 12 Cánh diều
• Giải lớp 12 Cánh diều (các môn học)
• Giải lớp 12 Kết nối tri thức (các môn học)
• Giải lớp 12 Chân trời sáng tạo (các môn học)

---