HĐ10 trang 38 Toán 12 Tập 2 - Kết nối tri thức

Giải Toán 12 Bài 14: Phương trình mặt phẳng - Kết nối tri thức

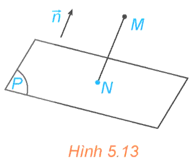
HĐ10 trang 38 Toán 12 Tập 2: Trong không gian Oxyz, cho điểm M(x0; y0; z0) và mặt phẳng (P): Ax + By + Cz + D = 0 có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$. Gọi N là hình chiếu vuông góc của M trên (P) (H.5.13).

a) Giải thích vì sao tồn tại số k để $\overrightarrow{MN}=k\overrightarrow{n}$. Tính tọa độ của N theo k, tọa độ của M và các hệ số A, B, C, D.

b) Thay tọa độ của N vào phương trình mặt phẳng (P) để từ đó tính k theo tọa độ của M và các hệ số A, B, C, D.

c) Từ $\left|\overrightarrow{MN}\right|=\left|k\right|\left|\overrightarrow{n}\right|$, hãy tính độ dài của đoạn thẳng MN theo tọa độ của M và các hệ số A, B, C, D. Từ đó suy ra công thức tính khoảng cách từ điểm M đến mặt phẳng (P).

Lời giải:

a) Vì N là hình chiếu vuông góc của M trên (P) nên $MN\perp \left(P\right)$

Do đó $\overrightarrow{MN}$ sẽ cùng phương với vectơ pháp tuyến $\overrightarrow{n}$

Vậy tồn tại một số k sao cho $\overrightarrow{MN}=k\overrightarrow{n}$

Giả sử N(x₁; y₁; z₁). Suy ra $\overrightarrow{MN}=\left(x_1-x_0;y_1-y_0;z_1-z_0\right)$

Vì $\overrightarrow{MN}=k\overrightarrow{n}$ nên $\left\{\begin{array}{l}{x}_1-x_0=kA\\ y_1-y_0=kB\\ z_1-z_0=kC\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_1=x_0+kA\\ y_1=y_0+kB\\ z_1=z_0+kC\end{array}\right.$

b) Thay tọa độ điểm N vào (P), ta được

A(x₀ + kA) + B(y₀ + kB) + C(z₀ + kC) + D = 0

⇔ k(A² + B² + C²) + Ax₀ + By₀ + Cz₀ + D = 0

$\iff k=\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}$

c) Ta có $\left|\overrightarrow{MN}\right|=\left|k\right|\left|\overrightarrow{n}\right|$$\iff \left|\overrightarrow{MN}\right|=\left|k\right|\sqrt{A^2+B^2+C^2}$

Mà $k=\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}$ nên $MN=\left|\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}\right|\sqrt{A^2+B^2+C^2}$

$\iff MN=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$

Do đó khoảng cách từ điểm M đến mặt phẳng (P) là $d=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$

Lời giải bài tập Toán 12 Bài 14: Phương trình mặt phẳng hay, chi tiết khác:

• Mở đầu trang 29 Toán 12 Tập 2: Một vật thể chuyển động trong không gian Oxyz. Tại mỗi thời điểm t, vật thể ở vị trí M(cost – sint; cost + sint; cost) ....

• HĐ1 trang 29 Toán 12 Tập 2: Trên mặt bàn phẳng, đặt một vật. Khi đó, mặt bàn tác động lên vật phản lực pháp tuyến $\overrightarrow{n}$, giá của vectơ $\overrightarrow{n}$ vuông góc với mặt bàn ....

• Luyện tập 1 trang 30 Toán 12 Tập 2: Trong không gian Oxyz, cho các điểm A(1; −2; 3), B(−3; 0; 1). Gọi (α) là mặt phẳng trung trực của đoạn thẳng AB ....

• HĐ2 trang 30 Toán 12 Tập 2: Trong không gian Oxyz, cho hai vectơ $\overrightarrow{u}=\left(a;b;c\right)$ và $\overrightarrow{v}=\left(a^{\text{'}};b^{\text{'}};c^{\text{'}}\right)$. ....

• Luyện tập 2 trang 31 Toán 12 Tập 2: Trong không gian Oxyz, cho $\overrightarrow{u}=\left(2;3;1\right)$ và $\overrightarrow{v}=\left(4;6;2\right)$. Tính $\left[\overrightarrow{u},\overrightarrow{v}\right]$ ....

• HĐ3 trang 31 Toán 12 Tập 2: Trong không gian Oxyz, cho hai vectơ $\overrightarrow{u},\overrightarrow{v}$ không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P) ....

• Luyện tập 3 trang 31 Toán 12 Tập 2: Trong không gian Oxyz, cho ba điểm không thẳng hàng A(1; −2; 1), B(−2; 1; 0), C(−2; 3; 2) ....

• Vận dụng 1 trang 31 Toán 12 Tập 2: Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể ....

• HĐ4 trang 32 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α). Gọi $\overrightarrow{n}=\left(A;B;C\right)$ là một vectơ pháp tuyến của (α) ....

• Luyện tập 4 trang 32 Toán 12 Tập 2: Trong không gian Oxyz, phương trình nào trong các phương trình sau là phương trình tổng quát của một mặt phẳng? ....

• Luyện tập 5 trang 33 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α): x + 2 = 0. ....

• HĐ5 trang 33 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$ ....

• Luyện tập 6 trang 33 Toán 12 Tập 2: Trong không gian Oxyz, viết phương trình mặt phẳng (α) đi qua điểm M(1; 2; −4) và vuông góc với trục Oz ....

• HĐ6 trang 33 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M(x₀; y₀; z₀) và biết cặp vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right)$, $\overrightarrow{v}=\left(a^{\text{'}};b^{\text{'}};c^{\text{'}}\right)$ ....

• Luyện tập 7 trang 34 Toán 12 Tập 2: Trong không gian Oxyz, cho các điểm A(1; −2; −1), B(4; 1; 2), C(2; 3; 1). Viết phương trình mặt phẳng (α) đi qua ....

• HĐ7 trang 34 Toán 12 Tập 2: Trong không gian Oxyz, cho ba điểm không thẳng hàng: A(1; 2; 3), B(−1; 3; 4), C(2; −1; 2) ....

• Luyện tập 8 trang 35 Toán 12 Tập 2: (H.5.8) Trong không gian Oxyz, cho mặt phẳng (α) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm ....

• Vận dụng 2 trang 35 Toán 12 Tập 2: Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra ....

• HĐ8 trang 35 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng: (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'z + D' = 0 ....

• Luyện tập 9 trang 36 Toán 12 Tập 2: Trong không gian Oxyz, hai mặt phẳng sau đây có vuông góc với nhau hay không? (α): 3x + y – z + 1 = 0, (β): 9x + 3y – 3z + 3 = 0 ....

• Vận dụng 3 trang 36 Toán 12 Tập 2: (H.5.10) Trong không gian Oxyz, sàn của một căn phòng có dạng hình tứ giác với bốn đỉnh O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), $C\left(0;2\sqrt{2};0\right)$ ....

• HĐ9 trang 37 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'x + D' = 0, với các vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right),\overrightarrow{n^{\text{'}}}=\left(A^{\text{'}};B^{\text{'}};C^{\text{'}}\right)$ ....

• Luyện tập 10 trang 37 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng: (α): 5x + 2y – 4z + 6 = 0 và (β): 10x + 4y – 2z + 12 = 0 ....

• Vận dụng 4 trang 37 Toán 12 Tập 2: Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh ....

• Luyện tập 11 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y + z + 2 = 0 và (Q): x + 3y + z + 5 = 0 ....

• Vận dụng 5 trang 39 Toán 12 Tập 2: (H.5.14) Góc quan sát ngang của một camera là 115°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) ....

• Bài 5.1 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, viết phương trình mặt phẳng đi qua điểm M(1; 2; −1) và vuông góc với trục Ox ....

• Bài 5.2 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D', với A(1; −1; 3), B(0; 2; 4), D(2; −1; 1), A'(0; 1; 2) ....

• Bài 5.3 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1; −1; 5) và vuông góc với hai mặt phẳng (Q): 3x + 2y – z = 0, (R): x + y – z = 0 ....

• Bài 5.4 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, viết phương trình mặt phẳng đi qua M(2; 3; −1), song song với trục Ox và vuông góc với mặt phẳng (Q): x + 2y – 3z + 1 = 0 ....

• Bài 5.5 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, tính khoảng cách từ gốc tọa độ đến mặt phẳng (P): 2x + 2y – z + 1 = 0 ....

• Bài 5.6 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (P): x + y + z + 2 = 0, (Q): x + y + z + 6 = 0 ....

• Bài 5.7 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y – z = 0, (Q): x – y – 2z + 1 = 0 ....

• Bài 5.8 trang 39 Toán 12 Tập 2: Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều ....

• Bài 5.9 trang 39 Toán 12 Tập 2: Trong không gian Oxyz, một ngôi nhà có sàn nhà thuộc mặt phẳng Oxy, trần nhà tầng 1 thuộc mặt phẳng z – 1 = 0 ....

• Bài 5.10 trang 40 Toán 12 Tập 2: Xét một cối xay lúa trong không gian Oxyz, với đơn vị đo là mét. Nếu tác động vào tai cối xay lúa (ở vị trí P) ....

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

• Toán 12 Bài 15: Phương trình đường thẳng trong không gian

• Toán 12 Bài 16: Công thức tính góc trong không gian

• Toán 12 Bài 17: Phương trình mặt cầu

• Toán 12 Bài tập cuối chương 5

• Toán 12 Bài 18: Xác suất có điều kiện

Xem thêm các tài liệu học tốt lớp 12 hay khác:

• Giải sgk Toán 12 Kết nối tri thức
• Giải Chuyên đề học tập Toán 12 Kết nối tri thức
• Giải SBT Toán 12 Kết nối tri thức
• Giải lớp 12 Kết nối tri thức (các môn học)
• Giải lớp 12 Chân trời sáng tạo (các môn học)
• Giải lớp 12 Cánh diều (các môn học)

---