Hình vuông lớp 3 (Lý thuyết + Các dạng bài tập)
Lý thuyết & Bài tập Hình vuông Toán lớp 3 chương trình sách mới với đầy đủ lý thuyết và phương pháp giải các dạng bài tập giúp bạn nắm vững kiến thức trọng tâm Hình vuông lớp 3.
Hình vuông lớp 3 (Lý thuyết + Các dạng bài tập)
Lý thuyết Hình vuông
Các dạng bài tập Hình vuông
Dạng 1. Nhận diện hình vuông
- Dựa vào các dấu hiệu đã nêu ở phần trên để kiểm tra.
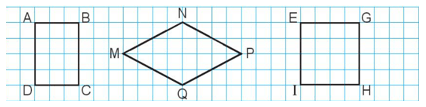
Ví dụ: Kiểm tra trong các hình vẽ sau đây, hình nào là hình vuông? Cho biết các đỉnh, góc, cạnh của hình vuông đó?
Dựa vào các dấu hiệu nêu trên, và sau khi kiểm tra, ta thấy hình EGHI là hình vuông (có 4 đỉnh, 4 góc vuông, 4 cạnh có độ dài bằng nhau)
+ 4 đỉnh: E, G, H, I
+ 4 góc vuông: góc đỉnh E, góc đỉnh G, góc đỉnh H, góc đỉnh I
+ 4 cạnh bằng nhau: EG, GH, HI, IE
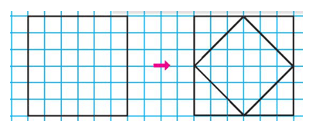
Dạng 2: Vẽ và trang trí hình vuông
- Vẽ 4 đỉnh của hình vuông
- Dùng thước thẳng vẽ các cạnh
- Trang trí hình vuông
Ví dụ:
Dạng 3: Tìm độ dài cạnh của hình vuông
Bốn cạnh của hình vuông có độ dài bằng nhau
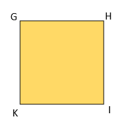
Ví dụ: Cho hình vuông GHIK có độ dài cạnh GK là 3 cm. Tính độ dài các cạnh còn lại của hình vuông?
Lời giải
Do tứ giác GHIK là hình vuông nên độ dài các cạnh bằng nhau.
Khi đó ta có: GK = GH = HI = IK
Mà GK = 3 cm nên suy ra GH = HI = IK = 3 cm
Vậy độ dài các cạnh còn lại của hình vuông là 3 cm
Xem thêm lý thuyết Toán lớp 3 hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 3 hay khác:
- Giải sgk Toán lớp 3 Chân trời sáng tạo
- Giải vbt Toán lớp 3 Chân trời sáng tạo
- Giải lớp 3 Chân trời sáng tạo (các môn học)
- Giải lớp 3 Kết nối tri thức (các môn học)
- Giải lớp 3 Cánh diều (các môn học)
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Loạt bài Giải bài tập Toán lớp 3 của chúng tôi được biên soạn bám sát nội dung sgk Toán lớp 3 Chân trời sáng tạo (NXB Giáo dục).
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
