Giải Toán 7 trang 92 Tập 2 Cánh diều

Với Giải Toán 7 trang 92 Tập 2 trong Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc Toán 7 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 7 làm bài tập Toán 7 trang 92.

Giải Toán 7 trang 92 Tập 2 Cánh diều

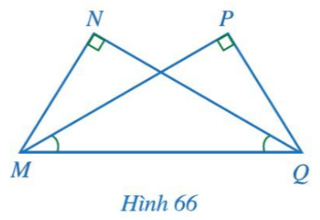
Bài 3 trang 92 Toán lớp 7 Tập 2: Cho Hình 66 có $\hat{N}=\hat{P}=90°,\widehat{PMQ}=\widehat{NQM}.$ Chứng minh MN = QP, MP = QN.

Lời giải:

Tam giác MNQ có $\hat{N}=90°$ nên tam giác MNQ vuông tại N.

Tam giác QPM có $\hat{P}=90°$ nên tam giác QPM vuông tại P.

Xét ∆MNQ vuông tại N và ∆QPM vuông tại P có:

$\widehat{NQM}=\widehat{PMQ}$ (theo giả thiết).

MQ chung.

Suy ra ∆MNQ = ∆QPM (cạnh huyền - góc nhọn).

Do đó MN = QP (2 cạnh tương ứng), MP = QN (2 cạnh tương ứng).

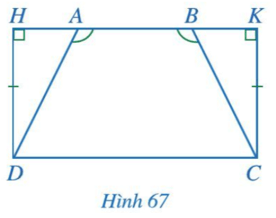
Bài 4 trang 92 Toán lớp 7 Tập 2: Cho Hình 67 có $\widehat{AH\text{D}}=\widehat{BKC}=90°$, DH = CK, $\widehat{DAB}=\widehat{CBA}$. Chứng minh AD = BC.

Lời giải:

Ta thấy $\widehat{DAB}$ là góc ngoài tại đỉnh A của tam giác AHD nên $\widehat{DAB}=\widehat{AHD}+\widehat{A\text{D}H}$ hay

$\widehat{DAB}=90°+\widehat{A\text{D}H}$.

$\widehat{CBA}$ là góc ngoài tại đỉnh B của tam giác BKC nên $\widehat{CBA}=\widehat{BKC}+\widehat{BCK}$ hay $\widehat{CBA}=90°+\widehat{BCK}$.

Mà $\widehat{DAB}=\widehat{CBA}$ nên $\widehat{A\text{D}H}=\widehat{BCK}$.

Xét ∆AHD vuông tại H và ∆BKC vuông tại K có:

$\widehat{A\text{D}H}=\widehat{BCK}$ (chứng minh trên).

DH = CK (theo giả thiết).

Suy ra ∆AHD = ∆BKC (góc nhọn - cạnh góc vuông).

Do đó AD = BC (2 cạnh tương ứng).

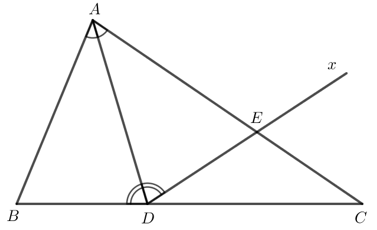
Bài 5 trang 92 Toán lớp 7 Tập 2: Cho tam giác ABC có $\hat{B}>\hat{C}.$ Tia phân giác góc BAC cắt cạnh BC tại điểm D.

a) Chứng minh $\widehat{A\text{D}B}<\widehat{A\text{D}C}$.

b) Kẻ tia Dx nằm trong góc ADC sao cho $\widehat{A\text{Dx}}=\widehat{A\text{D}B}$. Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: ∆ABD = ∆AED, AB < AC.

Lời giải:

a) $\widehat{A\text{D}B}$ là góc ngoài tại đỉnh D của tam giác ADC nên $\widehat{ADB}=\widehat{DAC}+\widehat{AC\text{D}}$.

$\widehat{A\text{D}C}$ là góc ngoài tại đỉnh D của tam giác ADB nên $\widehat{A\text{D}C}=\widehat{DAB}+\widehat{ABD}$.

Do AD là tia phân giác của $\widehat{BAC}$ nên $\widehat{DAB}=\widehat{DAC}$.

Mà $\widehat{AB\text{D}}>\widehat{AC\text{D}}$ nên $\widehat{DAC}+\widehat{AC\text{D}}<\widehat{DAB}+\widehat{ABD}$ hay $\widehat{A\text{D}B}<\widehat{A\text{D}C}$.

b) Xét ∆ABD và ∆AED có:

$\widehat{DAB}=\widehat{DAE}$ (chứng minh trên).

AD chung.

$\widehat{A\text{D}B}=\widehat{A\text{D}E}$ (theo giả thiết).

Suy ra ∆ABD = ∆AED (g - c - g).

Do đó AB = AE.

Mà AE < AC nên AB < AC.

Vậy ∆ABD = ∆AED và AB < AC.

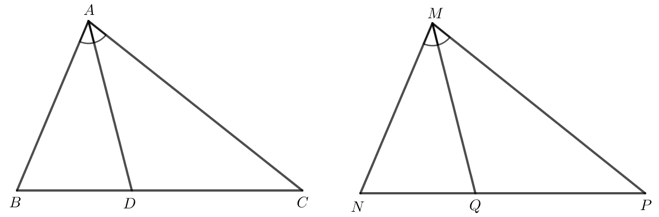
Bài 6 trang 92 Toán lớp 7 Tập 2: Cho ∆ABC = ∆MNP. Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.

Lời giải:

Do ∆ABC = ∆MNP nên $\widehat{BAC}=\widehat{NMP}$ (2 góc tương ứng), $\widehat{ACB}=\widehat{MPN}$ (2 góc tương ứng) và AC = MP (2 cạnh tương ứng).

Do AD là tia phân giác của $\widehat{BAC}$ nên $\widehat{DAC}=\frac{1}{2}\widehat{BAC}$.

Do MQ là tia phân giác của $\widehat{NMP}$ nên $\widehat{QMP}=\frac{1}{2}\widehat{NMP}$.

Mà $\widehat{BAC}=\widehat{NMP}$ nên $\widehat{DAC}=\widehat{QMP}$.

Xét ∆ADC và ∆MQP có:

$\widehat{DAC}=\widehat{QMP}$ (chứng minh trên).

AC = MP (chứng minh trên).

$\widehat{AC\text{D}}=\widehat{MPQ}$ (chứng minh trên).

Suy ra ∆ADC = ∆MQP (g - c - g).

Do đó AD = MQ (2 cạnh tương ứng).

Lời giải bài tập Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc hay khác:

• Giải Toán 7 trang 88 Tập 2

• Giải Toán 7 trang 89 Tập 2

• Giải Toán 7 trang 91 Tập 2

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

• Toán 7 Bài 7: Tam giác cân

• Toán 7 Bài 8: Đường vuông góc và đường xiên

• Toán 7 Bài 9: Đường trung trực của một đoạn thẳng

• Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

• Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác

Xem thêm các tài liệu học tốt lớp 7 hay khác:

• Giải sgk Toán 7 Cánh diều
• Giải SBT Toán 7 Cánh diều
• Giải lớp 7 Cánh diều (các môn học)
• Giải lớp 7 Kết nối tri thức (các môn học)
• Giải lớp 7 Chân trời sáng tạo (các môn học)

---