Giải Toán 10 trang 97 Tập 2 Kết nối tri thức

Với Giải Toán 10 trang 97 Tập 2 trong Bài tập ôn tập cuối năm Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 trang 97.

Giải Toán 10 trang 97 Tập 2 Kết nối tri thức

Bài 17 trang 97 Toán 10 Tập 2: Trong đêm, một âm thanh cầu cứu phát ra từ một vị trí trong rừng và đã được hai trạm ghi tín hiệu ở các vị trí A, B nhận được. Khoảng cách giữa hai trạm là 16 km và trạm ở vị trí A nhận được tín hiệu sớm hơn 6 giây so với trạm ở vị trí B. Giả sử vận tốc âm thanh là 1 236 km/h. Hãy xác định phạm vi tìm kiếm vị trí phát ra âm thanh đó.

Lời giải:

Gọi M là vị trí phát ra âm thanh cầu cứu trong rừng. Gọi t_A, t_B lần lượt là thời gian truyền từ M đến các trạm phát thanh A, B. 

Theo đề bài ta có t_B – t_A = 6 (giây) hay t_A – t_B = – 6 (giây).

Đổi 1 236 km/h = $\frac{1236}{3600}km/s=\frac{103}{300}km/s$. 

Khi đó vận tốc âm thanh là $v=\frac{103}{300}km/s$

Khoảng cách từ M đến A chính là quãng đường âm thanh di chuyển từ M đến A, do đó MA = v . t_A. 

Khoảng cách từ M đến B chính là quãng đường âm thanh di chuyển từ M đến B, do đó MB = v . t_B. 

Từ đó suy ra: MA – MB = v . t_A – v . t_B= v(t_A – t_B) = $\frac{103}{300}.\left(-6\right)=-\frac{103}{50}=-\mathrm{2,06}$. 

Gọi (H) là hypebol ở dạng chính tắc nhận A, B làm hai tiêu điểm và đi qua M. Khi đó ta có $\left\{\begin{array}{l}2c=AB=16\\ 2a=\left|MA-MB\right|=\left|-\mathrm{2,06}\right|=\mathrm{2,06}\end{array}\right.$$\iff \left\{\begin{array}{l}c=8\\ a=\mathrm{1,03}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}a=\mathrm{1,03}\\ b=\sqrt{c^2-a^2}=\sqrt{8^2-{\left(\mathrm{1,03}\right)}^2}=\sqrt{\mathrm{62,9391}}\end{array}\right.$

Vậy phương trình chính tắc của (H) là $\frac{x^2}{{\left(\mathrm{1,03}\right)}^2}-\frac{y^2}{{\left(\sqrt{\mathrm{62,9391}}\right)}^2}=1$ hay $\frac{x^2}{\mathrm{1,0609}}-\frac{y^2}{\mathrm{62,9391}}=1$. 

(Lưu ý rằng MA < MB, do đó vị trí của điểm M thuộc nhánh của (H) gần với trạm A hơn). 

Vậy phạm vi tìm kiếm vị trí phát ra âm thanh đó là hypebol (H) có phương trình $\frac{x^2}{\mathrm{1,0609}}-\frac{y^2}{\mathrm{62,9391}}=1$. 

Bài 18 trang 97 Toán 10 Tập 2: Các nhà toán học cổ đại Trung Quốc đã dùng phân số $\frac{22}{7}$ để xấp xỉ cho π.

a) Cho biết đâu là số đúng, đâu là số gần đúng.

b) Đánh giá sai số tuyệt đối, sai số tương đối của giá trị gần đúng này, biết: 3,1415 < π < 3,1416.

Lời giải:

a) Số đúng là số π, số gần đúng là $\frac{22}{7}$. 

b)Vì 3,1415 < π < 3,1416

Nên – 3,1415 > – π > – 3,1416

$\iff \frac{22}{7}-\mathrm{3,1416}<\frac{22}{7}-\pi <\frac{22}{7}-\mathrm{3,1415}$

Từ đó suy ra: $\left|\frac{22}{7}-\pi \right|<\frac{22}{7}-\mathrm{3,1415}=\mathrm{0,001357142...}<\mathrm{0,0014}$.

Do đó sai tuyệt đối không quá 0,0014 và sai số tương đối nhỏ hơn $\frac{\mathrm{0,0014}}{\frac{22}{7}}<\mathrm{0,05}\%$.  

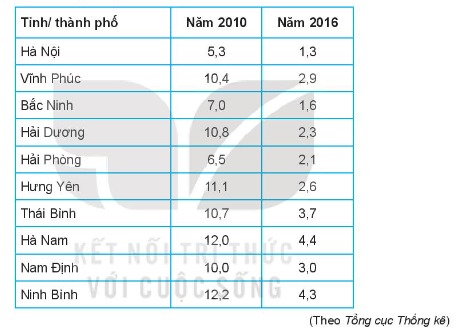
Bài 19 trang 97 Toán 10 Tập 2: Tỉ lệ hộ nghèo (%) của 10 tỉnh/thành phố thuộc đồng bằng sông Hồng trong năm 2010 và năm 2016 được cho trong bảng sau:

a) Tính số trung bình và độ lệch chuẩn của tỉ lệ hộ nghèo các tỉnh/thành phố thuộc đồng bằng sông Hồng trong các năm 2010, 2016.

b) Dựa trên kết quả nhận được, em có nhận xét gì về số trung bình và độ phân tán của tỉ lệ hộ nghèo các tỉnh/thành phố thuộc đồng bằng sông Hồng trong các năm 2010 và 2016.

Lời giải:

a) 

* Năm 2010: 

Tỉ lệ hộ nghèo trung bình là

$\overline{x_1}=\frac{\mathrm{5,3}+\mathrm{10,4}+\mathrm{7,0}+\mathrm{10,8}+\mathrm{6,5}+\mathrm{11,1}+\mathrm{10,7}+\mathrm{12,0}+\mathrm{10,0}+\mathrm{12,2}}{10}=\mathrm{9,6}$. 

Phương sai của mẫu số liệu trên là: 

$s_1^2=\frac{1}{10}$[(5,3 – 9,6)² + (10,4 – 9,6)² + (7,0 – 9,6)² + (10,8 – 9,6)² + (6,5 – 9,6)² + (11,1 – 9,6)² + (10,7 – 9,6)² + (12,0 – 9,6)² + (10,0 – 9,6)² + (12,2 – 9,6)²] = 5,308. 

Độ lệch chuẩn của mẫu số liệu là s₁ = $\sqrt{s_1^2}=\sqrt{\mathrm{5,308}}\approx \mathrm{2,304}$. 

* Năm 2016: 

Tỉ lệ hộ nghèo trung bình là

$\overline{x_2}=\frac{\mathrm{1,3}+\mathrm{2,9}+\mathrm{1,6}+\mathrm{2,3}+\mathrm{2,1}+\mathrm{2,6}+\mathrm{3,7}+\mathrm{4,4}+\mathrm{3,0}+\mathrm{4,3}}{10}=\mathrm{2,82}$. 

Phương sai của mẫu số liệu trên là: 

$s_2^2=\frac{1}{10}$[(1,3 – 2,82)² + (2,9 – 2,82)² + (1,6 – 2,82)² + (2,3 – 2,82)² + (2,1 – 2,82)² + (2,6 – 2,82)² + (3,7 – 2,82)² + (4,4 – 2,82)² + (3,0 – 2,82)² + (4,3 – 2,82)²] = 1,0136. 

Độ lệch chuẩn của mẫu số liệu là s₂ = $\sqrt{s_2^2}=\sqrt{\mathrm{1,0136}}\approx \mathrm{1,007}$. 

b) Nhận xét: 

Dựa theo số trung bình thì tỉ lệ hộ nghèo của các tỉnh/thành phố thuộc đồng bằng sông Hồng của năm 2016 giảm so với năm 2010 (do 2,82 < 9,6). 

Dựa theo độ lệch chuẩn của tỉ lệ hộ nghèo năm 2016 cũng giảm so với năm 2010 (do 1,007 < 2,304), điều đó có nghĩa là mức độ phân tán hay chênh lệch về tỉ lệ hộ nghèo giữa các tỉnh của năm 2016 thấp hơn so với năm 2010.

Bài 20 trang 97 Toán 10 Tập 2: Chọn ngẫu nhiên ba số khác nhau từ 23 số nguyên dương đầu tiên. Tìm xác suất để tổng ba số chọn được là một số chẵn.

Lời giải:

Không gian mẫu Ω là các tập {a; b; c} (với {a; b; c} là tập con của tập các số tự nhiên của đoạn [1; 23]). 

Vậy n(Ω) = $C_{23}^3=1771$.

Gọi biến cố H: “Tổng ba số được chọn là một số chẵn”. 

Ta có H ⊂ Ω là các tập {a; b; c} mà a + b + c chẵn. 

Mà a + b + c chẵn khi và chỉ khi cả 3 số cùng chẵn hoặc có 2 số lẻ và 1 số chẵn. 

Trường hợp 1. Cả ba số được chọn cùng chẵn. Tập các số chẵn thuộc đoạn [1; 23] là A = {2; 4; … ; 22}. Suy ra n(A) = 11. Do đó số tập con {a; b; c} ⊂ A là $C_{11}^3=165$. 

Vậy có 165 bộ ba số {a; b; c} mà cả ba số cùng chẵn. 

Trường hợp 2. Hai số lẻ và một số chẵn. 

Tập các số lẻ thuộc đoạn [1; 23] là B = {1; 3; …; 23}. Suy ra n(B) = 12. 

Chọn 2 số lẻ trong 12 số lẻ có $C_{12}^2=66$ cách chọn. 

Chọn 1 số chẵn trong 11 số chẵn có 11 cách chọn. 

Theo quy tắc nhân, do đó số tập {a; b; c} với 2 số lẻ và 1 số chẵn là 66 . 11 = 726. 

Vậy có 726 bộ ba số {a; b; c} gồm 2 số lẻ và 1 số chẵn. 

Do đó, n(H) = 165 + 726 = 891. 

Vậy xác suất của biến cố H là $P\left(H\right)=\frac{n\left(H\right)}{n\left(\Omega \right)}=\frac{891}{1771}=\frac{81}{161}$. 

Lời giải bài tập Toán 10 Bài tập ôn tập cuối năm hay khác:

• Giải Toán 10 trang 95

• Giải Toán 10 trang 96

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

• Chương 1: Mệnh đề và tập hợp

• Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

• Chương 3: Hệ thức lượng trong tam giác

• Chương 4: Vectơ

• Chương 5: Các số đặc trưng của mẫu số liệu không ghép nhóm

• Hoạt động thực hành trải nghiệm

• Chương 6: Hàm số, đồ thị và ứng dụng

• Chương 7: Phương pháp tọa độ trong mặt phẳng

• Chương 8: Đại số tổ hợp

• Chương 9: Tính xác suất theo định nghĩa cổ điển

• Hoạt động thực hành trải nghiệm

Xem thêm các tài liệu học tốt lớp 10 hay khác:

• Giải sgk Toán 10 Kết nối tri thức
• Giải Chuyên đề học tập Toán 10 Kết nối tri thức
• Giải SBT Toán 10 Kết nối tri thức
• Giải lớp 10 Kết nối tri thức (các môn học)
• Giải lớp 10 Chân trời sáng tạo (các môn học)
• Giải lớp 10 Cánh diều (các môn học)

---