Tổng hợp lý thuyết Chương 1 phần Số học Toán 6 có đáp án

Bài viết Tổng hợp lý thuyết Chương 1 phần Số học Toán 6 lớp 6 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm Tổng hợp lý thuyết Chương 1 phần Số học Toán 6.

Tổng hợp lý thuyết Chương 1 phần Số học Toán 6 có đáp án

A. Lý thuyết

1. Tập hợp

Tập hợp: là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.

2. Cách viết tập hợp

   + Tên tập hợp được viết bằng chữ cái in hoa như: A, B, C,…

   + Để viết tập hợp thường có hai cách viết:

• Liệt kê các phần tử của tập hợp

Ví dụ: A = {0; 1; 2; 3; 4}

• Theo tính chất đặc trưng cho các phần tử của tập hợp đó.

Ví dụ: A = {x ∈ N|x < 5}

   + Kí hiệu:

• 2 ∈ A đọc là 2 thuộc A hoặc là 2 là phần tử của A.

• 6 ∉ A đọc là 6 không thuộc A hoặc là 6 không là phần tử của A.

Chú ý:

• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";" (nếu có phần tử số) hoặc dấu "," nếu không có phần tử số.

• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.

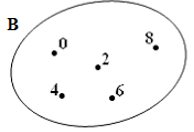
• Ngoài ra ta còn minh họa tập hợp bằng một vòng tròn kín, mỗi phần tử của tập hợp được biểu diễn bằng 1 dấu chấm bên trong vòng tròn kín đó.

Ví dụ: Tập hợp B trong hình vẽ là B = {0; 2; 4; 6; 8}

3. Tập hợp các số tự nhiên

Các số 0; 1; 2; 3... là các số tự nhiên. Tập hợp các số tự nhiên được kí hiệu là N.

Tập hợp các số tự nhiên khác 0 được kí hiệu là N^∗.

Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số. Trên tia số, điểm biểu diễn số nhỏ nằm bên trái điểm biểu diễn số lớn.

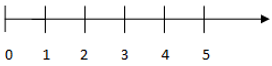
4. Thứ tự trong tập hợp số tự nhiên

   + Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết a < b hoặc b > a

Ngoài ra ta cũng viết a ≥ b để chỉ a < b hoặc a = b, viết a ≤ b để chỉ a < b hoặc a = b

   + Nếu a < b và b < c thì a < c.

   + Hai số tự nhiên liên tiếp nhau hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất.

   + Số 0 là số tự nhiên bé nhất. Không có số tự nhiên lớn nhất.

   + Tập hợp các số tự nhiên có vô số phần tử.

5. Số và chữ số

Để ghi số một trăm chín mốt, ta viết: 191.

Một số tự nhiên có thể có một, hai, ba,…chữ số.

Chú ý:

• Khi viết một số tự nhiên có năm chữ số trở lên, người ta thường viết tách riêng ra thành từng nhóm có 3 chữ số kể từ phải sang trái cho dễ đọc.

Chẳng hạn như:

• Cần phân biệt số với chữ số, số chục với chữ số hàng chục, số trăm với chữ số hàng trăm,…

6. Hệ thập phân

Trong hệ thập phân

   + Để ghi số tự nhiên trong hệ thập phân, người ta thường dùng mười chữ số là: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

   + Trong hệ thập phân, cứ mười đơn vị của một hàng thì làm thành đơn vị của hàng liền trước đó.

7. Số phần tử của một tập hợp

Một tập hợp có thể có một phần tử, có nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào.

Tập hợp không có phần tử được gọi là tập hợp rỗng

Tập hợp rỗng được kí hiệu là ∅.

8. Tập hợp con

Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A được gọi là tập hợp con của tập hợp B.

Kí hiệu: A ⊂ B hoặc B ⊃ A và đọc là: A là tập hợp con của tập hợp B, hoặc A được chứa trong B hoặc B chứa A.

Chú ý:

   + Nếu A ⊂ B và B ⊂ A thì ta nói A và B là hai tập hợp bằng nhau, kí hiệu là A = B.

   + Mỗi tập hợp đều là tập hợp con của chính nó. Quy ước: Tập hợp rỗng là tập hợp con của mọi tập hợp

   + Cách tìm số tập hợp con của một tập hợp là: Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2ⁿ.

   + Giao của hai tập hợp kí hiệu là ∩ là một tập hợp gồm các phần tử chung của hai tập hợp đó.

9. Tổng và tích hai số tự nhiên

Phép cộng:

a + b = c hay có thể hiểu: số hạng + số hạng = tổng.

Phép nhân:

a x b = c hay có thể hiểu: thừa số x thừa số = tích.

10. Tính chất của phép cộng và phép nhân số tự nhiên

Tính chất giao hoán::

Tính chất giao hoán:

   + Khi đổi các số hạng trong một tổng thì tổng không thay đổi.

   + Khi đổi các thừa số trong một tích thì tích đó không thay đổi.

Tính chất kết hợp:

   + Muốn cộng một tổng hai số với một số thứ ba, người ta có thể cộng số thứ nhất với tổng của số thứ hai với số thứ ba.

   + Muốn nhân một tích hai số với một số thứ ba, người ta có thể nhân số thứ nhất với tích của số thứ hai với số thứ ba.

Tính chất phân phối của phép nhân với phép cộng:

   + Muốn nhân một số với một tổng, ta có thể nhân số đó với từng số hạng của tổng, rồi cộng các kết quả lại.

11. Phép trừ hai số tự nhiên

Cho hai số tự nhiên a và b, nếu có số tự nhiên x sao cho b + x = a thì ta có phép trừ a - b = x.

Trong đó: a là số bị trừ, b là số trừ, x là hiệu.

Tổng quát: (số bị trừ) - (số trừ) = hiệu.

Chú ý: Điều kiện để thực hiện phép trừ là số bị trừ lớn hơn hoặc bằng số trừ.

12. Phép chia hết và phép chia có dư

Cho hai số tự nhiên a và b, trong đó b ≠ 0 nếu có số tự nhiên x sao cho b.x = a thì ta nói a chia hết cho b và ta có phép chia hết là a : b = x.

(số bị chia) : (số chia) = thương.

Tổng quát: Cho hai số tự nhiên a và b, trong đó b ≠ 0 ta luôn tìm được hai số tự nhiên là q và r duy nhất sao cho:

a = b.q + r trong đó 0 ≤ r < b

   + Nếu r = 0 thì ta có phép chia hết.

   + Nếu r ≠ 0 thì ta có phép chia có dư

13. Lũy thừa với số mũ tự nhiên

Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.

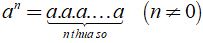
   + a gọi là cơ số.

   + n gọi là số mũ.

Phép nhân nhiều thừa số bằng nhau được gọi là phép nâng lên lũy thừa

Chú ý:

   + a² gọi là a bình phương (hay bình phương của a)

   + a³ gọi là a lập phương (hay lập phương của a)

Quy ước: a¹ = a

14. Nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

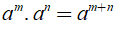
15. Chia hai lũy thừa cùng cơ số

Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ số mũ.

Mọi số tự nhiên đều được viết dưới dạng tổng các lũy thừa của 10.

Quy ước: a⁰ = 1 (a ≠ 0)

16. Thứ tự thực hiện các phép tính trong biểu thức

a) Đối với biểu thức không có dấu ngoặc

   + Nếu phép tính chỉ có cộng, trừ hoặc chỉ có nhân, chia ta thực hiện phép tính theo thứ tự từ trái sang phải.

   + Nếu phép tính có cả cộng, trừ, nhân, chia, nâng lũy thừa, ta thực hiện phép nâng lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.

Lũy thừa → Nhân chia → Cộng trừ

b) Đối với biểu thức có dấu ngoặc

   + Nếu biểu thức có các dấu ngoặc: ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiên phép tính theo thứ tự:

( ) → [ ] → { }

17. Tính chất 1 của phép chia

Nếu và thì

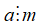
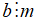
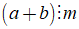
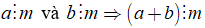
   + Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.

   + Ta có thể viết hoặc đều được.

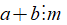
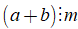
Chú ý:

• Tính chất 1 cũng đúng đối với một hiệu

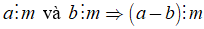
• Tính chất 1 cũng đúng với một tổng nhiều số hạng

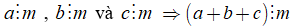
Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

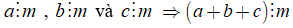
18. Tính chất 2 của phép chia

Nếu và thì

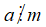
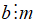
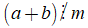
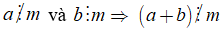
Nếu và thì

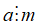
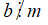
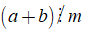
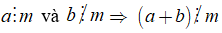
   + Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.

   + Ta có thể viết hoặc đều được.

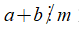
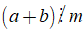
Chú ý:

• Tính chất 2 cũng đúng đối với một hiệu

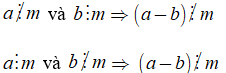
• Tính chất 2 cũng đúng với một tổng nhiều số hạng

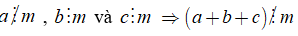
Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số , còn các số hạng còn lại đều chia hết cho số đó thì tổng đó không chia hết cho số đó.

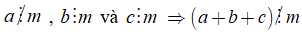
19. Dấu hiệu chia hết cho 2

Dấu hiệu: Các số có chữ số tận cùng là chữ số chẵn thì đều chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

20. Dấu hiệu chia hết cho 5

Dấu hiệu: Các số có chữ số tận cùng là 0 hoặc 5 thì đều chia hết cho 5, chỉ có những số đó mới chia hết cho 5.

21. Dấu hiệu chia hết cho 9

Dấu hiệu: Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó chia hết cho 9.

22. Dấu hiệu chia hết cho 3

Dấu hiệu: Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó chia hết cho 3.

23. Ước và bội

Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b và b là ước của a.

24. Cách tìm ước và bội

• Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lượt với 0, 1, 2, 3,....

• Ta có thể tìm ước của a (a > 1) bằng cách lần lượt chia a cho các số tự nhiên từ 1 đến a để xem xét a chia hết cho những số nào, khi đó các số đó là ước của a.

25. Số nguyên tố. Hợp số:

Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.

Nhận xét:

Cách kiểm tra một số là số nguyên tố: Để kết luận số a là số nguyên tố (a > 1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.

26. Cách phân tích một số ra thừa số nguyên tố:

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố

Ta có thể phân tích theo chiều dọc như sau:

Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Nhận xét: Dù phân tích một số ra thừa số nguyên tố bằng cách nào đi nữa thì cuối cùng cũng ra một kết quả

27. Ước chung

Ước chung của hai hay nhiều số là ước của tất cả các số đó.

Nhận xét:

   + x ∈ UC(a, b) nếu

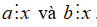
   + x ∈ UC(a, b, c) nếu

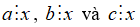
28. Bội chung

Bội chung của hai hay nhiều số là bội của tất cả các số đó.

Nhận xét:

   + x ∈ BC(a, b) nếu

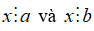
   + x ∈ BC(a, b, c) nếu

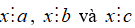
Giao của hai tập hợp là một tập hợp gồm các phần tử chung của hai tập hợp đó.

Kí hiệu: Giao của tập hợp A và tập hợp B kí hiệu là A ∩ B

Có thể hiểu:

   + U(a) ∩ U(b) = UC(a,b)

   + B(a) ∩ B(b) = BC(a,b)

30. Ước chung lớn nhất:

Định nghĩa: Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

Cách tìm Ước chung lớn nhất:

   + Phân tích mỗi số ra thừa số nguyên tố

   + Chọn ra các thừa số nguyên tố chung.

   + Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là UCLN phải tìm

Chú ý:

   + Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.

   + Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhau.

   + Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy

   Cách tìm ước chung thông qua tìm ƯCLN:

   Để tìm ước chung của các số đã cho, ta có thể tìm các ước của ƯCLN của các số đó.

31. Bội chung nhỏ nhất

Định nghĩa: Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Cách tìm Bội chung nhỏ nhất:

   + Phân tích mỗi số ra thừa số nguyên tố.

   + Chọn ra các thừa tố nguyên tố chung và riêng.

   + Lập tích các thừa số đã chọn, mỗi thừa số lấy số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

   Cách tìm bội chung thông qua tìm BCNN:

   Để tìm bội chung của các số đã cho, ta có thể tìm các bội của BCNN của các số đó.

B. Bài tập

Câu 1: Viết các tập hợp sau:

a. A là tập hợp các số tự nhiên chẵn bé hơn 20.

b. B là tập hợp các số tự nhiên không vượt quá 10.

Lời giải:

a. Ta có A là tập hợp các số tự nhiên chẵn bé hơn 20.

⇒ A = {0; 2; 4; 6; 8; 10; 12; 14; 16; 18}

b. Ta có B là tập hợp các số tự nhiên không vượt quá 10.

⇒ B = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}

Câu 2:

a. Số liền trước số 49 là số?

b. Tìm các số tự nhiên a, b, c thỏa mãn 228 ≤ a < b < c ≤ 230?

Lời giải:

a. Số liền trước số 49 là số 48.

b. Theo đề bài, ta có các số tự nhiên lớn hơn hoặc bằng 228 và nhỏ hơn hoặc bằng 230 là 228; 229; 230.

Mà mặt khác a < b < c nên a = 228; b = 229; c = 230.

Câu 3: Thực hiện các phép tính sau

a. 3⁷.27.81

b. 100.1000.10000

Lời giải:

a. Ta có: 3⁷.27.81 = 3⁷.3³.3⁴ = 3⁷⁺³⁺⁴ = 3¹⁴

b. Ta có: 100.1000.10000 = 10².10³.10⁴ = 10².10³.10⁴ = 10²⁺³⁺⁴ = 10⁹

Câu 4: Cho số N = 5a27b−−−−−−−−−−−−. Có bao nhiêu số N sao cho N là số có 5 chữ số khác nhau và N chia cho 3 dư 2, N chia cho 5 dư 1 và N chia hết cho 2.

Lời giải:

Điều kiện: a, b ∈ {0; 1; 2; 3; ....; 9}

N = 5a27b−−−−−−−−−−−− chia cho 5 dư 1 ⇒ b ∈ {1; 6}

Mà N chia hết cho 2 nên b = 6, ta được số N = 5a27b−−−−−−−−−−−−

Vì N chia 3 dư 2 nên 5 + a + 2 + 7 + 6 = 20 + a chia 3 dư 2 ⇒ (18 + a) ⋮ 3

Mà 18 ⋮ 3 nên a ⋮ 3 ⇒ a ∈ {0; 3; 6; 9} (a là chữ số)

Lại có N là số có 5 chữ số khác nhau nên a ∈ {0; 3; 9}

Vậy có 3 số N thỏa mãn yêu cầu bài là 50276; 53276; 59276

Câu 5: Chứng tỏ rằng với mọi số tự nhiên n thì tích (n + 3)(n + 6) chia hết cho 2.

Lời giải:

Với mọi n ta có thể viết hoặc n = 2k + 1 hoặc n = 2k

     + Với n = 2k + 1 ta có: (n + 3)(n + 6) = (2k + 1 + 3)(2k + 1 + 6) = (2k + 4)(2k + 7)

     = 2(k + 2)(2k + 7) chia hết cho 2.

     + Với n = 2k ta có: (n + 3)(n + 6) = (2k + 3)(2k + 6)

     = 2(2k + 3)(k + 3) chia hết cho 2.

Vậy với mọi n ∈ N thì (n + 3)(n + 6) chia hết cho 2.

Câu 6: Một căn phòng hình chữ nhật có chiều dài là 680cm và chiều rộng là 480cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch đó có độ dài lớn nhất bằng bao nhiêu?

Lời giải:

Ta có:

Gọi độ dài của viên gạch hình vuông là x.

Để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì x phải là ước chung của chiều dài và chiều rộng.

Hay 680 ⋮ x và 480 ⋮ x ⇒ x ∈ ƯC(680; 480)

Để x lớn nhất thì ⇒ x = ƯCLN(680; 480)

Ta có: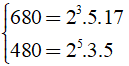

⇒ x = ƯCLN(680; 480) = 2³.5 = 40

Vậy để lát kín căn phòng đó mà không có viên gạch nào bị cắt xén thì độ dài lớn nhất của viên gạch là 40cm

Câu 7: Một khu đất hình chữ nhất có chiều dài là 60cm, chiều rộng là 24cm. Người ta chia thành những thửa đất hình vuông bằng nhau, để mỗi thửa đất có diện tích lớn nhất thì độ dài mỗi cạnh của thửa đất đó bằng?

Lời giải:

Gọi độ dài cạnh của mỗi thửa đất hình vuông là x (cm)

Để diện tích của một thửa đất đó lớn nhất thì độ dài x lớn nhất.

Vì các thửa đất đó được chia ra từ khu đất hình chữ nhật có chiều dài là 60cm, chiều rộng là 24cm

Nên x phải là ước của 60 và 24 hay x ∈ ƯC(24; 60)

Khi đó x lớn nhất thì x = ƯCLN(24; 60)

Ta có: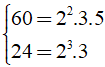

⇒ ƯCL(24; 60) = 2².3 = 12

Vậy mỗi thừa đất hình vuông có độ dài cạnh lớn nhất là 12cm

Câu 8: Tổng của hai số tự nhiên gấp 3 lần hiệu của chúng. Tìm thương của hai số tự nhiên đó?

Lời giải:

Gọi hai số tự nhiên đã cho là a và b (a > b)

Ta có: a + b = 3(a - b)

Nên a + b = 3a - 3b ⇒ 2a = 4b tức là a = 2b

Do đó a:b = 2

Vậy a:b = 2.

Câu 9: Chứng minh A là một lũy thừa của 2 với A = 4 + 2² + 2³ + .... + 2²⁰

Lời giải:

Ta có: A = 4 + 2² + 2³ + .... + 2²⁰

2A = 8 + 2³ + 2⁴ + 2⁵ + .... + 2²¹

Suy ra: 2A - A = 2²¹ + 8 - (2² + 4) = 2²¹

⇒ (đpcm)

Câu 10: Cho số abc−−−−−−−−−− chia hết cho 27. Chứng minh rằng số bca−−−−−−−−−− chia hết cho 27

Lời giải:

Ta có: abc−−−−−−−−−− ⋮ 27

⇒ abc0−−−−−−−−−− ⋮ 27

⇒ 1000a + bc0−−−−−−−−−− ⋮ 27

⇒ 999a + a + bc0−−−−−−−−−− ⋮ 27

⇒ 27.37a + bca−−−−−−−−−− ⋮ 27

Do 27.37a ⋮ 27 nên bca−−−−−−−−−− chia hết cho 27

⇒ (đpcm)

Câu 11: Viết số 108 dưới dạng tổng các số tự nhiên liên tiếp lớn hơn 0.

Lời giải:

Giả sử số 108 được viết dưới dạng tổng của k số tự nhiên liên tiếp là n + 1; n + 2; ....; n + k với k, n ∈ N, k ≥ 2, n+1 ≥ 1

Ta có: (n + 1) + (n + 2) + ... + (n + k) = 108

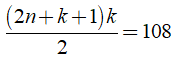
    (2n + k + 1)k = 216

Bài toán đưa về tìm các ước của 216. Ta đưa ra các nhận xét sau để giảm bớt các trường hợp phải xét:

    + 2n + k + 1 > k ≥ 2

    + Hiệu (2n + k + 1) - k = 2n + 1 là số lẻ nên trong hai số của hiệu thì có một số là số lẻ, có một số là số chẵn.

Do đó ta chỉ cần tìm ước lẻ của 216 đồng thời (2n + k + 1)k = 216

Phân tích 216 ra thừa số nguyên tố là 216 = 2³.3³

Ước lẻ của 216 lớn hơn 1 là 3, 9, 27

    + Với k = 3 thì 2n + k + 1 = 72 ta được n = 34

Do đó: 108 = 35 + 36 + 37

    + Với k = 9 thì 2n + k + 1 = 24 ta được n = 7

Do đó: 108 = 8 + 9 + 10 + ... + 16

    + Với 2n + k + 1 = 27 thì k = 8, ta được n = 9

Do đó: 108 = 10 + 11 + 12 + ... + 17

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 6 có đáp án chi tiết hay khác:

• Lý thuyết Bội chung nhỏ nhất
• Bài tập Ước chung lớn nhất. Bội chung nhỏ nhất
• Lý thuyết Làm quen với số âm
• Bài tập Làm quen với số âm
• Lý thuyết Tập hợp các số nguyên
• Bài tập Tập hợp các số nguyên

Xem thêm các loạt bài Để học tốt Toán lớp 6 hay khác:

• Giải bài tập sgk Toán 6
• Giải sách bài tập Toán 6
• Top 52 Đề thi Toán 6 có đáp án

---