Cách giải bài tập về khoảng cách giữa hai phần tử trên phương truyền sóng (hay, chi tiết)

Bài viết Cách giải bài tập về khoảng cách giữa hai phần tử trên phương truyền sóng với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Cách giải bài tập về khoảng cách giữa hai phần tử trên phương truyền sóng.

Cách giải bài tập về khoảng cách giữa hai phần tử trên phương truyền sóng (hay, chi tiết)

Câu 1: M và N là hai điểm trên một mặt nước phẳng lặng cách nhau 1 khoảng 20 cm. Tại 1 điểm O trên đường thẳng MN và nằm ngoài đoạn MN, người ta đặt nguồn dao động theo phương vuông góc với mặt nước với phương trình u = 4cosωt (cm), tạo ra sóng trên mặt nước với bước sóng λ = 15cm. Khoảng cách xa nhất giữa 2 phần tử môi trường tại M và N khi có sóng truyền qua là bao nhiêu?

A. 13cm.    B. 8√7 cm .    C. 19cm.    D.17cm.

Lời giải:

Chọn B

Khoảng cách cực tiểu giữa M và N là: l_min = MN = 20cm.

Giả sử sóng truyền qua M rồi đến N thì dao động tại M sớm pha hơn dao động tại N: Δφ = 2πd/λ = 8π/3.

Chọn gốc thời gian để phương trình dao động tại M là: u₁ = 5cosωt cm thì phương trình dao động tại N là: u₂ = 4cos(ωt - 8π/3 ) cm.

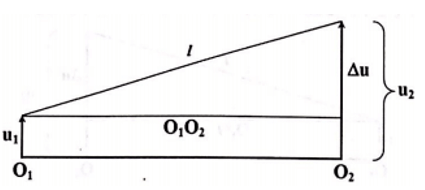
Độ lệch li độ của hai phần tử tại M và tại N:

Δu = u₂ - u₁ = 4cos(ωt - 8π/3 ) - 4cos(ωt) = 4√3 cos (ωt - 5π/6) cm

=> Δφ_u = 4√3

Khoảng cách xa nhất giữa hai phần tử tại M và N:

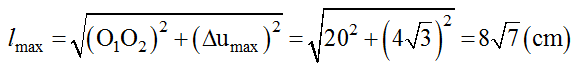
Câu 2: M và N là hai điểm trên một mặt nước phẳng lặng cách nhau một khoảng 12 cm. Tại một điểm O trên đường thẳng MN và nằm ngoài đoạn MN, người ta đặt nguồn dao động theo phương vuông góc với mặt nước với phương trình u = 2,5√2 cos(20πt) , tạo ra sóng trên mặt nước với tốc độ truyền sóng v = 1,6m/s. Coi biên độ sóng trên môi trường không thay đổi theo khoảng cách tới nguồn sóng, khoảng cách xa nhất giữa 2 phần tử môi trường tại M và N khi có sóng truyền qua là:

A. 13 cm.     B. 15,5 cm.    C. 19 cm.     D. 17 cm.

Lời giải:

Chọn A

Bước sóng: λ = v/f = 160/10 = 16cm.

Độ lệch pha giữa hai điểm M, N: Δφ = 2πd/λ = 3π/2 .

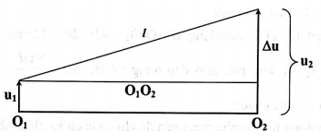
Độ lệch li độ của hai phần tử tại M và tại N:

Δu = u_N - u_M = 2,5√2cos(20πt) - 2,5√2 cos(20πt + 3π/2) = 5 cos (20πt + π/4) cm

=> Δφ_u = 4√3

→ ∆umax = 5cm.

Khoảng cách xa nhất giữa hai phần tử tại M và N:

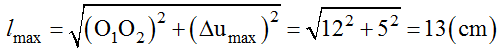
Câu 3: Sóng dọc lan truyền trong một môi trường với bước sóng 15 cm với biên độ không đổi A = 5√3 cm . Gọi M và N là hai điểm cùng nằm trên một phương truyền sóng mà khi chưa có sóng truyền đến lần lượt cách nguồn các khoảng 20 cm và 30 cm. Khoảng cách xa nhất và gần nhất giữa 2 phần tử môi trường tại M và N khi có sóng truyền qua là bao nhiêu?

A. l_max = 11,5cm, l_min = 8,5cm    B. l_max = 20cm, l_min = 0cm

C. l_max = 15cm, l_min = 5cm    D. l_max = 14cm, l_min = 5cm

Lời giải:

Chọn A

Giả sử sóng truyền qua M rồi đến N thì dao động tại M sớm pha hơn dao động tại N: Δφ = 2πMN/λ = 4π/3

Chọn lại gốc thời gian để phương trình dao động tại M là: u₁ = 5√3 cos ωt (mm) thì phương trình dao động tại N là u₂ = 5√3 cos (ωt - 4π/3) mm .

Độ lệch li độ của hai phần tử tại M và tại N:

Δu = u₂ - u₁ = 5√3cos(ωt - 4π/3) - 5√3 cos(ωt) = 15 cos (ωt + 5π/6) cm

→ ∆umax = 15mm = 1,5cm < MN.

Vì đây là sóng dọc nên khoảng cách xa nhất và gần nhất giữa hai phần tử tại M và N:

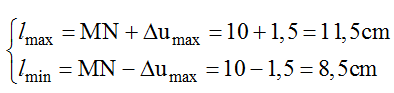
Câu 4: Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số 20 Hz, biên độ 4cm có tốc độ 12 m/s. Gọi A và B là hai điểm nằm trên Ox, ở cùng một phía so với O và cách nhau 15cm. Nếu là sóng ngang thì hai phần tử môi trường tại A và B cách nhau đoạn lớn nhất là

A. 26cm.    B. 15cm    C. √257 cm    D. 10√5 .

Lời giải:

Chọn C

Bước sóng: λ = v/f = 12/20 = 0,6m = 60cm.

Giả sử sóng truyền qua A rồi mới đến B thì dao động tại A sớm hơn dao động tại B: Δφ = 2πAB/λ = π/2

Độ lệch li độ của hai phần tử tại M và tại N:

Δu = u_B - u_A = 4cos(40πt) - 4cos(40πt + π/2) = 4√2 cos (20πt - π/4) cm

=> Δu_max = 4√2 cm

Khoảng cách xa nhất giữa hai phần tử tại A và B:

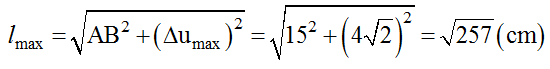
Câu 5: Sóng dọc lan truyền trong một môi trường với tần sốf = 50Hz, tốc độ truyền sóng v = 200cm/s và biên độ không đổi A = 2cm. Gọi A và B là hai điểm cùng nằm trên một phương truyền sóng mà khi chưa có sóng truyền đến lần lượt cách nguồn các khoảng 20 cm và 42 cm. Khi có sóng truyền qua khoảng cách cực đại giữa A và B là bao nhiêu?

A. 26cm    B. 28cm    C. 21cm    D. 10√5 cm

Lời giải:

Chọn A

Bước sóng: λ = v/f = 4cm

Khoảng cách khi chưa dao động: ∆x = AB = 42 – 20 = 22cm

Dao động tại A sớm pha hơn dao động tại B: Δφ = 2πd/λ = 2π.22/4 = 11π (hai dao động này ngược pha nhau).

Độ lệch li độ của hai phần tử tại A và tại B:

Δu = u_A - u_B = 2cos(100πt) - 2cos(100πt - π) = 4 cos (100πt ) cm

→ ∆u_max = 4cm.

Khoảng cách xa nhất giữa hai phần tử tại A và B:

l_max = ∆x + ∆u_max = 22 + 4 = 26 cm

Câu 6: Sóng dọc lan truyền một môi trường với tần số f = 50Hz, tốc độ truyền sóng v = 200cm/s và biên độ không đổi A = 2cm. Gọi A và B là hai điểm cùng nằm trên một phương truyền sóng mà khi chưa có sóng truyền đến lần lượt cách nguồn các khoảng 20 cm và 42 cm. Khi có sóng truyền qua khoảng cách cực tiểu giữa A và B là bao nhiêu?

A. 20cm     B. 26cm     C. 18cm    D. 10√ cm

Lời giải:

Chọn C

Bước sóng: λ = v/f = 4cm

Khoảng cách khi chưa dao động: ∆x = AB = 42 – 20 = 22cm.

Dao động tại A sớm pha hơn dao động tại B: Δφ = 2πd/λ = 2π.22/4 = 11π (hai dao động này ngược pha nhau).

Độ lệch li độ của hai phần tử tại A và tại B:

Δu = u_A - u_B = 2cos(100πt) - 2cos(100πt - π) = 4 cos (100πt ) cm

→ ∆u_max = 4cm.

Khoảng cách xa nhất giữa hai phần tử tại A và tại B:

l_mix = ∆x - ∆u_max = 22 - 4 = 18 cm

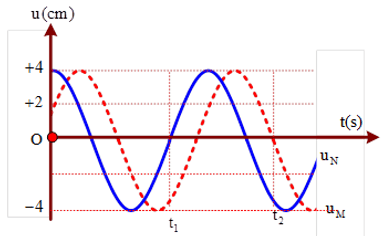
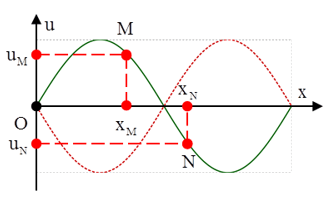
Câu 7: Sóng ngang có tần số f truyền trên một sợi dây đàn hồi rất dài, với tốc độ 3 m/s. Xét hai điểm M và N trên cùng một phương truyền sóng, cách nhau một khoảng x nhỏ hơn một bước sóng, sóng truyền từ N đến M. Đồ thị biểu diễn li độ sóng của M và N cùng theo thời gian t như hình vẽ. Biết t₁ = 0,05 s. Tại thời điểm t₂ , khoảng cách giữa hai phần tử chất lỏng tại M và N có giá trị gần giá trị nào nhất sau đây?

A. 4,8 cm.    B. 6,7 cm.    C. 3,3 cm    D. 3,5 cm.

Lời giải:

Chọn A

Từ đồ thị ta tìm được phương trình dao động của hai phần tử M, N là:

Ta thấy rằng một chu kỳ T chiếm 4 ô đơn vị trên đồ thị, khoảng thời gian t1 = 0,05s chiếm 3 ô đơn vị, do đó ta có: 3/4T = 0,05 => T = 1/15s => ω = 30π rad/s

Độ lệch pha giữa hai dao động sóng tại M và N là:

Δφ = π/3 = 2πx/λ

=> x = x_M - x_N = λ/6 = v.T/6 = 10/3 cm

Thời điểm t₂ = T + 5/12T = 17/180s khi đó điểm M đang có li độ u_M = 0 và li độ của điểm N là:

u_N = 4 cos (ωt) = 4 cos (30π.17/180) = -2√3 cm

Khoảng cách giữa hai phần tử MN:

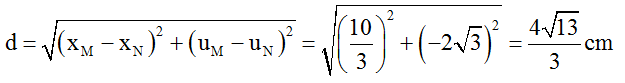
Câu 8: Một sóng ngang lan truyền trong một môi trường đàn hồi với tần số 50 Hz, tốc độ truyền sóng là 2 m/s, biên độ sóng không đổi theo phương truyền sóng là 4 cm. Biết A và B là hai điểm trên cùng một phương truyền sóng. Khi chưa có sóng truyền khoảng cách từ nguồn phát sóng đến hai điểm A và B lần lượt là 20 cm và 42 cm. Khi có sóng truyền qua, khoảng cách lớn nhất giữa hai điểm này là

A. 32 cm    B. 28,4 cm    C. 23,4 cm    D. 30 cm

Lời giải:

Chọn C

Bước sóng của sóng: λ = v/f = 4cm

Phương trình dao động tại hai điểm M và N là:

u_M = 4cos(100πt - 10π) cm;

u_N = 4cos(100πt - 21π) cm;

Khoảng cách giữa hai điểm M và N

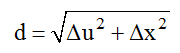
d_max khi ∆u = (u₁ – u₂)max = 8cm. Vậy d_max = 23,4 cm

Câu 9: Một nguồn phát sóng dao động điều hòa theo phương thẳng đứng với tần số f = 4Hz tạo ra sóng tròn đồng tâm tại O truyền trên mặt chất lỏng có tốc độ 0,2 m/s. Hai điểm M và N thuộc mặt chất lỏng mà phần tử tại N dao động cùng pha với phần tử chất lỏng tại O còn phần tử M dao động ngược pha với phần tử dao động tại O. Không kể phần tử chất lỏng tại O, số phần tử chất lỏng dao động cùng pha với phần tử chất lỏng tại O trên đoạn MO là 8, trên đoạn NO là 5 và trên MN là 4. Khoảng cách lớn nhất giữa hai điểm M và N có giá trị gần giá trị nào nhất sau đây?

A. 32 cm    B. 34 cm    C. 15 cm    D. 17 cm

Lời giải:

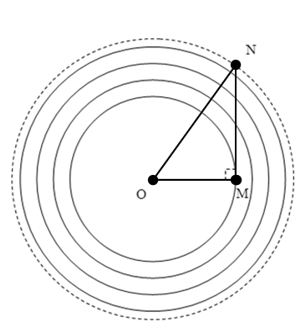
Chọn B

Các đường tròn biểu diễn các điểm cùng pha với nguồn.

M nằm trên đỉnh sóng thứ 6 kể từ nguồn sóng O, N nằm trên điểm ngược pha gần nhất so với đỉnh sóng thứ 9 kể từ O, vậy ON = 8,5λ; ON = 5λ

Từ hình vẽ ta thấy rằng, với điều kiện để trên MN có 4 điểm cùng pha với O thì rõ ràng MN lớn nhất khi MN vuông góc với OM

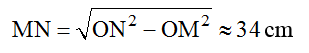
Câu 10: Một sóng ngang truyền trên sợi dây với tốc độ và biên độ không đổi, bước sóng 60 cm. Hai phần tử sóng M, N có vị trí cân bằng cách nhau 10 cm. Tại một thời điểm ly độ của M, N đối nhau và chúng cách nhau 12,5 cm. Biên độ sóng là

A. 2,5 cm     B. 12,5 cm     C. 7,5 cm     D. 5 cm

Lời giải:

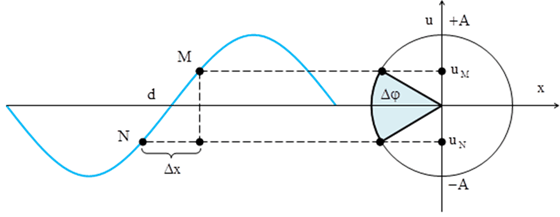
Chọn C

+ Ta có: d² = ∆x² + (2x)² ↔ 12,5² = 10² + (2x)² → x = 3,75cm

+ Độ lệch pha giữa hai phần tử: Δφ = 2πd/λ = 2π10/60 = π/3

Từ hình vẽ ta thấy rằng A = 2u_M = 2.3,75 = 7,5cm

Xem thêm các dạng bài tập Vật Lí lớp 12 có trong đề thi THPT Quốc gia khác:

• Dạng 1: Xác định các đại lượng đặc trưng của sóng

• Dạng 2: Cách viết phương trình sóng

• Tổng hợp Lý thuyết Sóng cơ là gì, ngắn gọn, chi tiết, đầy đủ
• Cách giải Bài tập xác định li độ, vận tốc, trạng thái của phần tử trong Sóng cơ
• Bài tập Đại cương về sóng cơ trong đề thi Đại học (có lời giải)

---