Tìm kiếm theo chiều rộng trong C

Sau khi đã theo dõi phần giải thuật trong chương trước, trong chương này chúng ta sẽ cùng tìm hiểu phần triển khai code trong ngôn ngữ C của giải thuật Tìm kiếm theo chiều rộng.

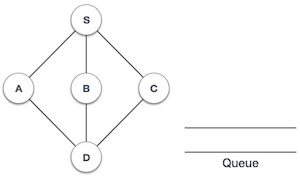
Tìm kiếm theo chiều rộng trong C

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX 5

struct Vertex {
   char label;
   bool visited;
};

//khai bao cac bien cho hang doi (queue)

int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;

//khai bao cac bien cho do thi (graph)

//khai bao danh sach cac dinh (vertex)
struct Vertex* lstVertices[MAX];

//khai bao mot ma tran ke (adjacency matrix)
int adjMatrix[MAX][MAX];

//mot bien de dem so dinh (vertex)
int vertexCount = 0;


//cac ham thao tac tren hang doi (queue)

void insert(int data) {
   queue[++rear] = data;
   queueItemCount++;
}

int removeData() {
   queueItemCount--;
   return queue[front++]; 
}

bool isQueueEmpty() {
   return queueItemCount == 0;
}

//cac ham thao tac tren do thi (graph)

//them dinh vao danh sach cac dinh
void addVertex(char label) {
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

//them canh vao mang cac canh
void addEdge(int start,int end) {
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

//hien thi cac dinh
void displayVertex(int vertexIndex) {
   printf("%c ",lstVertices[vertexIndex]->label);
}       

//lay dinh chua duyet tu ma tran ke
int getAdjUnvisitedVertex(int vertexIndex) {
   int i;
	
   for(i = 0; i<vertexCount; i++) {
      if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
         return i;
   }
	
   return -1;
}

void breadthFirstSearch() {
   int i;

   //danh dau nut dau tien (first node) la da duyet (visited)
   lstVertices[0]->visited = true;

   //hien thi dinh
   displayVertex(0);   

   //chen chi muc cua dinh vao trong hang doi
   insert(0);
   int unvisitedVertex;

   while(!isQueueEmpty()) {
      //Rut dinh chua duoc duyet tu hang doi
      int tempVertex = removeData();   

      //khong tim thay dinh lien ke
      while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
		
   }   

   //hang doi la trong, hoan thanh tim kiem, reset gia tri cua visited        
   for(i = 0;i<vertexCount;i++) {
      lstVertices[i]->visited = false;
   }    
}

int main() {
   int i, j;

   for(i = 0; i<MAX; i++) { // thiet lap cac gia tri
      for(j = 0; j<MAX; j++) // cua ma tran ke la 0
         adjMatrix[i][j] = 0;
   }

   addVertex('S');   // 0
   addVertex('A');   // 1
   addVertex('B');   // 2
   addVertex('C');   // 3
   addVertex('D');   // 4
 
   addEdge(0, 1);    // S - A
   addEdge(0, 2);    // S - B
   addEdge(0, 3);    // S - C
   addEdge(1, 4);    // A - D
   addEdge(2, 4);    // B - D
   addEdge(3, 4);    // C - D
	
   
   printf("\nTim kiem theo chieu rong: ");
   
   breadthFirstSearch();

   return 0;
}

Kết quả

Biên dịch và chạy chương trình C trên sẽ cho kết quả:

Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.

Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:

Follow fanpage của team https://www.facebook.com/vietjackteam/ hoặc facebook cá nhân Nguyễn Thanh Tuyền https://www.facebook.com/tuyen.vietjack để tiếp tục theo dõi các loạt bài mới nhất về Java,C,C++,Javascript,HTML,Python,Database,Mobile.... mới nhất của chúng tôi.