Giải thuật tìm kiếm nhị phân (Binary Search)

Giải thuật tìm kiếm nhị phân (Binary Search) là gì ?

Binany Search (Tìm kiếm nhị phân) là một giải thuật tìm kiếm nhanh với độ phức tạp thời gian chạy là Ο(log n). Giải thuật tìm kiếm nhị phân làm việc dựa trên nguyên tắc chia để trị (Divide and Conquer). Để giải thuật này có thể làm việc một cách chính xác thì tập dữ liệu nên ở trong dạng đã được sắp xếp.

Binary Search tìm kiếm một phần tử cụ thể bằng cách so sánh phần tử tại vị trí giữa nhất của tập dữ liệu. Nếu tìm thấy kết nối thì chỉ mục của phần tử được trả về. Nếu phần tử cần tìm là lớn hơn giá trị phần tử giữa thì phần tử cần tìm được tìm trong mảng con nằm ở bên phải phần tử giữa; nếu không thì sẽ tìm ở trong mảng con nằm ở bên trái phần tử giữa. Tiến trình sẽ tiếp tục như vậy trên mảng con cho tới khi tìm hết mọi phần tử trên mảng con này.

Cách Binary Search làm việc

Để Binary Search làm việc thì mảng phải cần được sắp xếp. Để tiện cho việc theo dõi, mình sẽ cung cấp thêm các hình minh họa tương ứng với mỗi bước.

Giả sử chúng ta cần tìm vị trí của giá trị 31 trong một mảng bao gồm các giá trị như hình dưới đây bởi sử dụng Binary Search:

Đầu tiên, chúng ta chia mảng thành hai nửa theo phép toán sau:

chỉ-mục-giữa = ban-đầu + (cuối + ban-đầu)/ 2

Với ví dụ trên là 0 + (9 – 0)/ 2 = 4 (giá trị là 4.5). Do đó 4 là chỉ mục giữa của mảng.

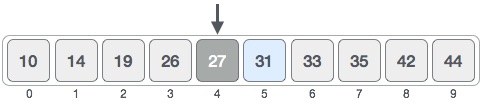
Bây giờ chúng ta so sánh giá trị phần tử giữa với phần tử cần tìm. Giá trị phần tử giữa là 27 và phần tử cần tìm là 31, do đó là không kết nối. Bởi vì giá trị cần tìm là lớn hơn nên phần tử cần tìm sẽ nằm ở mảng con bên phải phần tử giữa.

Chúng ta thay đổi giá trị ban-đầu thành chỉ-mục-giữa + 1 và lại tiếp tục tìm kiếm giá trị chỉ-mục-giữa.

ban-đầu = chỉ-mục-giữa + 1
chỉ-mục-giữa = ban-đầu + (cuối + ban-đầu)/ 2

Bây giờ chỉ mục giữa của chúng ta là 7. Chúng ta so sánh giá trị tại chỉ mục này với giá trị cần tìm.

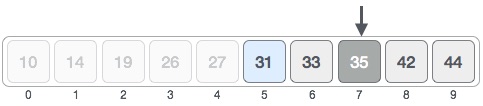
Giá trị tại chỉ mục 7 là không kết nối, và ngoài ra giá trị cần tìm là nhỏ hơn giá trị tại chỉ mục 7 do đó chúng ta cần tìm trong mảng con bên trái của chỉ mục giữa này.

Tiếp tục tìm chỉ-mục-giữa lần nữa. Lần này nó có giá trị là 5.

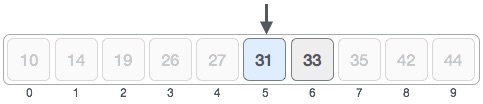
So sánh giá trị tại chỉ mục 5 với giá trị cần tìm và thấy rằng nó kết nối.

Do đó chúng ta kết luận rằng giá trị cần tìm 31 được lưu giữ tại vị trí chỉ mục 5.

Binary Search chia đôi lượng phần tử cần tìm và do đó giảm số lượng phép so sánh cần thực hiện nên giải thuật tìm kiếm này được thực hiện khá nhanh.

Giải thuật mẫu cho Binary Search

Dưới đây là code mẫu cho giải thuật tìm kiếm nhị phân:

Giải thuật tìm kiếm nhị phân (Binary Search)
   A ← một mảng đã được sắp xếp
   n ← kích cỡ mảng
   x ← giá trị để tìm kiếm trong mảng

   gán lowerBound = 1
   gán upperBound = n 

   while x not found
   
      if upperBound < lowerBound 
         EXIT: x không tồn tại.
   
      gán midPoint = lowerBound + ( upperBound - lowerBound ) / 2
      
      if A[midPoint] < x
         gán lowerBound = midPoint + 1
         
      if A[midPoint] > x
         gán upperBound = midPoint - 1 

      if A[midPoint] = x 
         EXIT: x được tìm thấy tại midPoint

   kết thúc while
   
kết thúc giải thuật

Để tìm hiểu sự triển khai code đầy đủ của giải thuật tìm kiếm nhị phân trong ngôn ngữ C, mời bạn click chuột vào chương: Tìm kiếm nhị phân (Binary Search) trong C.

Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.

Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:

Follow fanpage của team https://www.facebook.com/vietjackteam/ hoặc facebook cá nhân Nguyễn Thanh Tuyền https://www.facebook.com/tuyen.vietjack để tiếp tục theo dõi các loạt bài mới nhất về Java,C,C++,Javascript,HTML,Python,Database,Mobile.... mới nhất của chúng tôi.