Giải Toán 7 VNEN Bài 8: Các trường hợp bằng nhau của tam giác vuông

Giải Toán 7 VNEN Bài 8: Các trường hợp bằng nhau của tam giác vuông

A. Hoạt động khởi động

Câu 1: (trang 143 toán 7 VNEN tập 1). Sgk

Câu 2: (trang 144 toán 7 VNEN tập 1). Hãy viết kí hiệu thể hiện sự bằng nhau của các cặp tam giác vuông có trên hình 127. Giải thích vì sao.

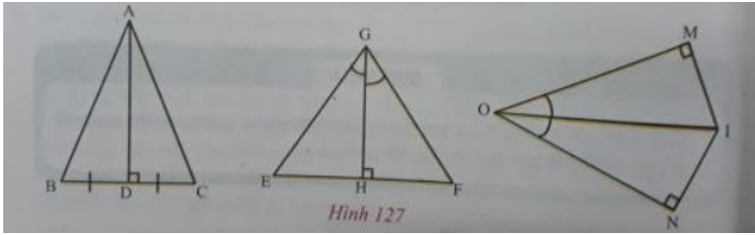
Lời giải:

+ △ADB = △ADC (hai cạnh góc vuông) vì có: AD chung, BD = DC (giả thiết);

+ △GEH = △GFH (cạnh góc vuông – góc nhọn kề cạnh đó) vì có: GH chung, 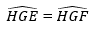(giả thiết);

+ △OIN = △OIM (cạnh huyền – góc nhọn) vì có: OI chung, 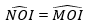(giả thiết);

Câu 3: (trang 144 toán 7 VNEN tập 1) Quan sát hình 128 và đọc ví dụ sau

B. Hoạt động hình thành kiến thức

Câu 1: (trang 144 toán 7 VNEN tập 1). a) Đọc kĩ nội dung sau (sgk trang 144)

b) Cho △ABC cân tại A. Kẻ AH vuông góc với BC (h.130). Chứng minh rằng △AHB = △AHC (giải bằng hai cách).

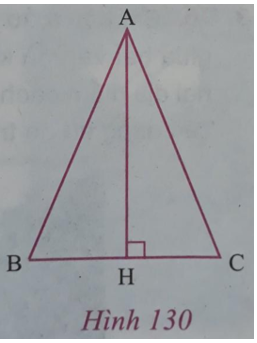
Lời giải:

Gợi ý:

Cách 1: (sgk trang 145)

Trả lời:

Cách 2:

Xét △AHB và △AHC có:

AB = AC (giả thiết);

(do tam giác ABC cân tại A);

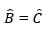
⇒ △AHB = △AHC (cạnh huyền – góc nhọn);

C. Hoạt động luyện tập

Câu 1: (trang 145 toán 7 VNEN tập 1). Cho hai tam giác vuông là ABC và DEF có 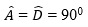, AC = DF. Hãy bổ sung thêm một điều kiện (về cạnh hay về góc) để △ABC = △DEF.

Lời giải:

Để △ABC = △DEF ta có thể bổ sung một trong cách điều kiện sau:

+ AB = DE (theo trường hợp hai cạnh góc vuông);

+ (theo trường hợp cạnh góc vuông – góc nhọn kề cạnh đó);

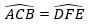
+ BC = EF (theo trường hợp cạnh huyền – cạnh góc vuông);

Câu 2: (trang 145 toán 7 VNEN tập 1). Cho tam giác ABC cân tại A 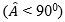. Vẽ BH vuông góc với AC (H thuộc AC), CK vuông góc với AB (K thuộc AB).

a) Chứng minh rằng BH = CK.

b) Gọi I là giao điểm của BH và CK. Chứng minh AI là phân giác của góc A.

c) Lấy M là trung điểm của HK. Chứng minh rằng A, M, I thẳng hàng.

Lời giải:

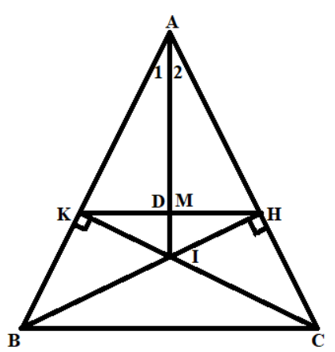
Xét △ABH và △ACK vuông tại H và K có:

AB = AC (do △ABC cân tại A);

chung;

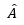
⇒ △ABH = △ACK (cạnh huyền – góc nhọn);

⇒ BH = CK (hai cạnh tương ứng).

b) Theo phần a) AH = AK;

Xét △AHI và △AKI vuông tại H và K có:

AI chung;

AH = AK (cmt);

⇒ △AHI = △AKI (hai cạnh góc vuông);

⇒

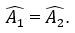
⇒ AI là tia phân giác của góc A (đpcm);

c) Gọi giao điểm của AI và KH là D. Ta phải chứng minh: D là trung điểm của HK hay D ≡ M.

Xét △AKD và △AHD có

AD chung;

(cmt);

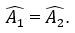
AK = AH (cmt);

⇒ △AKD = △AHD (c.g.c)

⇒ KD = HD (hai cạnh tương ứng);

Lại có D nằm giữa K và H (theo cách vẽ), nên D là trung điểm của HK.

⇒ D ≡ M (A, M, I thẳng hàng).

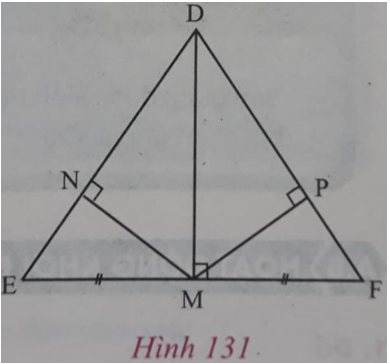
Câu 3: (trang 145 toán 7 VNEN tập 1). Tìm các cặp tam giác bằng nhau có trên hình 131.

Lời giải:

Từ hình 131, ta có:

+ △EDM = △FDM (hai cạnh góc vuông);

+ △EMN = △FMP (cạnh huyền – góc nhọn);

+ △DMN = △DMP (cạnh góc vuông – góc nhọn kề cạnh đó);

D.E. Hoạt động vận dụng & Tìm tòi mở rộng

Câu 1: (trang 145 toán 7 VNEN tập 1). Cho tam giác ABC. Các tia phân giác góc B và C cắt nhau tại O. Chứng minh AO là tia phân giác góc A.

Hướng dẫn: Từ O kẻ các đường vuông góc với các cạnh của tam giác ABC.

Lời giải:

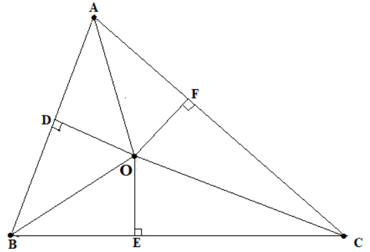
Từ O kẻ các đường OD, OE, OF lần lượt vuông góc với các cạnh AB, BC, CA. (hình vẽ)

Xét △BDO và △BEO vuông tại D và E có:

BO chung;

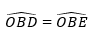
(BI là tia phân giác góc B);

⇒ △BDO = △BEO; (cạnh huyền – góc nhọn).

Suy ra: OD = OE (hai cạnh tương ứng). (1)

Chứng minh tương tự: △OEC = △OFC

Suy ra: OE = OF (hai cạnh tương ứng); (2)

Từ (1) và (2): OD = OE = OF.

Xét △ADO và △AFO vuông tại D và F có:

AO chung;

DO = FO (cmt);

⇒ △ADO = △AFO; (cạnh huyền – cạnh góc vuông).

⇒ (hai góc tương ứng);

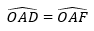
Suy ra: AO là tia phân giác góc A.

Câu 2: (trang 145 toán 7 VNEN tập 1). Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường trung trực của BC tại I. Kẻ IE vuông góc với đường thẳng AB, kẻ IF vuông góc với đường thẳng AC. Chứng minh BE = CF.

Lời giải:

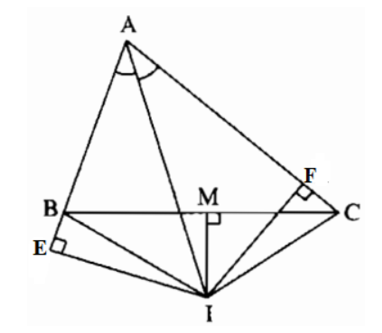
Xét △AEI và △AFI vuông tại E và F có:

AI chung;

(AI là tia phân giác góc B);

⇒ △AEI=△AFI; (cạnh huyền – góc nhọn).

Suy ra: IE = IF (hai cạnh tương ứng). (1)

Gọi M là trung điểm của BC.

Xét △BMI và △CMI vuông tại M có:

MI chung;

BM = CM;

⇒ △BMI=△CMI (hai cạnh góc vuông);

Suy ra: BI = CI (hai cạnh tương ứng). (2)

Xét △BEI và △CFI vuông tại E và F có:

IE = IF (từ (1));

BI = CI (từ (2));

⇒ △BEI =△CFI (cạnh huyền – cạnh góc vuông);

Suy ra: BE = CF (đpcm).

Câu 3: (trang 146 toán 7 VNEN tập 1). Đố: Em hãy thảo luận với các bạn và tìm hiểu trên Internet: Muốn đo khoảng cách giữa hai vật mà không thể đến trực tiếp được (hai vật cần đo khoảng cách nằm ở hai địa điểm cách xa nhau) thì có thể dùng tính chất của hai tam giác bằng nhau và các dụng cụ đo trong kĩ thuật, trong xây dựng để đo được không?

Lời giải:

Trong thực tế và trong kĩ thuật, muốn đo khoảng cách giữa hai vật mà ở cách xa nhau, ta có thể dùng kiến thức về hai tam giác bằng nhau và các dụng cụ đo trong kĩ thuật, xây dựng để đo.

Xem thêm các bài Giải bài tập Toán lớp 7 chương trình VNEN hay khác:

• Bài 5: Tam giác cân - Tam giác đều
• Bài 6: Định lý Py-ta-go
• Bài 7: Luyện tập
• Bài 9: Thực hành ngoài trời về tam giác,tam giác bằng nhau
• Bài 10: Ôn tập chương 2

Đã có lời giải bài tập lớp 7 sách mới:

• (mới) Giải bài tập Lớp 7 Kết nối tri thức
• (mới) Giải bài tập Lớp 7 Chân trời sáng tạo
• (mới) Giải bài tập Lớp 7 Cánh diều

Săn shopee siêu SALE :

• Sổ lò xo Art of Nature Thiên Long màu xinh xỉu
• Biti's ra mẫu mới xinh lắm
• Tsubaki 199k/3 chai
• L'Oreal mua 1 tặng 3

---