Tổng hợp lý thuyết Toán 12 Chương 1 Cánh diều
Tổng hợp lý thuyết Toán 12 Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số sách Cánh diều hay nhất, chi tiết với bài tập có lời giải sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm Toán 12 Chương 1.
Tổng hợp lý thuyết Toán 12 Chương 1 Cánh diều
(199k) Xem Khóa học Toán 12 CD
Tổng hợp lý thuyết Toán 12 Chương 1
1. Tính đơn điệu của hàm số
* Tính đơn điệu và dấu của đạo hàm
Cho hàm số y = f(x) có đạo hàm trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng.
- Nếu f'(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
- Nếu f'(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
Chú ý: Nếu hàm số y = f(x) đồng biến trên tập K hoặc nghịch biến trên tập K thì hàm số y = f(x) còn được gọi là đơn điệu trên K ⊂ ℝ.
- Cho hàm số y = f(x) có đạo hàm trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu f'(x) ≥ 0 (hoặc f'(x) ≤ 0) với mọi x thuộc K và f'(x) = 0 chỉ tại một số hữu hạn điểm của K thì hàm số f(x) đồng biến (hoặc nghịch biến) trên K.
* Các bước xét tính đồng biến, nghịch biến của hàm số y = f(x)
Bước 1. Tìm tập xác định của hàm số y = f(x).
Bước 2. Tính đạo hàm f'(x). Tìm các điểm xi (i = 1, 2, …, n) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
2. Điểm cực trị, giá trị cực trị của hàm số
* Định nghĩa
Cho hàm sốy = f(x) liên tục trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng và x0 ∈ K, x1 ∈ K.
+) x0 được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a; b) chứa điểm x0 sao cho (a; b) ⊂ K và f(x) < f(x0) với mọi x ∈ (a; b) và x ≠ x0.
Khi đó, f(x0) được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là fCĐ.
+) x1 được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (c; d) chứa điểm x1 sao cho (c; d) ⊂ K và f(x) > f(x1) với mọi x ∈ (c; d) và x ≠ x1.
Khi đó, f(x1) được gọi là giá trị cực tiểu của hàm số đã cho, kí hiệu là fCT.
+) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị).
Chú ý: Nếu x0 là một điểm cực trị của hàm số y = f(x) thì người ta nói rằng hàm số y = f(x) đạt cực trị tại điểm x0. Khi đó, điểm M(x0; f(x0)) được gọi là điểm cực trị của đồ thị hàm số y = f(x).
* Mối liên hệ giữa đạo hàm và cực trị
Giả sử hàm số y = f(x) liên tục trên khoảng (a; b) chứa điểm x0 và có đạo hàm trên các khoảng (a; x0) và (x0; b). Khi đó
+) Nếu f'(x) < 0 với mọi x ∈ (a; x0) và f'(x) > 0 với mọi x ∈ (x0; b) thì hàm số f(x) đạt cực tiểu tại điểm x0.
+) Nếu f'(x) > 0 với mọi x ∈ (a; x0) và f'(x) < 0 với mọi x ∈ (x0; b) thì hàm số f(x) đạt cực đại tại điểm x0.
* Các bước tìm điểm cực trị của hàm số f(x)
Bước 1. Tìm tập xác định của hàm số f(x):
Bước 2. Tính đạo hàm f'(x). Tìm các điểm xi (i = 1, 2, …, n) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các điểm cực trị của hàm số.
3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3.1. Định nghĩa
Cho hàm số y = f(x) xác định trên tập D.
+) Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D, kí hiệu M = , nếu f(x) ≤ M với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = M.
+) Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D, kí hiệu m = , nếu f(x) ≥ m với mọi x ∈ D và tồn tại x1 ∈ D sao cho f(x1) = m.
Chú ý: Khi tìm giá trị lớn nhất (hoặc giá trị nhỏ nhất) của hàm số mà không chỉ rõ tập D thì ta tìm giá trị lớn nhất (hoặc giá trị nhỏ nhất) của hàm số đó trên cả tập xác định của nó.
3.2. Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số bằng đạo hàm
- Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) trên một khoảng, đoạn hay nửa khoảng, ta có thể lập bảng biến thiên của hàm số trên tập hợp đó. Căn cứ vào bảng biến thiên, ta tìm được giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
- Nhận xét: Người ta chứng minh được rằng: Mọi hàm số liên tục trên một đoạn đều có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn đó.
Giả sử hàm số f(x) liên tục trên đoạn [a; b] và có đạo hàm trên khoảng (a; b), có thể trừ một số hữu hạn điểm. Nếu f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc khoảng (a; b) thì ta có quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b] như sau:
Bước 1. Tìm các điểm x1, x2, …, xn thuộc khoảng (a; b) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 2. Tính f(x1), f(x2), …, f(xn), f(a) và f(b).
Bước 3. So sánh các giá trị tìm được ở Bước 2.
Số lớn nhất trong các giá trị đó là giá trị lớn nhất của hàm số f(x) trên đoạn [a; b], số nhỏ nhất trong các giá trị đó là giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b].
4. Đường tiệm cận của đồ thị hàm số
4.1. Đường tiệm cận ngang
Đường thẳng y = y0 được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu: hoặc
Nhận xét: Giả sử đường thẳng y = y0 là tiệm cận ngang của đồ thị hàm số y = f(x). Lấy điểm M(x; y) thuộc đồ thị hàm số. Gọi MH là khoảng cách từ điểm M đến đường thẳng y = y0. Khi đó, độ dài MH tiến tới 0 khi x → + ∞ hay x → – ∞.
4.2. Đường tiệm cận đứng
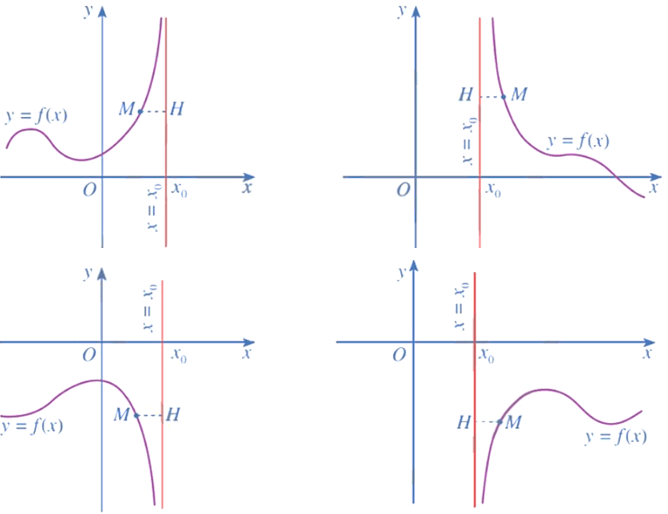
Đường thẳng x = x0 được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Nhận xét: Giả sử đường thẳng x = x0 là tiệm cận đứng của đồ thị hàm số y = f(x). Lấy điểm M(x; y) thuộc đồ thị hàm số. Gọi MH là khoảng cách từ điểm M đến đường thẳng x = x0. Khi đó, độ dài MH tiến tới 0 khi x → x0+ hay x → x0–.
4.3. Đường tiệm cận xiên
Đường thẳng y = ax + b (a ≠ 0) được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu:
hoặc
Nhận xét: Giả sử đường thẳng y = ax + b (a ≠ 0) là tiệm cận xiên của đồ thị hàm số y = f(x). Lấy điểm M thuộc đồ thị hàm số y = f(x) và điểm N thuộc đường thẳng y = ax + b có cùng hoành độ x. Khi đó, độ dài MN tiến tới 0 khi x → + ∞ hay x → – ∞.
Chú ý: Để xác định hệ số a, b của đường tiệm cận xiên y = ax + b của đồ thị hàm số y = f(x), ta có thể áp dụng công thức sau:
và hoặc và
(Khi a = 0 thì ta có tiệm cận ngang y = b).
5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
5.1. Sơ đồ khảo sát hàm số
Để khảo sát và vẽ đồ thị hàm số, ta có thể thực hiện các bước sau:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số
- Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận (nếu có).
- Tính đạo hàm y' và tìm các điểm mà tại đó đạo hàm bằng 0.
- Lập bảng biến thiên; xác định chiều biến thiên, cực trị của hàm số (nếu có).
Bước 3. Vẽ đồ thị hàm số
- Vẽ các đường tiệm cận (nếu có).
- Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục tọa độ (trong trường hợp đơn giản), …
- Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
Chú ý: Đồ thị hàm số y = f(x) giao với trục hoành tại những điểm có hoành độ là nghiệm của phương trình f(x) = 0, giao với trục tung tại điểm có tung độ là f(0) nếu 0 thuộc tập xác định của hàm số đó.
5.2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba
Sử dụng sơ đồ khảo sát hàm số, ta có thể khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba.
Nhận xét: Trong trường hợp tổng quát, đồ thị hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) có tâm đối xứng là điểm Hoành độ của tâm đối xứng đó là nghiệm của phương trình y" = 0.
5.3. Khảo sát sự biến thiên và vẽ đồ thị của hàm số phân thức hữu tỉ
5.3.1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
(c ≠ 0, ad – bc ≠ 0)
Sử dụng sơ đồ khảo sát hàm số, ta có thể khảo sát sự biến thiên và vẽ đồ thị của hàm số y = (c ≠ 0, ad – bc ≠ 0).
Nhận xét: Trong trường hợp tổng quát, đồ thị của hàm số y = (c ≠ 0, ad – bc ≠ 0) nhận giao điểm của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
5.3.2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
y = (a ≠ 0, m ≠ 0)
Sử dụng sơ đồ khảo sát hàm số, ta có thể khảo sát sự biến thiên và vẽ đồ thị của hàm số (a ≠ 0, m ≠ 0, không là nghiệm của đa thức ax2 + bx + c).
Nhận xét: Trong trường hợp tổng quát, đồ thị của hàm số y = (a ≠ 0, m ≠ 0, không là nghiệm của đa thức ax2 + bx + c) nhận giao điểm I của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
5.4. Ứng dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Đạo hàm là một khái niệm toán học xuất phát từ nhiều vấn đề trong khoa học, kĩ thuật và công nghệ. Vì thế đạo hàm và khảo sát hàm số là một công cụ quan trọng để giải quyết một số bài toán trong thực tiễn.
Bài tập ôn tập Chương 1
1. Bài tập trắc nghiệm
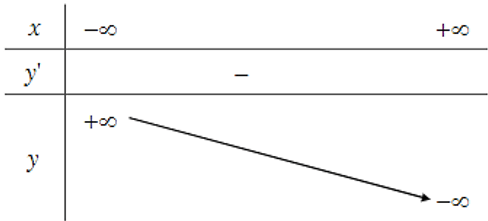
Bài 1. Cho hàm số y = f(x) có bảng biến thiên như sau:
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A. (– ∞; 0).
B. (0; 2).
C. (– 2; 0).
D. (2; + ∞).
Hướng dẫn giải
Đáp án đúng là: B
Dựa vào bảng biến thiên, ta thấy y' > 0 với mọi x ∈ (0; 2) nên hàm số đồng biến trên khoảng (0; 2).
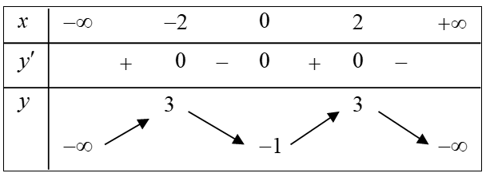
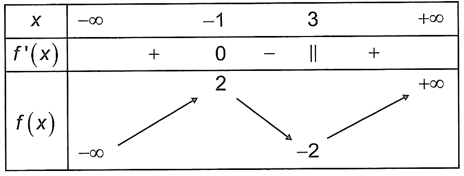
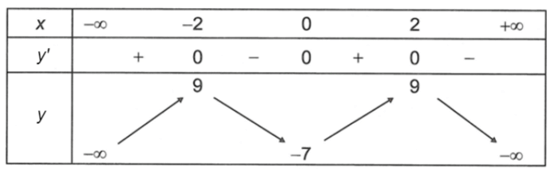
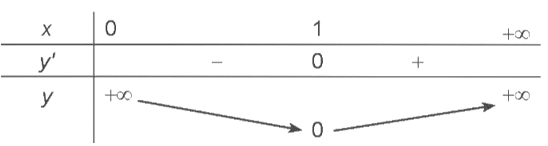
Bài 2. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây
Mệnh đề nào sau đây sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có hai cực trị.
C. Cực đại bằng – 1.
D. Cực tiểu bằng – 2.
Hướng dẫn giải
Đáp án đúng là: C
Từ bảng biến thiên, ta thấy hàm số y = f(x) có đạt cực tiểu tại điểm x = 3, yCT = – 2; đạt cực đại tại điểm x = – 1, yCĐ = 2.
Vậy các đáp án A, B, D đúng và đáp án C sai.
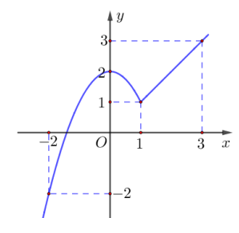
Bài 3. Cho hàm số y = f(x), x ∈ [– 2; 3] có đồ thị như hình vẽ dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [– 2; 3].
Giá trị S = M + m là
A. 3.
B. 1.
C. 6.
D. 5.
Hướng dẫn giải
Đáp án đúng là: B
Từ đồ thị, ta có M = 3 và m = – 2. Suy ra, S = M + m = 3 + (– 2) = 1.
Bài 4. Giá trị lớn nhất của hàm số f(x) = (x – 3)2 ∙ ex trên đoạn [2; 4] là
A. 0.
B. e2.
C. e3.
D. e4.
Hướng dẫn giải
Đáp án đúng là: D
Ta có f'(x) = 2(x – 3) ∙ ex + (x – 3)2 ∙ ex = (x – 3) ∙ ex ∙ (x – 1).
Khi đó, trên khoảng (2; 4), f'(x) = 0 khi x = 3.
f(2) = e2; f(3) = 0; f(4) = e4.
Vậy tại x = 4.
Bài 5. Tiệm cận ngang của đồ thị hàm số là
A. x = 3.
B. y = 3.
C. x = – 2.
D. y = – 2.
Hướng dẫn giải
Đáp án đúng là: B
Hàm số đã cho có tập xác định là ℝ \ {– 2}.
Ta có:
Vậy đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số đã cho.
Bài 6. Tiệm cận xiên của đồ thị hàm số là
A. y = x – 1.
B. y = x + 3.
C. y = x – 3.
D. y = x.
Hướng dẫn giải
Đáp án đúng là: C
Do nên đường thẳng y = x – 3 là tiệm cận xiên của đồ thị hàm số đã cho.
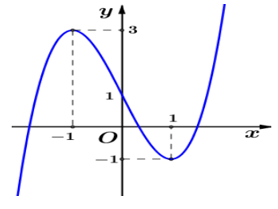
Bài 7. Đường cong trong hình vẽ dưới đây là đồ thị của hàm số:
A. y = x3 – 3x + 1.
B. y = x3 – 3x2 + 1.
C. y = – x3 + 3x + 1.
D. y = – x3 – 3x2 – 1.
Hướng dẫn giải
Đáp án đúng là: A
Quan sát hình vẽ ta thấy đồ thị hàm số trên có hai điểm cực trị là (– 1; 3) và (1; – 1) và đồ thị hàm số đi qua điểm (0; 1).
Xét hàm số y = x3 – 3x + 1:
+ Có y' = 3x2 – 3; y' = 0 ⇔ x = – 1 hoặc x = 1.
Với x = – 1 thì y = 3 và với x = 1 thì y = – 1.
Từ đó suy ra hai điểm cực trị của đồ thị hàm số là (– 1; 3) và (1; – 1).
+ Với x = 0 thì y = 1, suy ra đồ thị hàm số cắt trục tung tại điểm (0; 1).
Vậy đường cong trong hình vẽ trên là đồ thị của hàm số y = x3 – 3x + 1.
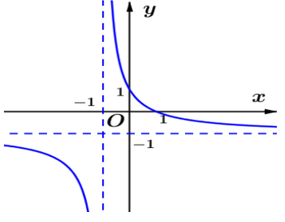
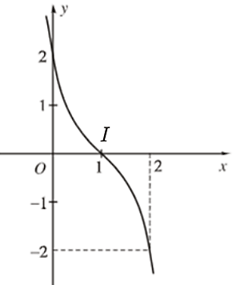
Bài 8. Đường cong trong hình vẽ dưới đây là đồ thị của hàm số:
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: B
+ Đồ thị hàm số có đường tiệm cận ngang là y = – 1 nên loại các đáp án C và D.
+ Đồ thị hàm số đi qua điểm (0; 1) nên loại đáp án A.
2. Bài tập tự luận
Bài 1. Tìm các khoảng đơn điệu của mỗi hàm số sau:
a) y = x3 + 3x2 – 9x + 15;
b) y = – x4 + 2x2 – 4;
c) y = ;
d) y =
Hướng dẫn giải
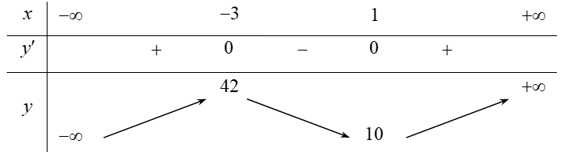
a) y = x3 + 3x2 – 9x + 15
Hàm số đã cho có tập xác định là ℝ.
Ta có y' = 3x2 + 6x – 9;
y' = 0 ⇔ 3x2 + 6x – 9 = 0 ⇔ x = – 3 hoặc x = 1.
Bảng biến thiên của hàm số như sau:
Vậy hàm số đồng biến trên mỗi khoảng (– ∞; – 3) và (1; + ∞); nghịch biến trên mỗi khoảng (– 3; 1).
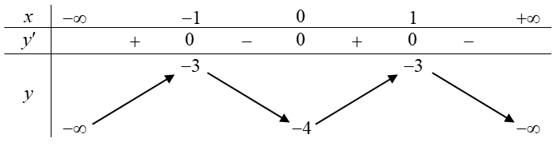
b) y = – x4 + 2x2 – 4
Hàm số đã cho có tập xác định là ℝ.
Ta có y' = – 4x3 + 4x;
y' = 0 ⇔– 4x3 + 4x = 0 ⇔ x = – 1 hoặc x = 0 hoặc x = 1.
Bảng biến thiên của hàm số như sau:
Vậy hàm số đồng biến trên mỗi khoảng (– ∞; – 1) và (0; 1); nghịch biến trên mỗi khoảng (– 1; 0) và (1; + ∞).
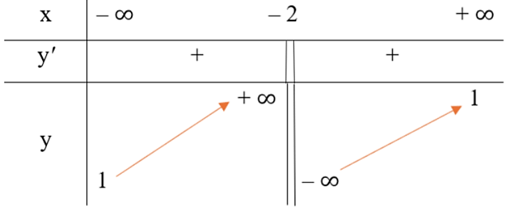
c) y =
Hàm số đã cho có tập xác định là ℝ \ {– 2}.
Ta có y' = ; y' > 0 với mọi x ≠ – 2.
Bảng biến thiên của hàm số như sau:
Vậy hàm số đồng biến trên mỗi khoảng (– ∞; – 2) và (– 2; + ∞).
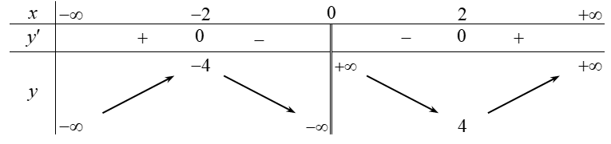
d) y =
Hàm số đã cho có tập xác định là ℝ \ {0}.
Ta có y' =
y' = 0 ⇔ = 0 ⇔ x = – 2 hoặc x = 2.
Bảng biến thiên của hàm số như sau:
Vậy hàm số đồng biến trên mỗi khoảng (– ∞; – 2) và (2; + ∞); nghịch biến trên mỗi khoảng (– 2; 0) và (0; 2).
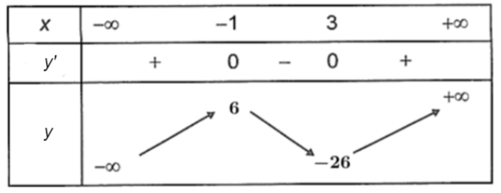
Bài 2. Tìm điểm cực trị của mỗi hàm số sau:
a) y = x3 – 3x2 – 9x + 1;
b) y = – x4 + 8x2 – 7;
c) y =
Hướng dẫn giải
a) y = x3 – 3x2 – 9x + 1
Hàm số đã cho có tập xác định là ℝ.
Ta có y' = 3x2 – 6x – 9;
y' = 0 ⇔3x2 – 6x – 9 = 0 ⇔ x = – 1 hoặc x = 3.
Bảng biến thiên của hàm số như sau:
Vậy hàm số đạt cực đại tại điểm x = – 1; đạt cực tiểu tại điểm x = 3.
b) y = – x4 + 8x2 – 7
Hàm số đã cho có tập xác định là ℝ.
Ta có y' = – 4x3 + 16x;
y' = 0 ⇔– 4x3 + 16x = 0 ⇔ x = – 2 hoặc x = 0 hoặc x = 2.
Bảng biến thiên của hàm số như sau:
Vậy hàm số đạt cực đại tại điểm x = – 2 và x = 2; đạt cực tiểu tại điểm x = 0.
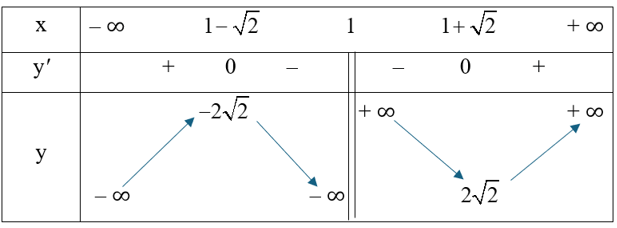
c) y =
Hàm số đã cho có tập xác định là ℝ\{1}.
Ta có y' =
y' = 0 ⇔ = 0 hoặc
Bảng biến thiên của hàm số như sau:
Vậy hàm số đạt cực đại tại điểm ; đạt cực tiểu tại .
Bài 3. Một vật được phóng thẳng đứng lên trên từ độ cao 3 m với vận tốc ban đầu là 39,2 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức
h(t) = 3 + 39,2t – 4,9t2.
Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Hướng dẫn giải
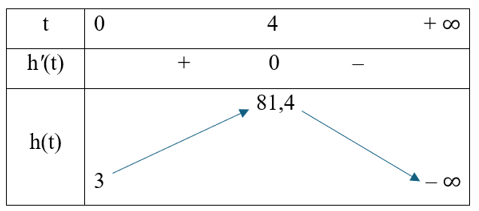
Xét hàm số h(t) = 3 + 39,2t – 4,9t2.
Tập xác định của hàm số là [0; + ∞).
Ta có h'(t) = 39,2 − 9,8t;
h'(t) = 0 t = 4.
Bảng biến thiên của hàm số như sau:
Căn cứ vào bảng biến thiên ta có hàm số h(t) đạt cực đại tại t = 4, h(t)CĐ = 81,4.
Vậy tại thời điểm t = 4 thì vật đạt độ cao lớn nhất là 81,4 m.
Bài 4. Tìm giá trị nhỏ nhất của hàm số y = x – 2 + trên khoảng (0; + ∞).
Hướng dẫn giải
Xét hàm số với x ∈ (0; + ∞).
Ta có y' = 1. Khi đó, trên khoảng (0; + ∞), y' = 0 khi x = 1.
Ngoài ra,
Bảng biến thiên của hàm số như sau:
Căn cứ vào bảng biến thiên, ta có tại x = 1.
Bài 5. Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:
a) f(x) = x3 – 3x + 5 trên đoạn [0; 2];
b) f(x) = x – sin 2x trên đoạn [0; π].
Hướng dẫn giải
a) Ta có f'(x) = 3x2 – 3. Khi đó trên khoảng (0; 2), f'(x) = 0 khi x = 1.
f(0) = 5; f(1) = 3; f(2) = 7.
Vậy tại x = 2; tại x = 1.
b) Ta có f'(x) = 1 – 2cos 2x.
Khi đó trên khoảng (0; π), f'(x) = 0 khi x = hoặc x =
f(0) = 0;
Vậy tại x = ; tại x = .
Bài 6. Khi xây nhà, chủ nhà cần làm một bồn nước bằng gạch và xi măng có dạng hình hộp đứng đáy là hình chữ nhật có chiều rộng là x (m), chiều dài gấp 2 lần chiều rộng và không nắp, có chiều cao là h (m), có thể tích là m3. Tìm chiều rộng của đáy hình chữ nhật để chi phí xây dựng là thấp nhất.
Hướng dẫn giải
Chiều dài hình chữ nhật là 2x (m).
Ta có
Diện tích xung quanh của bồn nước (không nắp) là
S = 2(xh + 2xh) + 2x2 = 6xh + 2x2 = + 2x2 (m2) với x > 0.
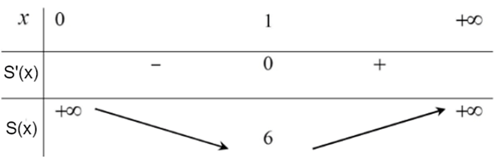
Xét hàm số S(x) = + 2x2 với x ∈ (0; + ∞).
Ta có S'(x) =; S'(x) = 0 ⇔ x = 1 ∈ (0; + ∞).
Bảng biến thiên của hàm số như sau:
Căn cứ vào bảng biến thiên, ta có tại x = 1.
Để chi phí xây dựng là thấp nhất thì diện tích xung quanh của bồn nước phải nhỏ nhất.
Vậy chiều rộng của đáy hình chữ nhật bằng 1 m thì chi phí xây dựng là thấp nhất.
Bài 7. Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của mỗi đồ thị hàm số sau:
a)
b)
c) y = 2x – 1 +
Hướng dẫn giải
a)
Hàm số đã cho có tập xác định là ℝ \ {– 1}.
Ta có
Do đó, đường thẳng y = – 1 là tiệm cận ngang của đồ thị hàm số đã cho.
Lại có
Do đó, đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số đã cho.
Đồ thị hàm số đã cho không có tiệm cận xiên.
b)
Hàm số đã cho có tập xác định là ℝ \ {– 1}.
Ta có
Do đó, đồ thị hàm số đã cho không có tiệm cận ngang.
Lại có
Do đó, đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số đã cho.
Ta có
;
Do đó, đường thẳng y = x – 4 là tiệm cận xiên của đồ thị hàm số đã cho.
c) y = 2x – 1 +
Hàm số đã cho có tập xác định là ℝ \ {0}.
Đồ thị hàm số đã cho không có tiệm cận ngang.
Ta có
Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số đã cho.
Lại có
Do đó, đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho.
Bài 8. Nếu trong một ngày, một xưởng sản xuất được x sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức:
a) Tìm các đường tiệm cận của đồ thị hàm số y = C(x).
b) Nêu nhận xét về chi phí của một sản phẩm khi số sản phẩm được sản xuất trong một ngày x đủ lớn.
Hướng dẫn giải
a) Xét hàm số với x ∈ (0; + ∞).
Ta có: Do đó, đường thẳng y = 50 là tiệm cận ngang của đồ thị hàm số y = C(x).
Lại có Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số y = C(x).
b) Khi x → + ∞, ta có C(x) → 50, điều đó có nghĩa là khi x đủ lớn thì chi phí sản xuất một sản phẩm sẽ gần bằng 50 nghìn đồng.
Bài 9. Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) y = – x3 + 3x2 – 4x + 2;
b)
c)
Hướng dẫn giải
a) y = – x3 + 3x2 – 4x + 2
1) Tập xác định: ℝ.
2) Sự biến thiên
- Giới hạn tại vô cực:
- y' = – 3x2 + 6x – 4 = – 3(x – 1)2 – 1 < 0 với mọi x ∈ ℝ;
- Bảng biến thiên:
Hàm số nghịch biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; 2).
- Giao điểm của đồ thị với trục hoành:
Xét phương trình – x3 + 3x2 – 4x + 2 = 0 ⇔ (x – 1)( – x2 + 2x – 2) = 0 ⇔ x = 1.
Vậy đồ thị hàm số giao với trục hoành tại điểm (1; 0).
Đồ thị hàm số đã cho được biểu diễn như hình dưới đây.
Đồ thị của hàm số có tâm đối xứng là điểm I(1; 0).
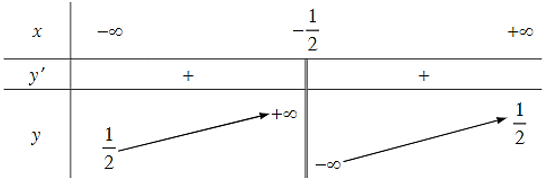
b)
1) Tập xác định: ℝ \
2) Sự biến thiên
- Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
Do đó, đường thẳng x = là tiệm cận đứng của đồ thị hàm số.
Do đó, đường thẳng y = là tiệm cận ngang của đồ thị hàm số.
> 0 với mọi x ≠ .
- Bảng biến thiên:
Hàm số đồng biến trên mỗi khoảng và
Hàn số không có cực trị.
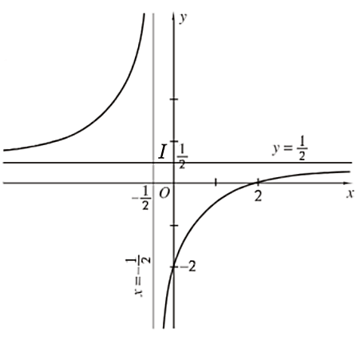
3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; – 2).
- Giao điểm của đồ thị với trục hoành: (2; 0).
Đồ thị hàm số đã cho được vẽ như hình dưới đây.
Đồ thị hàm số nhận giao điểm I của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng.
c)
1) Tập xác định: ℝ \ {2}.
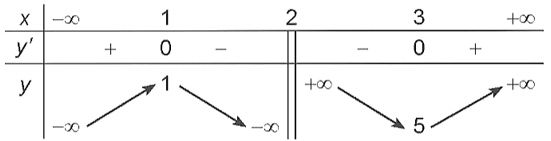
2) Sự biến thiên
- Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng:
. Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
. Do đó, đường thẳng y = x + 1 là tiệm cận xiên của đồ thị hàm số.
y' = 0 ⇔ x = 1 hoặc x = 3.
- Bảng biến thiên:
Hàm số đồng biến trên mỗi khoảng (– ∞; 1) và (3; + ∞); nghịch biến trên mỗi khoảng (1; 2) và (2; 3).
Hàm số đạt cực đại tại x = 1, yCĐ = 1; đạt cực tiểu tại x = 3, yCT = 5.
3) Đồ thị
- Giao điểm của đồ thị với trục tung:
- Giao điểm của đồ thị với trục hoành:
Ta có y = 0 ⇔ x2 – x – 1 = 0
⇔ x = hoặc x =
Vậy đồ thị hàm số giao với trục Ox tại điểm và điểm
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
Đồ thị hàm số nhận giao điểm I(2; 3) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Bài 10. Một nhà sản xuất làm những hộp đựng hình trụ có thể tích 1 lít. Tìm các kích thước của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất (kết quả được tính theo centimét và làm tròn đến chữ số thập phân thứ hai).
Hướng dẫn giải
Đổi 1 lít = 1 000 cm3.
Gọi r (cm) là bán kính đáy của hình trụ, h (cm) là chiều cao của hình trụ.
Diện tích toàn phần của hình trụ là S = 2πr2 + 2πh.
Do thể tích của hình trụ là 1 000 cm3 nên ta có: 1000 = V = πr2h, hay
Do đó, diện tích toàn phần của hình trụ là S = 2πr2 + , r > 0.
Ta cần tìm r sao cho S đạt giá trị nhỏ nhất.
Ta có:
S' = 0 ⇔ πr3 = 500 ⇔ r =
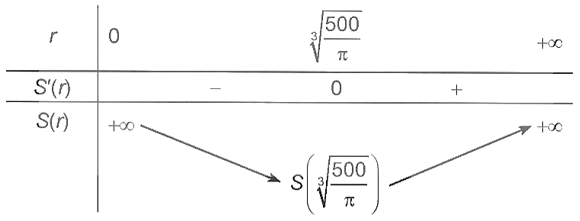
Bảng biến thiên:
Khi đó,
Vậy cần sản xuất các hộp đựng hình trụ có bán kính đáy (cm) và chiều cao (cm).
Học tốt Chương 1
Các bài học để học tốt Bài tập cuối chương 1 Toán lớp 12 hay khác:
(199k) Xem Khóa học Toán 12 CD
Xem thêm tóm tắt lý thuyết Toán lớp 12 Cánh diều hay khác:
Lý thuyết Toán 12 Bài 1: Vectơ và các phép toán vectơ trong không gian
Lý thuyết Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ
Lý thuyết Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm
Xem thêm các tài liệu học tốt lớp 12 hay khác:
- Giải sgk Toán 12 Cánh diều
- Giải Chuyên đề học tập Toán 12 Cánh diều
- Giải SBT Toán 12 Cánh diều
- Giải lớp 12 Cánh diều (các môn học)
- Giải lớp 12 Kết nối tri thức (các môn học)
- Giải lớp 12 Chân trời sáng tạo (các môn học)
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

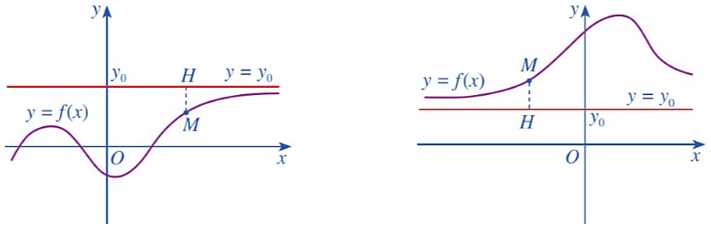
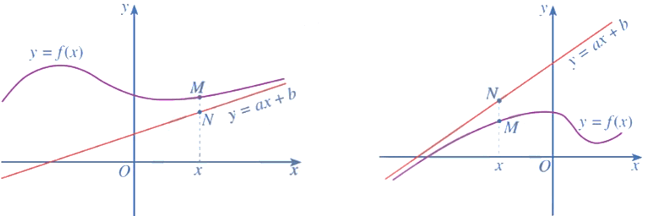
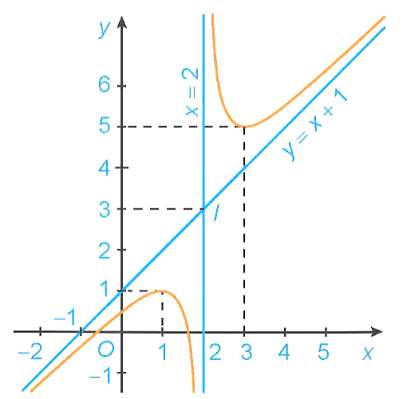



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

