Tổng hợp lý thuyết Toán 12 Chương 3 Cánh diều

Tổng hợp lý thuyết Toán 12 Chương 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm sách Cánh diều hay nhất, chi tiết với bài tập có lời giải sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm Toán 12 Chương 3.

Tổng hợp lý thuyết Toán 12 Chương 3 Cánh diều

Lý thuyết tổng hợp Chương 3

1. Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

1.1. Khoảng biến thiên

● Định nghĩa

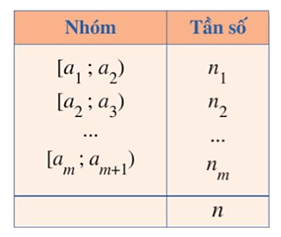
Xét mẫu số liệu ghép nhóm cho bởi bảng sau, trong đó n₁ > 0 và n_m > 0.

Gọi a₁, a_{m + 1} lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm m.

Hiệu R = a_{m + 1} – a₁ được gọi là khoảng biến thiên của mẫu số liệu ghép nhóm đó.

Chú ý: Đối với mẫu số liệu ghép nhóm mà ta biết mẫu số liệu không ghép nhóm sinh ra nó thì ta cũng có thể chọn khoảng biến thiên của mẫu số liệu không ghép nhóm chính là khoảng biến thiên của mẫu số liệu ghép nhóm.

● Ý nghĩa

+ Khoảng biến thiên của mẫu số liệu ghép nhóm đo mức độ phân tán của mẫu số liệu đó. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

+ Trong các đại lượng đo mức độ phân tán của mẫu số liệu ghép nhóm, khoảng biến thiên là đại lượng dễ hiểu, dễ tính toán. Tuy nhiên, do khoảng biến thiên chỉ sử dụng hai giá trị a₁ và a_{m + 1} của mẫu số liệu nên đại lượng đó dễ bị ảnh hưởng bởi các giá trị bất thường.

+ Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc.

1.2. Khoảng tứ phân vị

● Xét mẫu số liệu ghép nhóm cho bởi bảng sau:

Gọi Q₁, Q₂, Q₃ là tứ phân vị của mẫu số liệu đó. Ta gọi hiệu ∆_Q = Q₃ – Q₁ là khoảng tứ phân vị của mẫu số liệu đó.

● Ý nghĩa:

+ Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.

+ Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị bất thường của mẫu đó. Khoảng tứ phân vị thường được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết giá trị bất thường của mẫu số liệu và nó không bị ảnh hưởng bởi các giá trị bất thường đó.

2. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm.

2.1. Định nghĩa

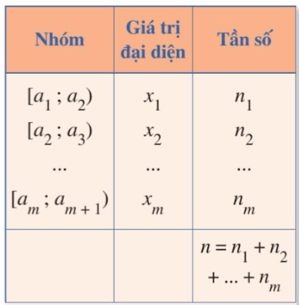
Xét mẫu số liệu ghép nhóm cho bởi bảng sau:

Gọi $\overline{x}$ là số trung bình cộng của mẫu số liệu đó.

Số s² = $\frac{n_1{\left(x_1-\overline{x}\right)}^2+n_2{\left(x_2-\overline{x}\right)}^2+\mathrm{....}+n_m{\left(x_m-\overline{x}\right)}^2}{n}$  được gọi là phương sai của mẫu số liệu đó.

Căn bậc hai (số học) của phương sai gọi là độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, nghĩa là s = $\sqrt{s^2}$.

2.2. Ý nghĩa

● Phương sai (độ lệch chuẩn) của mẫu số liệu ghép nhóm xấp xỉ phương sai (độ lệch chuẩn) của mẫu số liệu gốc và được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm đó.

● Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.

● Khi hai mẫu số liệu ghép nhóm có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn.

Bài tập ôn tập Chương 3

1. Bài tập trắc nghiệm

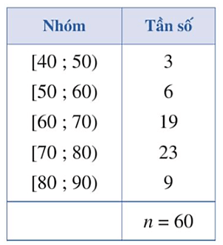
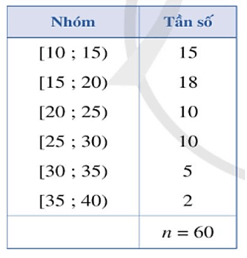
Bài 1. Bảng dưới đây biểu diễn số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

A. 50.

B. 30.

C. 6.

D. 69,8.

b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần với giá trị nào dưới đây?

A. 50.

B. 40.

C. 14,23.

D. 70,87.

Lời giải

a) Đáp án đúng là: A

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: R = 90 – 40 = 50 (nghìn đồng).

b) Đáp án đúng là: C

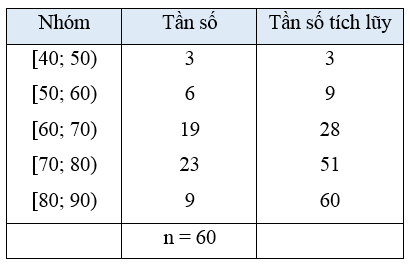
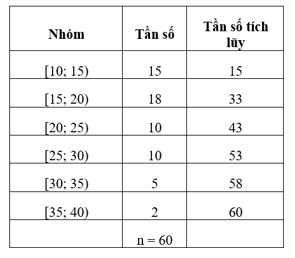
Từ bảng thống kê đã cho, ta có bảng tần số tích lũy như sau:

Ta có: $\frac{n}{4}=\frac{60}{4}=15$  mà 9 < 15 < 28.

Suy ra nhóm thứ ba là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15.

Xét nhóm thứ ba là nhóm [60; 70) có s = 60, h = 10, n₃ = 19 và nhóm 2 là nhóm

[50; 60) có tần số tích lũy cf₂ = 9. Ta có:

Q₁ = s + $\left(\frac{15-c{f}_2}{n_3}\right).h$ = 60 +$\frac{15-9}{19}.10$ = $\frac{1200}{19}$  (nghìn đồng).

Ta có: $\frac{3n}{4}=\frac{3.60}{4}=45$ mà 28 < 45 < 51.

Nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45.

Nhóm 4 có đầu mút trái t = 70, độ dài l = 10, tần số của nhóm là n₄ = 23 và nhóm 3 có tần số tích lũy cf₃ = 28. Ta có:

Q₃ = t + $\left(\frac{45-c{f}_3}{n_4}\right).l$  = 70 + $\left(\frac{45-28}{23}\right).10$  = $\frac{1780}{23}$  (nghìn đồng).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = $\frac{1780}{23}$  − $\frac{1200}{19}$  = $\frac{6220}{437}$  ≈ 14,23 (nghìn đồng).

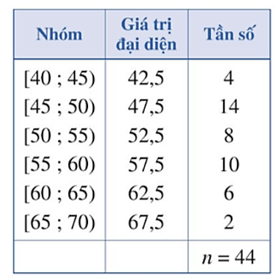
Bài 2. Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong vòng một ngày. Số liệu được ghi lại trong dưới đây.

a) Phương sai của mẫu số liệu ghép nhóm trên gần với giá trị nào sau đây?

A. 53,2.

B. 46,1.

C. 30.

D. 11.

b) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười) là:

A. 6,8.

B. 7,3.

C. 3,3.

D. 46,1.

Lời giải

a) Đáp án đúng là: B

Số trung bình cộng của mẫu số liệu ghép nhóm trên là:

$\overline{x}$ = $\frac{4.42,5+14.47,5+8.52,5+10.57,5+6.62,5+2.67,5}{44}$  = $\frac{585}{11}$ ≈ 53,18.

Phương sai của mẫu số liệu trên là:

s² = $\frac{1}{44}$ .[4 . (42,5 – 53,18)² + 14 . (47,5 – 53,18)² + 8 . (52,5 – 53,18)²

           + 10 . (57,5 – 53,18)² + 6 . (62,5 – 53,18)² + 2 . (67,5 – 53,18)²] ≈ 46,1.

b) Đáp án đúng là: A

Độ lệch chuẩn của mẫu số liệu trên là: s = $\sqrt{46,1}$  ≈ 6,8.

2. Bài tập tự luận

Bài 1. Bảng dưới đây biểu diễn số liệu ghép nhóm thống kê mức lương của một số nhân viên của một công ty (đơn vị: triệu đồng).

a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.

b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.

Lời giải

a) Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a₁ = 10, đầu mút phải của nhóm 6 là a₇ = 40.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

R = a₇ – a₁ = 40 – 10 = 30 (triệu đồng).

b) Ta có bảng tần số tích lũy như sau:

Số phần tử của mẫu là n = 60.

Ta có: $\frac{n}{4}=\frac{60}{4}=15$ suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15.

Xét nhóm 1 là nhóm [10; 15) có s = 10, h = 5, n₁ = 15 và có cf₀ = 0.

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

Q₁ = s + $\left(\frac{15-c{f}_0}{n_1}\right).h$ = 10 + $\left(\frac{15-0}{15}\right).5$  = 15 (triệu đồng).

Ta có: $\frac{3n}{4}=\frac{3.60}{4}=45$ mà 43 < 45 < 53 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45.

Xét nhóm 4 là nhóm [25; 30) có t = 25, l = 5, n₄ = 10 và nhóm 3 là nhóm [20; 25) có cf₃ = 43.

Áp dụng công thức, ta có tứ phân vị thứ ba là:

Q₃ = t + $\left(\frac{45-c{f}_3}{n_4}\right).l$ = 25 + $\left(\frac{45-43}{10}\right).5$ = 26 (triệu đồng).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = 26 − 15 = 11 (triệu đồng).

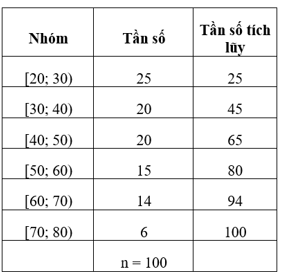
Bài 2. Bảng dưới đây biểu diễn số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.

a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.

b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.

Lời giải

a) Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a₁ = 20, đầu mút phải của nhóm 6 là a₇ = 80.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

R = a₇ – a₁ = 80 – 20 = 60 (tuổi).

b) Ta có bảng tần số tích lũy như sau:

Số phần tử của mẫu là n = 100.

Ta có: $\frac{n}{4}=\frac{100}{4}=25$ suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25.

Xét nhóm 1 là nhóm [20; 30) có s = 20, h = 10, n₁ = 25 và có cf₀ = 0.

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

Q₁ = s + $\left(\frac{25-c{f}_0}{n_1}\right).h$ = 20 + $\left(\frac{25-0}{25}\right).10$ = 30 (tuổi).

Ta có: $\frac{3n}{4}=\frac{3.100}{4}=75$ mà 65 < 75 < 80 nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75.

Xét nhóm 4 là nhóm [50; 60) có t = 50, l = 10, n₄ = 15 và nhóm 3 là nhóm [40; 50) có cf₃ = 65.

Áp dụng công thức, ta có tứ phân vị thứ ba là:

Q₃ = t + $\left(\frac{75-c{f}_3}{n_4}\right).l$ = 50 + $\left(\frac{75-65}{15}\right).10$ = $\frac{170}{3}$ (tuổi).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = $\frac{170}{3}$ − 30 = $\frac{80}{3}$ ≈ 26,67 (tuổi).

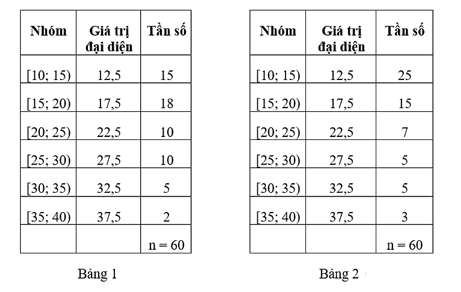
Bài 3. Bảng 1, Bảng 2 lần lượt biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của nhân viên của hai công ty A, B (đơn vị: triệu đồng).

a) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A, B.

b) Công ty nào có mức lương đồng điều hơn?

Lời giải

a) Số trung bình cộng của mẫu số liệu ghép nhóm cho bởi Bảng 1 là:

${\overline{x}}_1$ = $\frac{15.12,5+18.17,5+10.22,5+10.27,5+5.32,5+2.37,5}{60}$ = $\frac{62}{3}$ ≈ 20,67.

Ta có: 15. (12,5 – 20,67)² + 18. (17,5 − 20,67)² + 10. (22,5 − 20,67)²

       + 10. (27,5 – 20,67)² + 5. (32,5 – 20,67)² + 2. (37,5 – 20,67)² ≈ 2948,334.

Phương sai của mẫu số liệu ghép nhóm ở Bảng 1 là: $s_1^2$ = $\frac{2948,334}{60}$ ≈ 49,1389.

Độ lệch chuẩn của mẫu số liệu ghép nhóm ở Bảng 1 là:

s₁ ≈ $\sqrt{49,1389}$ ≈ 7 (triệu đồng).

 Số trung bình cộng của mẫu số liệu ghép nhóm cho bởi Bảng 2 là:

${\overline{x}}_2$= $\frac{25.12,5+15.17,5+7.22,5+5.27,5+5.32,5+3.37,5}{60}$ = $\frac{1145}{60}$ ≈ 19,08.

Ta có: 25. (12,5 – 19,08)² + 15. (17,5 – 19,08)² + 7. (22,5 – 19,08)²

       + 5. (27,5 – 19,08)² + 5. (32,5 – 19,08)² + 3. (37,5 – 19,08)² ≈ 3474,584.

Phương sai của mẫu số liệu ghép nhóm ở Bảng 2 là: $s_2^2$ =$\frac{3474,584}{60}$ ≈ 57,9097.

Độ lệch chuẩn của mẫu số liệu ghép nhóm ở Bảng 2 là:

s₂ ≈ $\sqrt{57,9097}$ ≈ 7,61 (triệu đồng).

b) Vì s₁ ≈ 7 < s₂ ≈ 7, 61 nên mức lương ở công ty A đồng đều hơn công ty B.

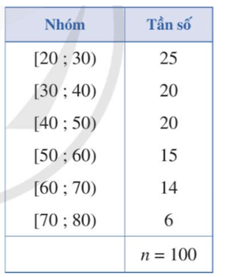
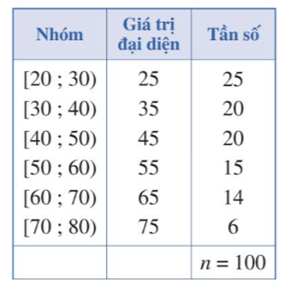
Bài 4. Bảng dưới biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải

Số trung bình cộng của mẫu số liệu ghép nhóm trên là:

$\overline{x}$ = $\frac{25.25+35.20+45.20+55.15+65.14+75.6}{100}$  = 44,1.

Phương sai của mẫu số liệu trên là:

s² = $\frac{1}{100}$ .[25. (25 – 44,1)² + 20. (35 – 44,1)² + 20. (45 – 44,1)²

           +15. (55 – 44,1)² + 14. (65 – 44,1)² + 6.(75 – 44,1)²] ≈ 244,19.

Độ lệch chuẩn của mẫu số liệu trên là: s = $\sqrt{244,19}$  ≈ 15,63.

Học tốt Toán 12 Chương 3

Các bài học để học tốt Bài tập cuối chương 3 Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài tập cuối chương 3

Xem thêm tóm tắt lý thuyết Toán lớp 12 Cánh diều hay khác:

• Lý thuyết Toán 12 Bài 1: Nguyên hàm

• Lý thuyết Toán 12 Bài 2: Nguyên hàm của một số hàm số sơ cấp

• Tổng hợp lý thuyết Toán 12 Chương 3

• Lý thuyết Toán 12 Bài 1: Nguyên hàm

• Lý thuyết Toán 12 Bài 2: Nguyên hàm của một số hàm số sơ cấp

Xem thêm các tài liệu học tốt lớp 12 hay khác:

• Giải sgk Toán 12 Cánh diều
• Giải Chuyên đề học tập Toán 12 Cánh diều
• Giải SBT Toán 12 Cánh diều
• Giải lớp 12 Cánh diều (các môn học)
• Giải lớp 12 Kết nối tri thức (các môn học)
• Giải lớp 12 Chân trời sáng tạo (các môn học)

---