Hoạt động khám phá 9 trang 41 Toán 12 Tập 2 Chân trời sáng tạo

Giải Toán 12 Bài 1: Phương trình mặt phẳng - Chân trời sáng tạo

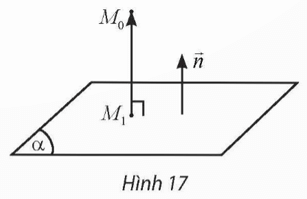
Hoạt động khám phá 9 trang 41 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 và điểm M₀(x₀; y₀; z₀). Gọi M₁(x₁; y₁; z₁) là hình chiếu vuông góc của M₀ trên (α) (Hình 17).

a) Nêu nhận xét về phương của hai vectơ $\overrightarrow{M_1{M}_0}=\left(x_0-x_1;y_0-y_1;z_0-z_1\right)$ và $\overrightarrow{n}=\left(A;B;C\right)$.

b) Tính $\overrightarrow{M_1{M}_0}.\overrightarrow{n}$ theo A, B, C, D và tọa độ của M₀.

c) Giải thích tại sao ta lại có đẳng thức $\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|=\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|$

d) Từ các kết quả trên suy ra cách tính $d\left(M_0,\left(\alpha \right)\right)=\left|\overrightarrow{M_1{M}_0}\right|=\frac{\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|}{\left|\overrightarrow{n}\right|}$

Lời giải:

a) Vì M₁(x₁; y₁; z₁) là hình chiếu vuông góc của M₀ trên (α) nên M₁M₀ ^ (α).

Do đó hai vectơ $\overrightarrow{M_1{M}_0}=\left(x_0-x_1;y_0-y_1;z_0-z_1\right)$ và $\overrightarrow{n}=\left(A;B;C\right)$ cùng phương với nhau.

b) $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=A\left(x_0-x_1\right)+B\left(y_0-y_1\right)+C\left(z_0-z_1\right)$

= Ax₀ + By₀ + Cz₀ – Ax₁ – By₁ – Cz₁.

Vì M₁(x₁; y₁; z₁) Î (α) nên ta có Ax₁ + By₁ + Cz₁ + D = 0 ⇔ D = – Ax₁ – By₁ – Cz₁.

Do đó $\overrightarrow{M_1{M}_0}.\overrightarrow{n}$ = Ax₀ + By₀ + Cz₀ + D.

c) Ta có $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|.\cos \left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)$.

Mà do hai vectơ $\overrightarrow{M_1{M}_0}$ và $\overrightarrow{n}$ cùng phương với nhau nên $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=0°$ hoặc $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=180°$.

+) Nếu $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=0°$ thì $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|$.

+) Nếu $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=180°$ thì $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=-\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|$

Do đó $\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|=\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|$.

d) Vì $\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|=\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|$ nên

$d\left(M_0,\left(\alpha \right)\right)=\left|\overrightarrow{M_1{M}_0}\right|=\frac{\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|}{\left|\overrightarrow{n}\right|}=\frac{\left|A{x}_0+B{y}_0+C{z}_0+D\right|}{\sqrt{A^2+B^2+C^2}}$

Lời giải bài tập Toán 12 Bài 1: Phương trình mặt phẳng hay, chi tiết khác:

• Hoạt động khởi động trang 32 Toán 12 Tập 2: Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ? ....

• Hoạt động khám phá 1 trang 32 Toán 12 Tập 2: a) Cho vectơ $\overrightarrow{n}$ khác $\overrightarrow{0}$. Qua một điểm M₀ cố định trong không gian, có bao nhiêu mặt phẳng (α) vuông góc với giá của vectơ $\overrightarrow{n}$? ....

• Thực hành 1 trang 33 Toán 12 Tập 2: Trong không gian Oxyz, cho ba điểm A(3; 0; 0), B(0; 4; 0), C(0; 0; 5) ....

• Vận dụng 1 trang 33 Toán 12 Tập 2: Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác đều ở Hình 3a được vẽ lại như Hình 3b ....

• Hoạt động khám phá 2 trang 33 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) có cặp vectơ chỉ phương $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$, $\overrightarrow{b}=\left(b_1;b_2;b_3\right)$ ....

• Thực hành 2 trang 34 Toán 12 Tập 2: Cho mặt phẳng (Q) đi qua ba điểm A(1; 1; 1), B(−1; 1; 5), C(10; 7; −1) ....

• Vận dụng 2 trang 34 Toán 12 Tập 2: Cho biết hai vectơ $\overrightarrow{a}=\left(2;1;1\right)$, $\overrightarrow{b}=\left(1;-2;0\right)$có giá lần lượt song song với ngón trỏ ....

• Hoạt động khám phá 3 trang 35 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M₀(1; 2; 3) và nhận $\overrightarrow{n}=\left(7;5;2\right)$ ....

• Thực hành 3 trang 36 Toán 12 Tập 2: Cho hai mặt phẳng (α), (β) có phương trình tổng quát là (α): 2x + 2y – 3z – 4 = 0 và (β): x + 4z – 12 = 0 ....

• Hoạt động khám phá 4 trang 36 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M₀(x₀; y₀; z₀) và nhận $\overrightarrow{n}=\left(A;B;C\right)$ ....

• Hoạt động khám phá 5 trang 36 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M(0; 2; 1) và có cặp vectơ chỉ phương ....

• Hoạt động khám phá 6 trang 37 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt phẳng (α) đi qua ba điểm A(0; 1; 1), B(2; 4; 3), C(5; 3; 1) ....

• Thực hành 4 trang 38 Toán 12 Tập 2: Viết phương trình mặt phẳng (P) trong mỗi trường hợp sau: ....

• Vận dụng 3 trang 38 Toán 12 Tập 2: Trong không gian Oxyz, cho hình lăng trụ OAB.O'A'B'. Biết O là gốc tọa độ, A(2; 0; 0), B(0; 3; 0), O'(0; 0; 5) ....

• Hoạt động khám phá 7 trang 38 Toán 12 Tập 2: Cho hai mặt phẳng (α), (β) có phương trình là (α): x – 2y + 3z + 1 = 0 và (β): 2x – 4y + 6z + 1 = 0 ....

• Thực hành 5 trang 39 Toán 12 Tập 2: Mặt phẳng (E): 2x – y + 8z + 1 = 0 song song với mặt phẳng nào sau đây? ....

• Vận dụng 4 trang 40 Toán 12 Tập 2: Trên bản thiết kế đồ họa 3D của một cách đồng điện mặt trời trong không gian Oxyz, một tấm pin nằm trên mặt phẳng ....

• Hoạt động khám phá 8 trang 40 Toán 12 Tập 2: Cho hai mặt phẳng (α) và (β) có phương trình là (α): 3x + 2y + z + 1 = 0 và (β): 5x – 10y + 5z + 9 = 0 ....

• Thực hành 6 trang 40 Toán 12 Tập 2: Tìm các cặp mặt phẳng vuông góc trong các mặt phẳng sau ....

• Vận dụng 5 trang 40 Toán 12 Tập 2: Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không ....

• Thực hành 7 trang 42 Toán 12 Tập 2: a) Tính chiều cao của hình chóp O.MNP với tọa độ các đỉnh là O(0; 0; 0), M(2; 1; 2), N(3; 3; 3), P(4; 5; 6) ....

• Vận dụng 6 trang 42 Toán 12 Tập 2: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng $a\sqrt{2}$, chiều cao bằng 2a và O là tâm của đáy ....

• Bài 1 trang 42 Toán 12 Tập 2: Viết phương trình của mặt phẳng: Đi qua điểm A(2; 0; 0) và nhận $\overrightarrow{n}=\left(2;1;-1\right)$ làm vectơ pháp tuyến; ....

• Bài 2 trang 42 Toán 12 Tập 2: a) Lập phương trình của các mặt phẳng tọa độ (Oxy), (Oyz), (Oxz) ....

• Bài 3 trang 42 Toán 12 Tập 2: Cho tứ diện ABCD có các đỉnh A(4; 0; 2), B(0; 5; 1), C(4; −1; 3), D(3; −1; 5 ....

• Bài 4 trang 42 Toán 12 Tập 2: Viết phương trình mặt phẳng (Q) đi qua C(1; −5; 0) và song song với mặt phẳng (P): 3x – 5y + 4z – 2024 = 0 ....

• Bài 5 trang 42 Toán 12 Tập 2: Viết phương trình mặt phẳng (α) đi qua hai điểm A(1; 0; 1), B(5; 2; 3) và vuông góc với mặt phẳng (β): 2x – y + z – 7 = 0 ....

• Bài 6 trang 42 Toán 12 Tập 2: Viết phương trình mặt phẳng (R) đi qua điểm A(1; 2; −1) và vuông góc với hai mặt phẳng (P): 4x – 2y + 6z – 11 = 0, (Q): 2x + 2y + 2z – 7 = 0 ....

• Bài 7 trang 43 Toán 12 Tập 2: Tính khoảng cách từ gốc tọa độ và từ điểm M(1; −2; 13) đến mặt phẳng (P): 2x – 2y – z + 3 = 0 ....

• Bài 8 trang 43 Toán 12 Tập 2: Tính khoảng cách giữa hai mặt phẳng song song (P): x – 2 = 0 và (Q): x – 8 = 0 ....

• Bài 9 trang 43 Toán 12 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = 5a, SA = 3a và SA ⊥ (ABCD). ....

• Bài 10 trang 43 Toán 12 Tập 2: Một công trường xây dựng nhà cao tầng đã thiết lập hệ tọa độ Oxyz ....

Xem thêm lời giải bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

• Toán 12 Bài 2: Phương trình đường thẳng trong không gian

• Toán 12 Bài 3: Phương trình mặt cầu

• Toán 12 Bài tập cuối chương 5

• Toán 12 Bài 1: Xác suất có điều kiện

• Toán 12 Bài 2: Công thức xác suất toàn phần và công thức Bayes

Xem thêm các tài liệu học tốt lớp 12 hay khác:

• Giải sgk Toán 12 Chân trời sáng tạo
• Giải Chuyên đề học tập Toán 12 Chân trời sáng tạo
• Giải SBT Toán 12 Chân trời sáng tạo
• Giải lớp 12 Chân trời sáng tạo (các môn học)
• Giải lớp 12 Kết nối tri thức (các môn học)
• Giải lớp 12 Cánh diều (các môn học)

---