Giải Toán 9 trang 11 Tập 1 Cánh diều

Với Giải Toán 9 trang 11 Tập 1 trong Bài 1: Phương trình quy về phương trình bậc nhất một ẩn Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 11.

Giải Toán 9 trang 11 Tập 1 Cánh diều

Bài 1 trang 11 Toán 9 Tập 1: Giải các phương trình:

a) (9x – 4)(2x + 5) = 0;

b) (1,3x + 0,26)(0,2x – 4) = 0;

c) 2x(x + 3) – 5(x + 3) = 0;

d) x² – 4 + (x + 2)(2x – 1) = 0.

Lời giải:

a) Để giải được phương trình (9x – 4)(2x + 5) = 0, ta giải hai phương trình sau:

9x – 4 = 0 9x = 4 $x=\frac{4}{9};$

2x + 5 = 0 2x = –5 $x=-\frac{5}{2}.$

Vậy phương trình đã cho có hai nghiệm là $x=\frac{4}{9}$ và $x=-\frac{5}{2}.$

b) Để giải được phương trình (1,3x + 0,26)(0,2x – 4) = 0, ta giải hai phương trình sau:

1,3x + 0,26 = 0            1,3x = –0,26                 x = –0,2;

0,2x – 4 = 0       0,2x = 4           x = 20.

Vậy phương trình đã cho có hai nghiệm là x = –0,2 và x = 20.

c) 2x(x + 3) – 5(x + 3) = 0

    (x + 3)(2x – 5) = 0.

Để giải được phương trình (x + 3)(2x – 5) = 0, ta giải hai phương trình sau:

x + 3 = 0       x = –3;

2x – 5 = 0       2x = 5    $x=\frac{5}{2}.$

Vậy phương trình đã cho có hai nghiệm là x = –3 và $x=\frac{5}{2}.$

d) x² – 4 + (x + 2)(2x – 1) = 0

(x – 2)(x + 2) + (x + 2)(2x – 1) = 0

(x + 2)(x – 2 + 2x – 1) = 0

(x + 2)(3x – 3) = 0.

Để giải được phương trình (x + 2)(3x – 3) = 0, ta giải hai phương trình sau:

x + 2 = 0       x = –2;

3x – 3 = 0       3x = 3         x = 1.

Vậy phương trình đã cho có hai nghiệm là x = –2 và x = 1.

Bài 2 trang 11 Toán 9 Tập 1: Giải các phương trình:

a) $\frac{1}{x}=\frac{5}{3\left(x+2\right)};$

b) $\frac{x}{2x-1}=\frac{x-2}{2x+5};$

c) $\frac{5x}{x-2}=7+\frac{10}{x-2};$

d) $\frac{x^2-6}{x}=x+\frac{3}{2}.$

Lời giải:

a) $\frac{1}{x}=\frac{5}{3\left(x+2\right)}.$

Điều kiện xác định: x ≠ 0 và x ≠ –2.

$\frac{1}{x}=\frac{5}{3\left(x+2\right)}$

$\frac{3\left(x+2\right)}{3x\left(x+2\right)}=\frac{5x}{3x\left(x+2\right)}$

   3(x + 2) = 5x

      3x + 6 = 5x

           –2x = –6

               x = 3.

Ta thấy x = 3 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm x = 3.

b) $\frac{x}{2x-1}=\frac{x-2}{2x+5}.$

Điều kiện xác định: $x\ne \frac{1}{2}$ và $x\ne -\frac{5}{2}.$

$\frac{x}{2x-1}=\frac{x-2}{2x+5}$

$\frac{x\left(2x+5\right)}{\left(2x-1\right)\left(2x+5\right)}=\frac{\left(x-2\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x+5\right)}$

           x(2x + 5) = (x – 2)(2x – 1)

            2x² + 5x = 2x² – x – 4x + 2

2x² + 5x – 2x² + x + 4x = 2

                               10x = 2

                                $x=\frac{1}{5}.$

Ta thấy $x=\frac{1}{5}$ thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm $x=\frac{1}{5}.$

c) $\frac{5x}{x-2}=7+\frac{10}{x-2}.$

Điều kiện xác định: x ≠ 2.

$\frac{5x}{x-2}=7+\frac{10}{x-2}$

$\frac{5x}{x-2}=\frac{7\left(x-2\right)}{x-2}+\frac{10}{x-2}$

5x = 7(x – 2) + 10

     5x = 7x – 14 + 10

5x – 7x = –4

      –2x = –4

          x = 2.

Ta thấy x = 2 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm x = 2.

d) $\frac{x^2-6}{x}=x+\frac{3}{2}.$

Điều kiện xác định: x ≠ 0.

$\frac{x^2-6}{x}=x+\frac{3}{2}$

$\frac{\left(x^2-6\right)\cdot 2}{2x}=\frac{x\cdot 2x}{2x}+\frac{3x}{2x}$

(x² – 6).2 = x.2x + 3x

   2x² – 12 = 2x² + 3x

2x² – 2x² – 3x = 12

                 –3x = 12

                     x = –4.

Ta thấy x = –4 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm x = –4.

Bài 3 trang 11 Toán 9 Tập 1: Một ca nô đi xuôi dòng từ địa điểm A đến địa điểm B, rồi lại đi ngược dòng từ địa điểm B trở về địa điểm A. Thời gian cả đi và về là 3 giờ. Tính tốc độ của dòng nước. Biết tốc độ của ca nô khi nước yên lặng là 27 km/h và độ dài quãng đường AB là 40 km.

Lời giải:

Gọi tốc độ của dòng nước là x (km/h) (0 < x < 27).

Khi đó, tốc độ của ca nô khi đi xuôi dòng là 27 + x (km/h) và tốc độ của ca nô khi đi ngược dòng là 27 – x (km/h).

Thời gian ca nô đi xuôi dòng quãng đường AB là $\frac{40}{27+x}$(giờ).

Thời gian ca nô đi ngược dòng quãng đường AB là $\frac{40}{27-x}$(giờ).

Theo bài, thời gian cả đi và về là 3 giờ nên ta có phương trình: $\frac{40}{27+x}+\frac{40}{27-x}=3.$

Giải phương trình:

                               $\frac{40}{27+x}+\frac{40}{27-x}=3$

            $\frac{40\left(27-x\right)}{\left(27+x\right)\left(27-x\right)}+\frac{40\left(27+x\right)}{\left(27+x\right)\left(27-x\right)}=\frac{3\left(27+x\right)\left(27-x\right)}{\left(27+x\right)\left(27-x\right)}$

                     40(27 – x) + 40(27 + x) = 3(27 + x)(27 – x)

                 1 080 – 40x + 1 080 + 40x = 3(729 – x²)

                 1 080 – 40x + 1 080 + 40x = 2 187 – 3x²

1 080 – 40x + 1 080 + 40x – 2 187 + 3x² = 0

                                                    3x² – 27 = 0

                                                        x² – 9 = 0

                                            (x – 3)(x + 3) = 0

                                             x – 3 = 0 hoặc x + 3 = 0

                                                   x = 3 hoặc x = –3.

Do 0 < x < 27 nên x = 3.

Vậy tốc độ của dòng nước là 3 km/h.

Bài 4 trang 11 Toán 9 Tập 1: Một doanh nghiệp sử dụng than làm chất đốt trong quá trình sản xuất sản phẩm. Doanh nghiệp đó lập kế hoạch tài chính cho việc loại bỏ chất ô nhiễm trong khí thải theo dự kiến sau: Để loại bỏ p% chất ô nhiễm trong khí thải thì chi phí C (triệu đồng) được tính theo công thức $C=\frac{80p}{100-p}$ với 0 ≤ p < 100 (Nguồn: Intermediate Algebra, Fifth Edition, Ron Larson, năm 2009). Với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được bao nhiêu phần trăm chất gây ô nhiễm trong khí thải?

Lời giải:

Với chi phí là 420 triệu đồng thì ta có C = 420, tức là ta có phương trình: $\frac{80p}{100-p}=420.$

Giải phương trình:

$\frac{80p}{100-p}=420$

$\frac{80p}{100-p}=\frac{420\left(100-p\right)}{100-p}$

      80p = 42 000 – 420p

80p + 420p = 42 000

          500p = 42 000

                p = 84 (thỏa mãn điều kiện 0 ≤ p < 100).

Vậy với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được 84% chất gây ô nhiễm trong khí thải.

Bài 5 trang 11 Toán 9 Tập 1: Bạn Hoa dự định dùng hết số tiền 600 nghìn đồng để mua một số chiếc áo đồng giá tặng các bạn có hoàn cảnh khó khăn. Khi đến cửa hàng, loại áo mà bạn Hoa dự định mua được giảm giá 30 nghìn đồng/chiếc. Do vậy, bạn Hoa đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định. Tính giá tiền của mỗi chiếc áo mà bạn Hoa đã mua.

Lời giải:

Gọi giá tiền của mỗi chiếc áo mà bạn Hoa dự định mua là x (nghìn đồng) (x > 30).

Giá tiền của chiếc áo sau khi giảm giá 30 nghìn đồng/chiếc là x – 30 (nghìn đồng).

Số chiếc áo bạn Hoa dự định mua là $\frac{600}{x}$(chiếc).

Số chiếc áo bạn Hoa đã mua thực tế là $\frac{600}{x-30}$(chiếc).

Theo bài, thực tế bạn Hoa đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định nên ta có phương trình: $\frac{600}{x-30}=\mathrm{1,25}\cdot \frac{600}{x}.$

Giải phương trình:

$\frac{600}{x-30}=\mathrm{1,25}\cdot \frac{600}{x}$

$\frac{1}{x-30}=\frac{\mathrm{1,25}}{x}$

$\frac{x}{x\left(x-30\right)}=\frac{\mathrm{1,25}\left(x-30\right)}{x\left(x-30\right)}$

x = 1,25(x – 30)

x = 1,25x – 37,5

1,25x – x = 37,5

0,25x = 37,5

x = 150 (thỏa mãn điều kiện x > 30).

Do đó, giá tiền của mỗi chiếc áo mà bạn Hoa dự định mua là 150 nghìn đồng.

Giá tiền mỗi chiếc áo mà bạn Hoa đã mua là: 150 – 30 = 120 nghìn đồng.

Vậy giá tiền mỗi chiếc áo mà bạn Hoa đã mua là 120 nghìn đồng.

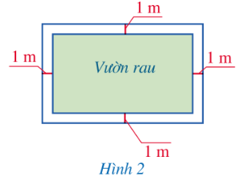
Bài 6 trang 11 Toán 9 Tập 1: Một mảnh đất có dạng hình chữ nhật với chu vi bằng 52 m. Trên mảnh đất đó, người ta làm một vườn rau có dạng hình chữ nhật với diện tích là 112 m² và một lối đi xung quanh vườn rộng 1 m (Hình 2). Tính các kích thước của mảnh đất đó.

Lời giải:

Nửa chu vi của mảnh đất hình chữ nhật là 52 : 2 = 26 (m).

Gọi chiều rộng của mảnh đất hình chữ nhật là x (m) (x < 13).

Khi đó, chiều dài của mảnh đất hình chữ nhật là 26 – x (m).

Chiều rộng của vườn rau là x – 1 – 1 = x – 2 (m).

Chiều dài của vườn rau là 26 – x – 1 – 1 = 24 – x (m).

Diện tích của vườn rau là (x – 2)(24 – x) (m²).

Theo bài, vườn rau có dạng hình chữ nhật với diện tích là 112 m² nên ta có phương trình: (x – 2)(24 – x) = 112.

Giải phương trình:

                (x – 2)(24 – x) = 112

24x – x² – 48 + 2x – 112 = 0

             – x² + 26x – 160 = 0

                x² – 26x + 160 = 0

      x² – 10x – 16x + 160 = 0

 (x² – 10x) – (16x – 160) = 0

    x(x – 10) – 16(x – 10) = 0

              (x – 10)(x – 16) = 0

              x – 10 = 0 hoặc x – 16 = 0

                    x = 10 hoặc x = 16.

Do x < 13 nên x = 10.

Vậy mảnh đất có chiều rộng là 10 m và chiều dài là 26 – 10 = 16 m.

Lời giải bài tập Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn hay khác:

• Giải Toán 9 trang 5
• Giải Toán 9 trang 7
• Giải Toán 9 trang 8

Xem thêm lời giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

• Toán 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

• Toán 9 Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

• Toán 9 Bài tập cuối chương 1

• Toán 9 Bài 1: Bất đẳng thức

• Toán 9 Bài 2: Bất phương trình bậc nhất một ẩn

Xem thêm các tài liệu học tốt lớp 9 hay khác:

• Giải sgk Toán 9 Cánh diều
• Giải SBT Toán 9 Cánh diều
• Giải lớp 9 Cánh diều (các môn học)
• Giải lớp 9 Kết nối tri thức (các môn học)
• Giải lớp 9 Chân trời sáng tạo (các môn học)

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---