Lý thuyết Giá trị lượng giác của một cung lớp 10 (hay, chi tiết)

---

---

Bài viết Lý thuyết Giá trị lượng giác của một cung lớp 10 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm Giá trị lượng giác của một cung.

Lý thuyết Giá trị lượng giác của một cung

(199k) Xem Khóa học Toán 10 KNTTXem Khóa học Toán 10 CDXem Khóa học Toán 10 CTST

Bài giảng: Bài 2: Giá trị lượng giác của một cung - Thầy Lê Thành Đạt (Giáo viên VietJack)

I. GIÁ TRỊ LƯỢNG GIÁC CỦA CUNG α

1. Định nghĩa

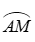
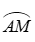
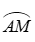
Trên đường tròn lượng giác cho cung có sđ = α (còn viết = α)

Tung độ y = 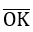của điểm M gọi là sin của α và kí hiệu là sinα

sin α =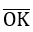

Hoành độ x = 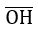của điểm M gọi là côsin của α và kí hiệu là cosα

cos α =

Nếu cos α ≠ 0, tỉ số 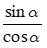gọi là tang của α và kí hiệu là tan α (người ta còn dùng kí hiệu tg α)

Tan α =

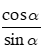
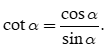
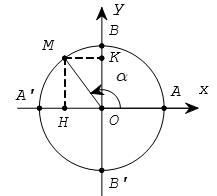Nếu sinα ≠ 0 tỉ số gọi là côtang của α và kí hiệu là cotα (người ta còn dùng kí hiệu cotg α)

Các giá trị sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của cung α. Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin

2. Hệ quả

1) sinα và cosα xác định với mọi α ∈ R. Hơn nữa, ta có

sin(α + k2π) = sin α, ∀k ∈ Z;

cos(α + k2π) = cos α, ∀k ∈ Z

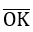
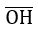
2) Vì –1 ≤ ≤ 1; –1 ≤ ≤ 1 nên ta có

–1 ≤ sin α ≤ 1

–1 ≤ cos α ≤ 1

3) Với mọi m ∈ R mà –1 ≤ m ≤ 1 đều tồn tại α và β sao cho sin α = m và cos β = m.

4) tanα xác định với mọi α ≠ 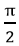+ kπ (k ∈ Z)

5) cotα xác định với mọi α ≠ kπ (k ∈ Z)

6) Dấu của các giá trị lượng giác của góc α phụ thuộc vào vị trí điểm cuối của cung = α trên đường tròn lượng giác.

Bảng xác định dấu của các giá trị lượng giác

Giá trị lượng giác |Góc phần tư	I	II	III	IV
cos α	+	-	-	+
sin α	+	+	-	-
tan α	+	-	+	-
cot α	+	-	+	-

3. Giá trị lượng giác của các cung đặc biệt

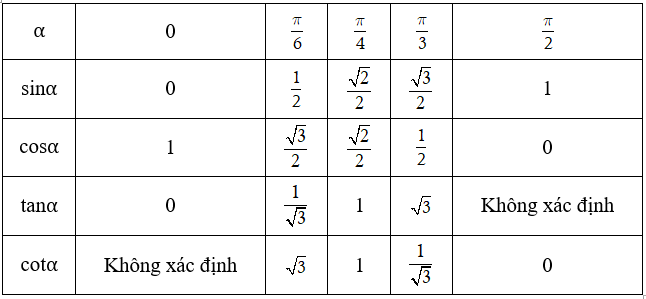
II. Ý NGHĨA HÌNH HỌC CỦA TANG VÀ CÔTANG

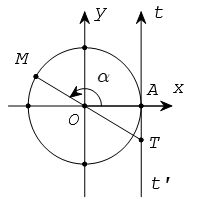
1. Ý nghĩa hình học của tan α

Từ A vẽ tiếp tuyến t’At với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại A.

Gọi T là giao điểm của OM với trục t’At.

tanα được biểu diễn bởi độ dài đại số của vectơ 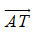trên trục t’At. Trục t’At được gọi là trục tang.

2. Ý nghĩa hình học của cot α

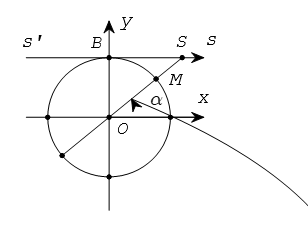
Từ B vẽ tiếp tuyến s’Bs với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại B.

Gọi S là giao điểm của OM với trục s’Bs

cot α được biểu diển bởi độ dài đại số của vectơ 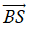trên trục s’Bs. Trục s’Bs được gọi là trục côtang.

III – QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC

1. Công thức lượng giác cơ bản

Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau

sin²α + cos²α = 1

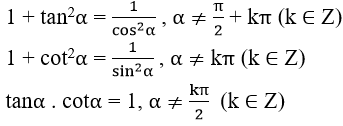
2. Giá trị lượng giác của các cung có liên quan đặc biệt

1) Cung đối nhau: α và –α

cos(-α) = cosα

sin(-α) = –sinα

tan(-α) = –tanα

cot(-α) = –cotα

2) Cung bù nhau: α và π-α

sin(π-α) = sinα

cos(π-α) = –cosα

tan(π-α) = –tanα

cot(π-α) = –cotα

3) Cung hơn kém π : α và (α + π)

sin(α + π) = –sinα

cos(α + π) = –cosα

tan(α + π) = tanα

cot(α + π) = cotα

4) Cung phụ nhau: α và ( 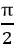– α)

sin(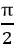 – α) = cos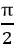α

cos( – α) = sinα

tan(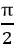 – α) = cot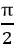α

cot( – α) = tanα

(199k) Xem Khóa học Toán 10 KNTTXem Khóa học Toán 10 CDXem Khóa học Toán 10 CTST

Xem thêm các dạng bài tập Toán 10 có đáp án hay khác:

• Lý thuyết Cung và góc lượng giác
• Lý thuyết Công thức lượng giác
• Lý thuyết Tổng hợp chương Cung và góc lượng giác. Công thức lượng giác

Để học tốt lớp 10 các môn học sách mới:

• Giải bài tập Lớp 10 Kết nối tri thức
• Giải bài tập Lớp 10 Chân trời sáng tạo
• Giải bài tập Lớp 10 Cánh diều

---

---

---