Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán chuyển động

Bài viết Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán chuyển động với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán chuyển động.

Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán chuyển động

A. Phương pháp giải

* Các bước giải bài toán bằng cách lập phương trình:

Bước 1: Lập phương trình

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

- Biểu diễn các đại lượng chưa biết khác theo ẩn và các đại lượng đã biết.

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình

Bước 3: Trả lời

Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.

* Các đại lượng liên quan trong bài toán chuyển động: quãng đường (s), vận tốc(v), thời gian (t)

Công thức liên quan: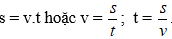

B. Ví dụ minh họa

Ví dụ 1: Một xe vận tải đi từ địa điểm A đến địa điểm B với vận tốc 50 km/h, rồi từ B quay ngay về A với vận tốc 40 km/h. Cả đi và về mất một thời gian là 5 giờ 24 phút. Tìm chiều dài quãng đường từ A đến B.

Lời giải:

Ví dụ 2: Một xe đạp khởi hành từ điểm A, chạy với vận tốc 20 km/h. Sau đó 3 giờ, một xe hơi đuổi theo với vận tốc 50 km/h. Hỏi xe hơi chạy trong bao lâu thì đuổi kịp xe đạp?

Lời giải:

Gọi thời gian xe hơi bắt đầu chạy đến khi gặp xe đạp là x giờ (x > 0)

Thời gian xe đạp đi đến khi gặp xe hơi là x + 3 (h)

Quãng đường xe hơi đi được là 50x(km), quãng đường xe đạp đi được là 20(x + 3) (km)

Vì cả hai xe cùng đi từ A đến khi gặp nhau thì quãng đường hai xe đi được là bằng nhau nên ta có phương trình:

50x = 20(x + 3)

⇔ 50x = 20x + 60

⇔ 30x = 60

⇔ x = 2 (tm đk)

Vậy xe hơi chạy trong 2 giờ sẽ đuổi kịp xe đạp.

Ví dụ 3: Lúc 6 giờ 15 phút, một ô tô đi từ A để đến B với vận tốc 70 km/h. Khi đến B, ô tô nghỉ 1 giờ rưỡi, rồi quay về A với vận tốc 60 km/h và đến A lúc 11 giờ cùng ngày. Tính quãng đường AB.

Lời giải:

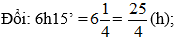
Tổng thời gian xe ô tô đi từ A đến B và đi từ B về A (không tính thời gian nghỉ) là:

  

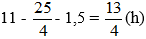
Gọi độ dài quãng đường AB là x km (x > 0)

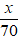
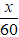
Thời gian xe ô tô đi từ A đên B là (h), thời gian ô tô đi từ B về A là (h)

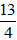
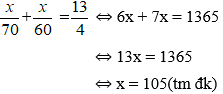
Tổng thời gian đi của xe là giờ nên ta có phương trình:

Vậy độ dài quãng đường AB là 105km.

C. Bài tập vận dụng

Bài 1: Một người đi xe đạp từ địa điểm A đến địa điểm B với vận tốc 15km/h và sau đó quay trở về từ B đến A với vận tốc 12km/h. Cả đi lẫn về mất 4 giờ 30 phút. Tính chiều dài quãng đường.

Lời giải:

Đổi 4h30’ = 4,5h

Gọi độ dài quãng đường AB là x km (x > 0)

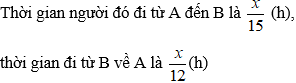
Tổng thời gian đi của xe đạp là 4,5 giờ nên ta có phương trình:

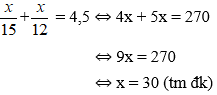
Vậy độ dài quãng đường AB là 30km.

Bài 2: Lúc 7 giờ. Một ca nô xuôi dòng từ A đến B cách nhau 36km rồi ngay lập tức quay về bên A lúc 11 giờ 30 phút. Tính vận tốc của ca nô khi xuôi dòng. Biết rằng vận tốc nước chảy là 6km/h.

Lời giải:

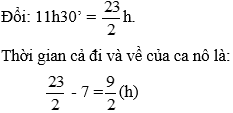
Gọi vận tốc riêng của ca nô khi nước lặng yên là x (km/h) (x > 6)

Vận tốc của ca nô khi xuôi dòng là x + 6 (km/h)

Vận tốc của ca nô khi ngược dòng là x - 6(km/h)

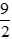
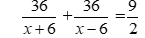
Vì tổng thời gian cả đi và về là (h) nên ta có phương trình:

⇒ 36(x – 6).2 + 36(x + 6).2 = 9(x + 6)(x – 6)

⇔ 72x – 72.6+ 72x + 72.6 = 9x² - 9.36

⇔ 9x² – 144x – 9.36 = 0

⇔ x² – 16x – 36 = 0

⇔ (x + 2)(x – 18) = 0

⇔ x + 2 = 0 hoặc x – 18 = 0

⇔ x = -2 hoặc x = 18

Vì x = - 2 không TMĐK x > 6 nên vận tốc riêng của ca nô là 18km/h.

Vậy vận tốc của ca nô khi xuôi dòng là 18 + 6 = 24 km/h

Bài 3: Một ca nô xuôi dòng từ bến A đến bến B mất 4 giờ, và ngược dòng từ bến B đến bến A mất 5h. Tính khoảng cách giữa hai bến, biết vận tốc dòng nước là 2 km/h.

Lời giải:

Gọi vận tốc riêng của ca nô là x km/h(x > 2)

Vận tốc của ca nô khi xuôi dòng là x + 2 (km/h)

Vận tốc của ca nô khi ngược dòng là x - 2(km/h)

Quãng đường khi xuôi dòng của ca nô là 4(x + 2)(km). quãng đường khi ngược dòng của ca nô là 5(x – 2)(km)

Vì quãng đường đi của ca nô khi xuôi dòng và khi ngược dòng là như nhau nên ta có phương trình:

4(x + 2) = 5(x – 2)

⇔ 4x + 8 = 5x - 10

⇔ x = 18 (tmđk)

Vậy khoảng cách giữa hai bến A và B là 4(18 + 2) = 80km.

Bài 4: Một người đi xe đạp từ A đến B với vận tốc trung bình 12km/h. Khi đi về từ B đến A. Người đó đi với vận tốc trung bình là 10 km/h, nên thời gian về nhiều hơn thời gian đi là 15 phút. Tính độ dài quãng đường AB.

Lời giải:

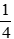
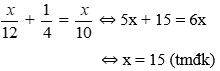
Vì thời gian về nhiều hơn thời gian đi là giờ nên ta có phương trình.

Vậy độ dài quãng đường AB là 15km

Bài 5: Một người đi xe máy từ A đến B với vận tốc 30 km/h. Đến B người đó làm việc trong một giờ rồi quay về A với vận tốc 24 km/h. Biết thời gian tổng cộng hết 5 giờ 30 phút. Tính quãng đường AB.

Lời giải:

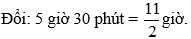
Tổng thời gian xe đi từ A đến B và đi từ B về A (không tính thời gian làm việc tại B) là: 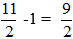(giờ)

Gọi độ dài quãng đường AB là x km (x >0)

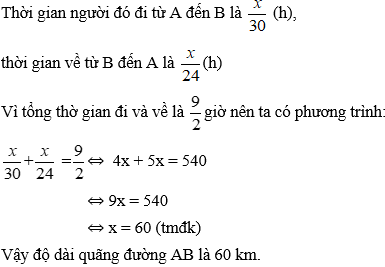
Bài 6: Một bạn học sinh đi học từ nhà đến trường với vận tốc trung bình 4 km/h. Sau khi đi được 2/3 quãng đường bạn ấy đã tăng vận tốc lên 5 km/h. Tính quãng đường từ nhà đến trường của bạn học sinh đó, biết rằng thời gian bạn ấy đi từ nhà đến trường là 28 phút.

Lời giải:

Gọi quãng đường từ nhà đến trường của bạn học sinh là x km(x > 0)

Bài 7: Một xe ô tô đi từ A đến B hết 3 giờ 12 phút. Nếu vận tốc tăng thêm 10 km/h thì đến B sớm hơn 32 phút. Tính quãng đường AB và vận tốc ban đầu của xe.

Lời giải:

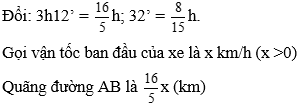
Khi tăng thêm 10km/h thì vận tốc mới của xe là x + 10 (km/h), khi đó xe đi hết thời gian là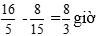

Ta có phương trình:

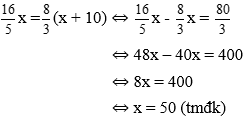
Vậy vận tốc ban đầu của xe là 50km/h. quãng đường AB là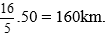

Bài 8: Một người đi từ A đến B, nếu đi bằng xe máy thì mất thời gian là 3 giờ 30 phút, còn đi bằng ô tô thì mất thời gian là 2 giờ 30 phút. Tính quãng đường AB, biết rằng vận tốc ôtô lớn hơn vận tốc xe máy là 20 km/h.

Lời giải:

Đổi: 3 giờ 30 phút = 3,5 giờ; 2 giờ 30 phút = 2,5 giờ.

Gọi độ dài quãng đường AB là x km (x >0)

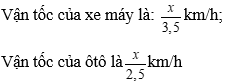
Vì vận tốc ôtô lớn hơn vận tốc xe máy là 20 km/h nên ta có phương trình:

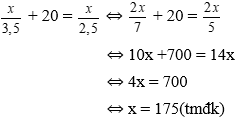
Vậy độ dài quãng đường AB là 175km.

Bài 9: Một người đi xe gắn máy, đi từ địa điểm A đến địa điểm B trên một quãng đường dài 35km. Lúc trở về người đó đi theo con đường khác dài 42km với vận tốc kém hơn vận tốc lượt đi là 6 km/h. Thời gian lượt về bằng 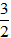thời gian lượt đi. Tìm vận tốc lượt đi và lượt về.

Lời giải:

Gọi vận tốc của người đó khi đi là x km/h(x > 6)

Vận tốc khi về là x – 6 (km/h)

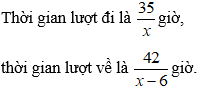
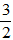
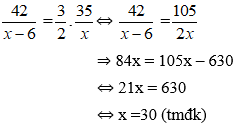
Vì thời gian lượt về bằng thời gian lượt đi nên ta có phương trình:

Vậy vận tốc lượt đi của người đó là 30km/h, vân tốc lượt về là 24km/h

Bài 10: Một xe tải đi từ A đến B với vận tốc 50 km/h. Đi được 24 phút thì gặp đường xấu nên vận tốc trên quãng đường còn lại giảm còn 40 km/h. Vì vậy đã đến nơi chậm mất 18 phút. Tìm chiều dài quãng đường từ A đến B.

Lời giải:

Vì thời gian thực tế đi chậm hơn thời gian dự định là 18 phút nên ta có phương trình:

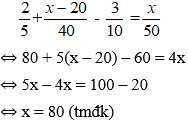
Vậy chiều dài quãng đường AB là 80km.

Bài 11: Một chiếc thuyền đi xuôi dòng từ bến A đến bến B hết 5 giờ, ngược dòng từ bến B về bến A hết 7 giờ. Hỏi một đám bèo trôi theo dòng sông từ A đến B hết bao lâu?

Lời giải:

Ta có vận tốc trôi của đám bèo chính là vận tốc của dòng nước.

Gọi thời gian cụm bèo trôi từ bến A về bến B là x giờ (x > 0).

Quãng đường đi từ bến A đến bến B là AB

Vận tốc cụm bèo trôi hay chính là vận tốc chảy của dòng nước là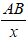

Vì vận tốc của thuyền khi xuôi dòng bằng tổng vận tốc thực của thuyền và vận tốc dòng nước. Vận tốc của thuyền khi ngược dòng bằng hiệu vận tốc thực của thuyền và vận tốc dòng nước. Do đó hiệu vận tốc lúc xuôi dòng và lúc ngược dòng của chiếc thuyền bằng hai lần vận tốc dòng nước.

Từ đó ta có phương trình:

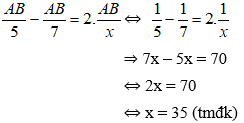
Vậy thời gian cụm bèo trôi từ bến A về bến B là 35 giờ.

Xem thêm các dạng bài tập Toán lớp 8 chọn lọc, có đáp án hay khác:

• Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán so sánh, thêm bớt
• Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán tìm số tự nhiên
• Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất
• Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán hình học, vật lí, hóa học

Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:

• Giải bài tập Toán 8
• Giải sách bài tập Toán 8
• Top 75 Đề thi Toán 8 có đáp án

---