Cách viết phương trình dao động của Con lắc đơn (hay, chi tiết)

---

---

Bài viết Cách viết phương trình dao động của Con lắc đơn với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Cách viết phương trình dao động của Con lắc đơn.

Cách viết phương trình dao động của Con lắc đơn (hay, chi tiết)

A. Phương pháp & Ví dụ

1. Phương pháp

Phương trình dao động con lắc đơn: S = S_ocos(ωt + Φ) hoặc a = a_ocos(ωt + j)(rad)

Bước 1: Tìm t

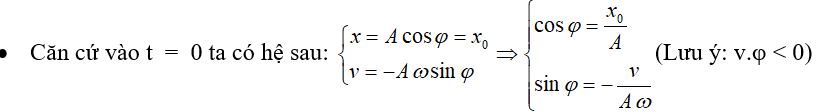
Chú ý: t = 0, vật đi theo chiều (+) thì và ngược lại nếu vật đi theo chiều (-) thì φ > 0

Bước 2: Tìm ω > 0 nếu các đáp án khác nhau về ω

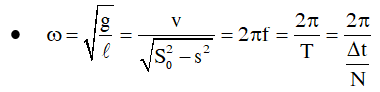
Bước 3: Tìm S_o > 0 nếu các đáp án khác nhau về S_o

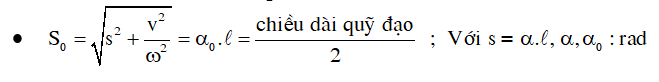
2. Ví dụ

Ví dụ 1: Con lắc đơn có T = 2s. Trong quá trình dao động, góc lệch cực đại của dây là 0,04 rad. Chọn gốc thời gian là lúc vật có li độ là α = 0,02 rad và đang chuyển động về VTCB. PHương trình dao động của con lắc là

A. α = 0,04cos(πt+π/3)(rad).          B. α = 0,04cos(πt-π/3)(rad).

C. α = 0,04cos(πt+2π/3)(rad).          D. α = 0,04cos(πt-2π/3)(rad).

Lời giải:

t = 0 ⇒

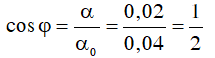
Vật đang ở li độ góc dương đi về VTCB tức là đi theo chiều (-)

⇒ φ = π/3 > 0

Ví dụ 2: Một con lắc đơn được kích thích và để cho dao động tự do với biên độ góc nhỏ trong điều kiện lực cản không đáng kể thì dao động điều hòa với tần số 0,25Hz. Con lắc dao động với biên độ 4cm. Chọn gốc thời gian là lúc con lắc qua VTCB theo chiều dương thì biểu thức li độ góc α là

A. α = 0,04cos(πt-π/2) (rad).          B. α = 0,01cos(πt-π/2) (rad).

C. α = 0,16cos(πt) (rad).          D. α = 0,04cos(πt) (rad).

Lời giải:

B. Bài tập trắc nghiệm

Câu 1. Một con lắc đơn có chiều dài l = 16 cm. Kéo con lắc lệch khỏi vị trí cân bằng một góc 9° rồi thả nhẹ. Bỏ qua mọi ma sát, lấy g = 10 m/s², π² = 10. Chọn gốc thời gian lúc thả vật, chiều dương cùng chiều với chiều chuyển động ban đầu của vật. Viết phương trình dao động theo li độ góc tính ra rad.

A. α = 0,157cos(2,5π + π) rad

B. α = 0,314cos(2,5π + π/2) rad

C. α = 0,314cos(5π - π/2) rad

D. α = 0,157cos(5π + π) rad

Lời giải:

Ta có:

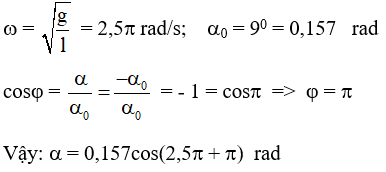
Chọn A

Câu 2. Một con lắc đơn dao động điều hòa với chu kì T = 2 s. Lấy g = 10 m/s², π² = 10. Viết phương trình dao động của con lắc theo li độ dài. Biết rằng tại thời điểm ban đầu vật có li độ góc α = 0,05 rad và vận tốc v = - 15,7 cm/s

A. s = 5√2cos(2πt - π/4) cm

B. s = 5cos(πt + 3π/4) cm

C. s = 5cos(2πt - π/4) cm

D. s = 5√2cos(πt + π/4) cm

Lời giải:

Ta có:

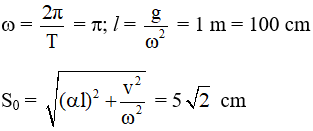
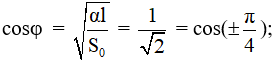
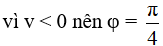
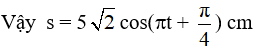
Chọn D

Câu 3. Một con lắc đơn treo một vật nặng có khối lượng 100 g, chiều dài dây treo là 1 m, treo tại nơi có g = 9,86 m/s². Bỏ qua mọi ma sát. Kéo con lắc lệch khỏi vị trí cân bằng góc α₀ rồi thả không vận tốc đầu. Biết con lắc dao động điều hòa với năng lượng W = 8.10^-4 J. Lập phương trình dao động điều hòa của con lắc, chọn gốc thời gian lức vật nặng có li độ cực đại dương. Lấy π² = 10

A. s = 2cosπt cm

B. s = 4cos(πt + π) cm

C. s = 4cosπt cm

D. s = 2cos(πt + π/3) cm

Lời giải:

Phương trình dao động: s = S₀cos(ωt + φ)

Tần số góc ω = √(g/l) = √(9,86) = π rad

Từ W = (mω²S₀²)/2 suy ra biên độ dao động S₀

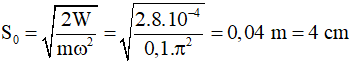
Tìm φ : t = 0, s = S₀ ⇒ cosφ = 1 ⇒ φ = 0. Vậy s = 4cosπt cm. Chọn C.

Câu 4. Một con lắc đơn dài l = 20 cm treo tại một điểm có định. Kéo con lắc khỏi phương thẳng đứng một góc bằn 0,1 rad về phía bên phải rồi chuyền cho một vận tốc 14 cm/s theo phương vuông góc với dây về phía vi trí cân bằng. Coi con lắc dao động điều hòa, viết phương trình dao động đối với li độ dài của con lắc. Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng từ vị trí cân bằng sang phía bên phải, gốc thời gian là lúc con lắc đi qua vị trí cân bằng lần thứ nhất. Cho gia tốc trọng trường g = 9,8 m/s²

A. s = 2cos(7t + π/3) cm

B. s = 2cos(7t + π/2) cm

C. s = 2√2cos(7t + π/2) cm

D. s = 2√3cos(7t - π/2 cm

Lời giải:

Phương trình dao động: s = S₀cos(ωt + φ)

Tần số góc:

Từ

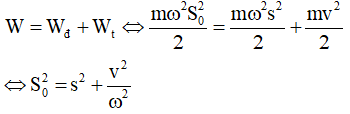
Với s = αl, v = 14 cm/s ⇒ S₀ = 2√2 cm.

Tại thời điểm t = 0 lúc con lắc qua vị trí cân bằng lần thứ nhất nên s = 0, v < 0:

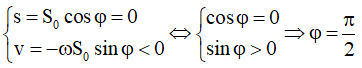
Vậy phương trình dao động của con lắc là: s = 2√2cos(7t + π/2) cm. Chọn C

Câu 5. Một con lắc đơn đang nằm yên tại vị trí cân bằng, truyền cho nó một vận tốc v₀ = 40 cm/s theo phương ngang thì con lắc đơn dao động điều hòa. Biết rằng tại vị trí có li độ góc α = 0,1√3 rad thì nó có vận tốc v = 20 cm/s. Lấy g = 10 m/s². Chọn gốc thời gian là lúc truyền vận tốc cho vật, chiều dương cùng chiều với vận tốc ban đầu. Viết phương trình dao động của con lắc theo li độ dài.

A. s = 8√2cos(5t - π/2) cm

B. s = 8cos(5t + π/2) cm

C. s = 8√2cos(5t - π/2) cm

D. s = 8cos(5t - π/2) cm

Lời giải:

Ta có:

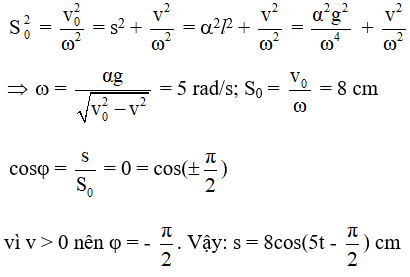
Chọn D

Câu 6. Con lắc đơn dao động điều hòa với chu kì T = π/5 s. Biết rằng ở thời điểm ban đầu con lắc ở vị trí biên, có biên độ góc α₀ với cosα₀ = 0,98. Lấy g = 10 m/s². Viết phương trình dao động của con lắc theo li độ góc.

A. α = 0,2cos10t rad.

B. α = 0,1cos10t rad.

C. α = 0,2cos(10t + π) rad.

D. α = 0,1cos(10t + π) rad.

Lời giải:

Ta có: ω = 2π/T = 10 rad/s; cosα₀ = 0,98 = cos11,48° ⇒ α₀ = 11,48° = 0,2 rad

cosφ = α/α₀ = α₀/α₀ = 1 = cos0 ⇒ = 0. Vậy α = 0,2cos10t rad. Chọn A

Câu 7. Một con lắc đơn gồm quả cầu nặng 200 g, treo vào đầu sợi dây dài l . Tại nơi có g = 9,86 m/s² con lắc dao động với biên độ nhỏ và khi qua vị trí cân bằng có vận tốc v₀ = 6,28 cm/s và khi vật nặng đi từ vị trí cân bằng đến li độ α = 0,5α₀ mất thời gian ngắn nhất là 1/6 s. Viết phương trình dao động của con lắc, biết tại t = 0 thì α = α₀ , đồng thời quả cầu đang chuyển động ra xa vị trí cân bằng. Bỏ qua ma sát và sức cản không khí.

A. s = 2cos(πt + π/3) cm

B. s = 2√2cos(πt + π/3) cm

C. s = 2cos(πt - π/3) cm

D. s = 2√2cos(πt - π/3) cm

Lời giải:

Dùng liên hệ chuyển động tròn đều và dao động điều hòa ta tính được thời gian vật nặng đi từ vị trí câng bằng đến li độ α = 0,5α₀ (hay s = 0,5S₀) mất hời gian ngắn nhất là T/12 = 1/6 ⇒ T = 2 s

Chiều dài của con lắc

Phương trình dao động của con lắc là s = S₀cos(ωt + φ)

Tần số góc: ω = π rad/s.

Vận tốc con lắc khi qua vị trí cân bằng v_max = ωS₀ = 6,28 ⇒ S₀ = 2 cm

Tại thời điểm t = 0, α = 0,5α₀ ⇒ s = 0,5S₀, quả cầu đang chuyển động ra xa vị trí cân bằng nên khi đó quả cầu đi theo chiều dương (v > 0):

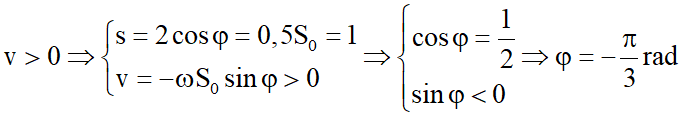
Vậy phương trình dao động của con lắc s = 2cos(πt + π/3) cm. Chọn C

Câu 8. Một con lắc đơn có chiều dài l = 40 cm , được treo tại nơi có g = 10 m/s². Bỏ qua sức cản không khí. Đưa con lắc lệch khỏi VTCB một góc 0,1 rad rồi truyền cho vật nặng vận tốc 20 cm/s theo phương vuông góc với dây hướng về VTCB. Chọn gốc tọa độ tại vị trí cân bằng của vật nặng, gốc thời gian lúc gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất. Viết phương trình dao động của con lắc theo li độ cong

A. 8cos(25t + π) cm

B. 4√2cos(25t + π) cm

C. 4√2cos(25t + π/2) cm

D. 8cos(25t) cm

Lời giải:

Phương trình dao động của con lắc theo li độ cong có dạng: s = S_maxcos(ωt + φ)

Gọi α_m là biên độ góc của dao độngn của con lắc đơn

Khi đo biên độ của tọa độ cong S_max = α_m.l → α₀ = 0,1 rad

Theo ĐL bảo toàn năng lượng ta có :

Tần số góc của dao động ω = √(g/l) = 25 rad/s

Gốc thời gian t = 0 khi gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất tức là gia tốc hướng tâm a_ht = 0 → v = 0: tức là lúc vật ở biên âm (ở điểm A).

Khi t = 0, s = -S_max → φ = π

Vậy: s = 4√2cos( ωt + π) (cm). Chọn đáp án B

Câu 9. Treo một con lắc đơn tại nơi có gia tốc g = π² m/s², chiều dài của dây treo là 1 m và bỏ qua tác dụng của lực cản. Kéo vật lệch ra khỏi vị trí cân bằng một góc 6° rồi thả nhẹ cho vật dao động điều hòa. Chọn gốc thời gian là lúc buông vật, chiều dương là chiều chuyển động của vật ngay khi buông vật. Phương trình dao động của vật nhỏ là:

A. s = (π/30)cos(πt + π) m

B. s = (π/30)cos(πt) m

C. s = 0,06cos(πt) m

D. s = 0,06cos(πt + π) m

Lời giải:

Biên độ của dao động s = l.φ = l.(π/30) = π/30 rad

Tần số góc của dao động ω = √(g/l) = π rad/s

Vậy s = (π/30)cos(πt + π) m . Chọn A

Câu 10. Con lắc đơn dao động điều hòa theo thời gian có ly độ góc mô tả theo hàm cosin với biên độ góc α₀, tần số góc ω và pha ban đầu φ. Chiều dài giây treo là l. Phương trình ly độ góc biến thiên theo thời gian có dạng

A. α = α₀cos(ωt + φ)

B. α = ωα₀cos(ωt + φ)

C. α = ω²α₀cos(ωt + φ)

D. α = lα₀cos(ωt + φ)

Lời giải:

Phương trình li độ góc biến thiên theo quy luật α = α₀cos(ωt + φ). Chọn A.

Câu 11. (Minh họa – 2017) Một con lắc đơn có chiều dài 1 m, được treo tại nơi có gia tốc trọng trường g = π² m/s². Giữ vật nhỏ của con lắc ở vị trí có li độ góc −9° rồi thả nhẹ vào lúc t = 0. Phương trình dao động của vật là

A. s = 5cos(πt + π) cm

B. s = 5cos(2πt) cm

C. s = 5πcos(πt + π) cm

D. s = 5πcos(2πt) cm

Lời giải:

Tần số góc của dao động ω = √(g/l) = √((π²)/l) = π rad/s

Biên độ cong của dao động s₀ = lα₀ = l.(9°/180°).π = 5π cm

Ban đầu vật ở vị trí biên âm, do vậy phương trình dao động sẽ là s = 5πcos(πt + π) cm. Chọn C

C. Bài tập bổ sung

Bài 1: Một con lắc đơn dao động điều hòa với biên độ góc 0,1 rad; tần số góc 10 rad/s và pha ban đầu 0,79 rad. Phương trình dao động của con lắc là

A. α = 0,1cos(20πt - 0,79)rad                      

B. α = 0,1cos(20πt + 0,79)rad

C. α = 0,1cos(10t - 0,79)rad                         

D. α = 0,1cos(10t + 0,79)rad

Bài 2: Một con lắc đơn có chu kì dao động với biên độ nhỏ là T = 2π/5. Khối lượng con lắc là m = 60g,  biên độ góc là α₀  với cosα₀ = 0,991. Lấy g = 9,8m/s². Chọn gốc tọa độ là vị trí cân bằng, chọn gốc thời gian là lúc con lắc ở vị trí biên. Phương trình nào là phương trình dao động của con lắc.

A. α = 0,18cos(5πt - π/6) (rad).                    

B. α = 0,134cos5t (cm)(rad)

C. α = 0,18cos(5t - π/6) (rad)                     

D. α = 0,134cos(5t - π/6) (rad)

Bài 3: Quả cầu của con lắc đơn có khối lượng m = 60g khi dao động vạch ra một cung tròn coi như một đoạn thẳng dài 12cm. Dây treo con lắc dài l = 1,2m; g = 9,8m/s² . Chọn gốc tọa độ là vị trí cân bằng, chọn gốc thời gian là lúc vật qua vị trí cân bằng theo chiều dương. Phương trình dao động của con lắc đơn là:

A. s = 12cos(2,2t - π/2) (cm)

B. s = 12cos(2,86t) (cm)

C. s = 6cos(2,2t + π/2) (cm)

D. s = 6cos(2,86t - π/2) (cm)

Bài 4: Một con lắc đơn, vật năng có khối lượng m = 100g, chiều dài dây treo là 1m, g= 9,86m/s² . Bỏ qua mọi ma sát. Kéo con lắc lệch khỏi vị trí cân bằng góc α₀ rồi thả không vận tốc đầu. Biết con lắc dao động điều hòa với năng lượng E = 8.10^-4J. Lập phương trình dao động điều hòa của con lắc, chọn gốc thời gian là lúc vật có li độ cực đại dương.

A. s = 4cos(πt) (cm)                                                

B. s = 16cos(πt - π/3) (cm) 

C. s = 4cos(πt - π) (cm)                               

D. s = 16cos(πt - 2π/3) (cm)

Bài 5: Một con lắc đơn dao động ở nơi có g = 10m/s², π² = 10, l = 0,8 m, A = 12cm. Chọn gốc tọa độ tại vị trí cân bằng, t = 0 lúc vật qua vị trí cân bằng theo chiều dương. Phưong trình dao động của vật là

A. s = 12cos(5√2t)                                       

B. s = 12cos(2,5√2t - π/2) 

C. s = 12cos(2,5√2t + π/2)

D. s = 24cos(2,5√2t)

Bài 6: Lò xo có chiều dài tự nhiên là l₀ = 25 cm treo tại một điểm cố định, đầu dưới mang vật nặng 100 g. Từ vị trí cân bằng nâng vật lên theo phương thẳng đứng đến lúc chiều dài của lò xo là 31 cm rồi buông ra. Quả cầu dao động điều hòa với chu kỳ T = 0,628 s, chọn gốc toạ độ tại vị trí cân bằng, chiều dương hướng xuống. Tại thời điểm t = π/30skể từ lúc bắt đầu dao động vật đi qua vị trí cân bằng theo chiều âm. Phương trình dao động của vật là

A. x = 6cos(10t + π/6)(cm).                         

B. x = 6cos(10t - π/6)(cm).

C. x = 4cos(10t - π/6)(cm).                         

D. x = 4cos(10t + π/6)(cm).

Bài 7: Một con lắc lò xo gồm quả cầu nhỏ có khối lượng 500g và lò xo có độ cứng k đang dao động điều hòa, cơ năng của con lắc bằng 0,01(J), tại thời điểm t₁ = π√3/60 (s) (kể từ lúc t =0 ) thì vật có vận tốc 0,1 (m/s) và gia tốc -1 (m/s²) thì phương trình dao động của quả cầu là:

A. $x=2\sqrt{3}\cos \left(\frac{10}{\sqrt{3}}t+\frac{\mathrm{\pi }}{3}\right)$ (cm).                  

B. $x=4\sqrt{3}\cos \left(\frac{20}{\sqrt{3}}t+\frac{\mathrm{\pi }}{6}\right)$(cm).

C. $x=2\sqrt{3}\cos \left(\frac{20}{\sqrt{3}}t-\frac{\mathrm{\pi }}{6}\right)$ (cm).                            

D. $x=2\sqrt{3}\cos \left(\frac{10}{\sqrt{3}}t-\frac{\mathrm{\pi }}{3}\right)$(cm).

Bài 8: Một con lắc lò xo dao động không ma sát trên mặt phẳng ngang, biết rằng trong quá trình dao động quãng đường đi lớn nhất trong khoảng thời gian Δt < T/2 là 20cm và quãng đường đi nhỏ nhất trong khoảng thời gian Δt là (40 - 20√3)cm, tại thời điểm t₁ = 0,5s thì vật đang có động năng bằng 3 thế năng và đang chuyển động chậm theo chiều âm, tại thời điểm t₂ = 1s gần t₁ nhất  vật đang có động năng bằng cơ năng. Viết phương trình dao động con lắc lò xo

A. $\mathrm{x}=40\cos \left(\frac{10\mathrm{\pi t}}{3}-\frac{\mathrm{\pi }}{6}\right)\left(\mathrm{cm}\right)$.                                         

B. $\mathrm{x}=20\cos \left(\frac{5\mathrm{\pi t}}{3}+\frac{\mathrm{\pi }}{6}\right)\left(\mathrm{cm}\right)$ .

C. $\mathrm{x}=40\cos \left(\frac{10\mathrm{\pi t}}{3}+\frac{\mathrm{\pi }}{6}\right)\left(\mathrm{cm}\right)$                       

D. $\mathrm{x}=20\cos \left(\frac{5\mathrm{\pi t}}{3}-\frac{\mathrm{\pi }}{6}\right)\left(\mathrm{cm}\right)$ .

Bài 9: Một con lắc lò xo gồm quả cầu nhỏ và lò xo có độ cứng k = 80N/m. Con lắc thực hiện 100 dao động hết 31,4s. Chọn gốc thời gian là lúc quả cầu có li độ 2cm và đang chuyển động theo chiều dương của trục tọa độ với vận tốc có độ lớn 40√3 cm/s thì phương trình dao động của quả cầu là

A. x = 4cos(20t - π/3)(cm).                                 

B. x = 6cos(20t + π/6)(cm).

C. x = 4cos(20t + π/6)(cm).                               

D. x = 6cos(20t - π/6)(cm).

Bài 10: Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng k = 100 N/m, vật có khối lượng m = 1 kg. Kéo vật dọc theo trục của lò xo xuống dưới vị trí cân bằng 3 cm và truyền cho nó vận tốc 30 cm/s hướng lên. Chọn gốc tọa độ tại vị trí cân bằng của vật, chiều dương hướng xuống, gốc thời gian là lúc vật được truyền vận tốc. Phương trình dao động của vật là

A. x = 3cos(10t + π/4)(cm).                                     

B. x = 3√2cos(10t + π/4)(cm).

C. x = 3cos(10t - π/4)(cm).                        

D. x = 3√2cos(10t - π/4)(cm).

Xem thêm các dạng bài tập Vật Lí lớp 12 ôn thi Tốt nghiệp có lời giải hay khác:

• Dạng 1: Viết phương trình dao động của Con lắc đơn

• Dạng 2: Chu kì con lắc đơn thay đổi

• Dạng 3: Con lắc trùng phùng

• Dạng 4: Năng lượng con lắc đơn và lực căng dây

• Bài tập con lắc đơn (Phần 1)

• Bài tập con lắc đơn (Phần 2)

• Bài tập con lắc đơn (Phần 3)

---

---

---