Cách xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng (hay, chi tiết)
Bài viết Cách xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Cách xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng.
- Cách giải xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng
- Ví dụ minh hoạ xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng
- Bài tập vận dụng xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng
- Bài tập bổ sung xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng
Cách xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng (hay, chi tiết)
(199k) Xem Khóa học Vật Lí 12 KNTTXem Khóa học Vật Lí 12 CDXem Khóa học Vật Lí 12 CTST
A. Phương pháp giải
1. Điều kiện cho điểm cực đại dao động cùng pha, ngược pha với hai nguồn đồng pha.
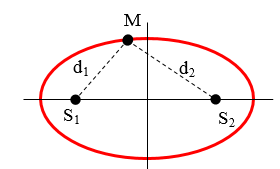
+ Phương trình sóng tại 2 nguồn cùng biên độ A: (Điểm M cách hai nguồn lần lượt d1, d2)
u1 = Acos(2πft +φ) và u2 = Acos(2πft +φ)
+ Phương trình giao thoa sóng tại M:
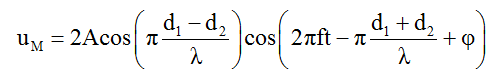
+ Điều kiện để M dao động cực đại và đồng pha với hai nguồn:
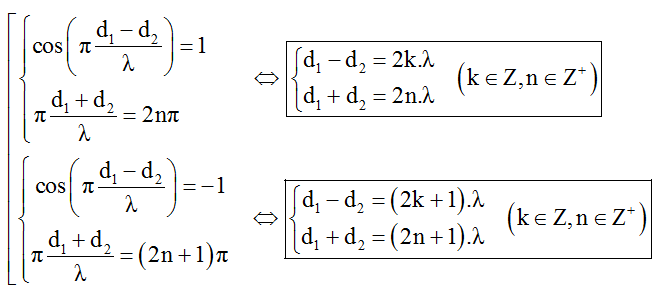
+ Điều kiện để M dao động cực đại và ngược pha với hai nguồn:
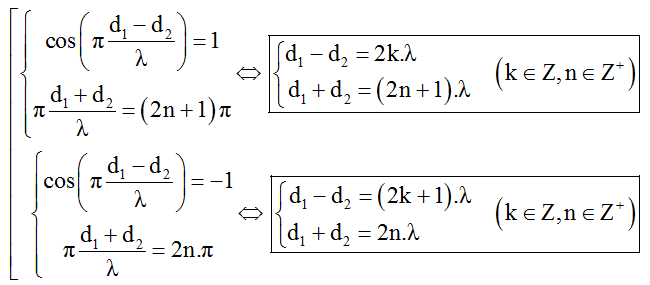
* Tổng quát hóa:
+ Điều kiện để M dao động với biên độ cực đại và cùng pha với nguồn là:
- Cực đại: d1 – d2 = k.λ.
- Cùng pha: d1 + d2 = n.λ
Với k và n hoặc cùng chẵn hoặc cùng lẻ.
+ Điều kiện để M dao động với biên độ cực đại và ngược pha với nguồn là:
- Cực đại: d1 – d2 = k.λ.
- Cùng pha: d1 + d2 = n.λ
Với k, n là chẵn lẻ (k lẻ thì n chẵn hoặc ngược lại).
2. Khoảng cách gần nhất từ điểm cực đại đồng pha, ngược pha với nguồn tới đoạn nối 2 nguồn và đường trung trực của hai nguồn.
* Xét bài toán có điểm M dao động cực đại và đồng pha với nguồn.
a) Xác định điểm M gần nhất với nguồn S1 (hoặc tới đoạn thẳng nối 2 nguồn) khi 2 nguồn cùng pha.
Bước 1: Xác định số vân cực đại trên đoạn nối 2 nguồn qua bất phương trình tìm k ϵ Z sau:
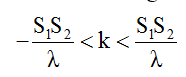
Suy ra cực đại ngoài cùng có k có độ lớn bằng |kn| = [S1S2/λ]
Bước 2: Viết điều kiện để điểm M cực đại và đồng pha với hai nguồn.
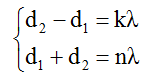
với n, k cùng chẵn hoặc cùng lẻ.
Vì M gần nguồn S1 nhất (hoặc gần S1S2 nhất) nên M thuộc cực đại ngoài cùng.
Suy ra k = kn. Do đó nếu kn lẻ thì n phải lẻ hoặc nếu kn chẵn thì n chẵn.
Bước 3: Xác định d1 và d2:
+ Tìm giá trị của n qua bất đẳng thức tam giác: d1 + d2 > S1S2
⇔ n > S1S2/λ. Tùy theo n chẵn hay lẻ, ta chọn giá trị nguyên nhỏ nhất n = nmin.
+ Giải hệ phương trình:
Ta tìm được d1; d2. Suy ra MS1min = d1.
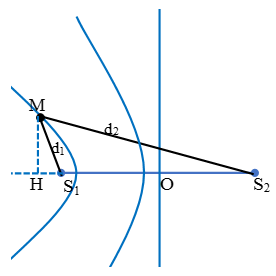
Bước 4: Tìm khoảng cách từ M đến S1S2.
Dựa vào định lý hàm số cos trong ∆MS1S2 ta xác định góc :
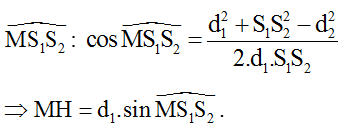
b) Xác định điểm M gần nhất với đường trung trực của hai nguồn khi 2 nguồn cùng pha.
+ M dao động cực đại gần đường trung trực của S1S2 nhất khi M thuộc cực đại bậc 1.
Do đó M cần tìm có điều kiện: 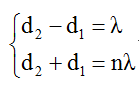
+ Tìm giá trị của n qua bất đẳng thức tam giác: d1 + d2 > S1S2
⇔ n > S1S2/λ . Ta chọn giá trị nguyên lẻ nhỏ nhất n = nmin.
+ Giải hệ phương trình: ta tìm được d1; d2.
Từ hình vẽ: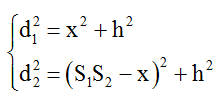
Vậy khoảng cách giữa M và ∆ khi đó bằng HO = OS1 –S1H = 0,5S1S2 – x.
* Xét bài toán có điểm M dao động cực đại và ngược pha với nguồn.
Ta làm tương tự như trường hợp trên với điều kiện cho điểm M cực đại ngược pha với hai nguồn là: 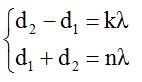
B. Ví dụ minh họa
Ví dụ 1: (THPTQG – 2017): Ở mặt nước, tại hai điểm S1 và S2 có hai nguồn kết hợp, dao động điều hòa, cùng pha theo phương thẳng đứng. Biết sóng truyền trên mặt nước với bước sóng λ, khoảng cách S1S2 = 5,6λ. Ở mặt nước, gọi M là vị trí mà phần tử nước tại đó dao động với biên độ cực đại, cùng pha với dao động của hai nguồn. Khoảng cách ngắn nhất từ M đến đường thẳng S1S2 là
A. 0,868λ. B. 0,852λ. C. 0,754λ. D. 0,946λ.
Hướng dẫn giải:
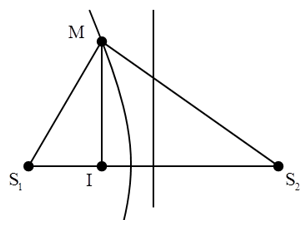
Chọn C.
+ Điểm M dao động cực đại, cùng pha với nguồn khi:
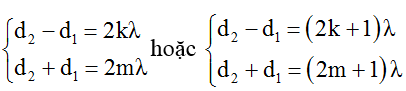
→ d1 = (m – k)λ
Do đó M gần S1S2 nhất khi d1min = λ khi (m – k)min = 1
+ Mặt khác d2 + d1 > S1S2 = 5,6λ
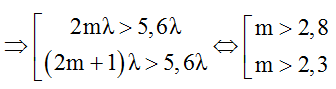
→ mmin= 3 → kmin = 2 (M nằm trên đường cực đại bậc 2)
=> d1min = λ; d2min = 5λ
Từ hình học ta có:
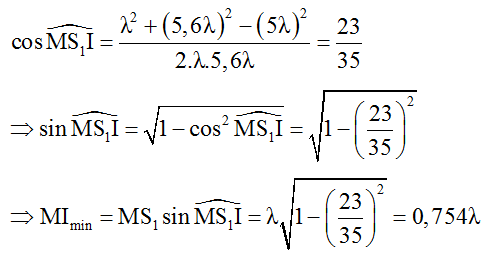
C. Bài tập vận dụng
Câu 1: Ở mặt thoáng của chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình uA = uB = a.cos(20πt) (t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A. Khoảng cách AM là
A. 2,5 cm B. 2 cm C. 5 cm D. 1,25 cm
Lời giải:
Chọn C.
Bước sóng: λ = v/f = 50/10 = 5cm.
Áp dụng kết quả bài toán điều kiện để một vị trí cực đại và cùng pha với nguồn:

→ d1 = (m – k)λ
Do đó d1min khi (m – k)min = 1 → d1min = λ = 5cm.
Câu 2: Tại hai điểm A, B trên mặt nước cách nhau 16 cm có hai nguồn phát sóng giống nhau. Điểm M nằm trên mặt nước và trên đường trung trực của AB cách trung điểm I của AB một khoảng nhỏ nhất bằng 4√5 cm luôn dao động cùng pha với I. Điểm N nằm trên mặt nước và nằm trên đường thẳng vuông góc với AB tại A, cách A một khoảng nhỏ nhất bằng bao nhiêu để N dao động với biên độ cực tiểu.
A. 9,22 cm B. 8,75 cm C. 2,14 cm D. 8,57 cm.
Lời giải:
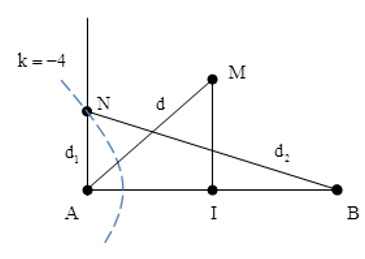
Chọn C.
Vì hai nguồn đồng pha, M, I đều thuộc trung trực của AB nên để M và I dao động cùng pha thì: MA – IA = k.λ
M gần I nhất nên k = 1→ MA = dA = 0,5AB + λ = 8 + λ.
Mặc khác MI = 4√5 cm
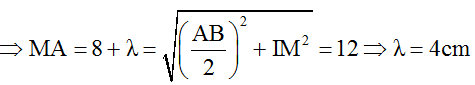
Số điểm dao động với biên độ cực tiểu trên AB:
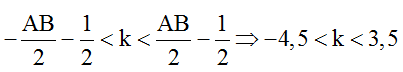
Để N là một điểm cực tiểu và gần A nhất thì N phải nằm trên hypebol cực tiểu có k = -4
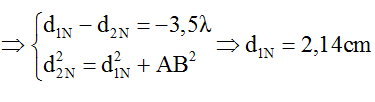
Câu 3: Tại mặt chất lỏng, hai nguồn S1, S2 cách nhau 13 cm dao động theo phương thẳng đứng với phương trình u1 = u2 = Acos(40πt) (cm) (t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 80 cm/s. Ở mặt chất lỏng, gọi ∆ là đường trung trực của S1S2. M là một điểm không nằm trên S1S2 và không thuộc ∆, sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với hai nguồn. Khoảng cách ngắn nhất từ M đến ∆ là
A. 2,00 cm. B. 2,46 cm. C. 3,07 cm. D. 4,92 cm.
Lời giải:
Chọn C.
+ Điều kiện để M dao động cực đại và đồng pha với hai nguồn là:
với n, k cùng chẵn hoặc cùng lẻ.
+ Để M gần ∆ nhất thì k = 1, n khi đó có thể nhận các giá trị lẻ 1, 3…..thỏa mãn bất đẳng thức tam giác:
d1 + d2 > S1S2 = 13 => n > 13/λ = 3,25 => nmin = 5 (do n lẻ).
+ Ta có:
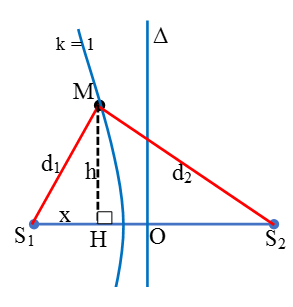
+ Từ hình vẽ:
Vậy khoảng cách giữa M và ∆ khi đó bằng HO = OS1 –S1H = 13/2 – 3,42 = 3,07cm.
Câu 4: (THPTQG 2018). Ở mặt nước có hai nguồn kết hợp đặt tại hai điểm A và B, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng λ. Trên AB có 9 vị trí mà ở đó các phần tử nước dao động với biên độ cực đại. C và D là hai điểm ở mặt nước sao cho ABCD là hình vuông. M là một điểm thuộc cạnh CD và nằm trên vân cực đại giao thoa bậc nhất (MA – MB = λ). Biết phần tử tại M dao động ngược pha với các nguồn. Độ dài đoạn AB gần nhất với giá trị nào sau đây?
A. 4,3 λ B. 4,7 λ C. 4,6 λ D. 4,4 λ
Lời giải:
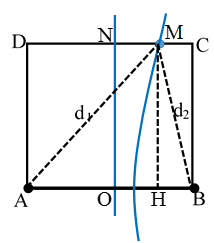
Chọn D.
Đặt AB = a. Hai nguồn đồng pha và trên đoạn AB có 9 cực đại nên 4λ ≤ AB = a < 5λ.
Ta có: AN = NB = √5/2 AB => 2√5λ < AN < 5√5/2λ .
Vì M là cực đại và ngược pha với nguồn nên ta có:
với k, m ϵ Z và k lẻ, n chẵn hoặc k chẵn thì n lẻ.
M là cực đại bậc 1 nên k = 1 → m là số dương chẵn.
Từ hệ trên ta suy ra
Từ hình học, ta được:
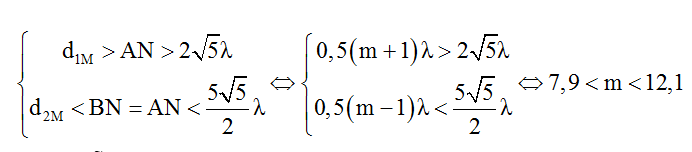
Vì m chẵn nên m = 8; 10 hoặc 12. Ta có bảng giá trị sau:
| m | 8 | 10 | 12 |
| d1M | 4,5λ | 5,5λ | 6,5λ |
| d2M | 3,5 λ | 4,5λ | 5,5λ |
Ta có:
TH1: d1 = 4,5λ; d2 = 3,5λ → a = 3,453λ (loại)
TH2: d1 = 5,5λ; d2 = 4,5λ → a = 4,376λ (thỏa mãn)
TH3: d1 = 6,5λ; d2 = 5,5λ → a = 5,289λ (loại)
Vậy AB = 4,376λ.
Câu 5: Ở mặt chất lỏng có hai nguồn sóng S1, S2 cách nhau 19 cm, dao động theo phương thẳng đứng với phương trình là u1 = u2 = acos20πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 40 cm/s. Gọi M là điểm ở mặt chất lỏng, gần A nhất sao cho phần từ chất lỏng tại M dao động với biên độ cực đại và cùng pha với các nguồn. Khoảng cách từ M tới AB là
A. 2,86 cm B. 3,96 cm C. 1,49 cm D. 3,18 cm.
Lời giải:
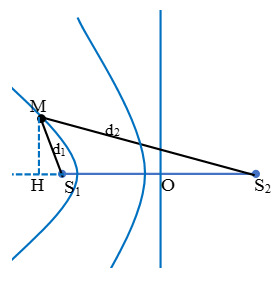
Chọn B.
Bước sóng λ = v/f = 40/10 = 4cm.
Số điểm dao động với biên độ cực đại trên S1S2:
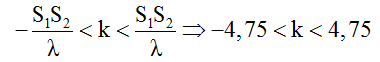
Điều kiện để M dao động cực đại và đồng pha với hai nguồn là:
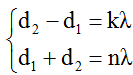
với n, k cùng chẵn hoặc cùng lẻ.
Do đó M gần S1 nhất nên M thuộc cực đại ngoài cùng (M nằm trên cực đại bậc 4)
Suy ra k = 4 và n phải chẵn.
Mặt khác d2 + d1 > S1S2 = 19cm → n.λ > 19 ↔ n > 4,75.
Vì n chẵn nên nmin = 6.
+ Khi đó ta có:
Từ hình học ta có:
Vậy
D. Bài tập bổ sung
Câu 1: Trên mặt thoáng của một chất lỏng có hai nguồn kết hợp ngược pha A và B cách nhau 10cm. Tần số hai sóng là 20Hz, vận tốc truyền sóng trên mặt chất lỏng là 30cm/s. Số điểm dao động với biên độ cực đại trên AB.
A. 16
B. 13
C. 14
D. 15
Câu 2: Ở mặt nước, tại hai điểm A và B có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. ABCD là hình vuông nằm ngang. Biết trên AB có 15 vị trí mà ở đó các phần tử dao động với biên độ cực đại. Số vị trí trên CD tối đa ở đó dao động với biên độ cực đại là
A. 7
B. 5
C. 3
D. 9
Câu 3: Tại A và B cách nhau 9cm có hai nguồn sóng cơ kết hợp có cùng tần số f = 50Hz, vận tốc truyền sóng v = 1m/s. Số gợn cực đại đi qua đoạn AB là:
A. 7
B. 5
C. 11
D. 9
Câu 4: Hai nguồn kết hợp A, B trên mặt nước cách nhau một đoạn AB = 7λ (λ là bước sóng) dao động với phương trình uA = ub = cosωt. Trên đoạn AB, số điểm có biên độ cực đại và ngược pha với hai nguồn (không kể hai nguồn) là
A. 8
B. 7
C. 10
D. 14
Câu 5: Cách 2 điểm A, B cách nhau 13cm trên mặt nước có 2 nguồn sóng đồng bộ, tạo ra sóng mặt nước có bước sóng là 1,2 cm. M là điểm trên mặt nước cách A và B lần lượt là 12 cm và 5 cm. N đối xứng với M qua AB. Số hyperbol cực đại cắt đoạn MN là:
A. 0
B. 3
C. 2
D. 4
Câu 6: Trong thí nghiệm giao thoa sóng nước, hai viên bi nhỏ S1 và S2 gắn ở cần rung cách nhau 2cm và chạm nhẹ vào mặt nước. Khi cần rung dao động theo phương thẳng đứng với tần số f = 100 Hz thì tạo ra sóng truyền trên mặt nước với vận tốc v = 60 cm/s. Một điểm M nằm trong miền giao thoa và cách S1, S2 các khoảng d1 = 2,4 cm; d2 = 1,2 cm. Xác định số điểm dao động với biên độ cực đại trên đoạn MS1.
A. 7
B. 5
C. 6
D. 8
Câu 7: Hai nguồn sóng A, B cách nhau 12,5 cm trên mặt nước giao thoa sóng, dao động tại nguồn có phương trình uA = uB = acos100πt (cm) tốc độ truyền sóng trên mặt nước là 0,5 m/s. Số điểm trên đoạn AB dao động với biên độ cực đại và dao động ngược pha với trung điểm I của đoạn AB là:
A. 20
B. 13
C. 12
D. 24
Câu 8: Tại hai điểm A, B cách nhau 13 cm trên mặt nước có hai nguồn phát sóng giống nhau. Cùng dao động theo phương trình uA = uB = acosωt (cm). Sóng truyền đi trên mặt nước có bước sóng là 2 cm, coi biên độ sóng không đổi khi truyền đi. Xét điểm M trên mặt nước thuộc đường thẳng By vuông góc với AB và cách A một khoảng 20 cm. Trên By, điểm dao động với biên độ cực đại cách M một khoảng nhỏ nhất bằng.
A. 3,14 cm
B. 2,33 cm
C. 2,93 cm
D. 4,11 cm
Câu 9: Tại hai điểm A và B trên mặt nước cách nhau 8cm có hai nguồn kết hợp dao động với phương trình: u1 = u2 = acos40πt cm, tốc độ truyền sóng trên mặt nước là 30cm/s. Xét đoạn thảng CD = 4cm trên mặt nước có chung đường trung trực với AB. Khoảng cách lớn nhất từ CD đến AB sao cho trên đoạn CD chỉ có 3 điểm dao động với biên độ cực đại là
A. 3,3 cm
B. 8,9 cm
C. 6 cm
D. 9,7 cm
Câu 10: Trong một thí nghiệm giao thoa sóng nước, hai nguồn sóng kết hợp cùng pha đặt tại hai điểm A và B cách nhau 16 cm. Sóng truyền trên mặt nước có bước ongs 3cm. Gọi là một đường thẳng nằm trên mặt nước, qua A và vuông góc với AB. Coi biên độ sóng trong quá trình lan truyền không đổi. Số điểm dao động với biên độ cực đại nằm trên là:
A. 22
B. 10
C. 12
D. 20
(199k) Xem Khóa học Vật Lí 12 KNTTXem Khóa học Vật Lí 12 CDXem Khóa học Vật Lí 12 CTST
Xem thêm các dạng bài tập Vật Lí lớp 12 ôn thi Tốt nghiệp có lời giải hay khác:
- Xác định biên độ, li độ, vận tốc, gia tốc trong miền giao thoa sóng
- Tìm số điểm dao động cực đại, cực tiểu giữa hai nguồn, hai điểm bất kì trong giao thoa sóng
- Bài toán về điểm cực đại, cực tiểu gần nhất, xa nhất với nguồn trong giao thoa sóng
- Xác định vị trí, số điểm dao động cùng pha, ngược pha với nguồn trong giao thoa sóng
- Bài tập giao thoa sóng cơ nâng cao, hay và khó, có lời giải
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

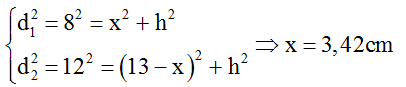
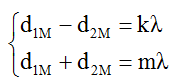
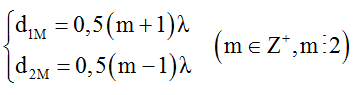
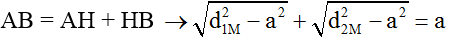
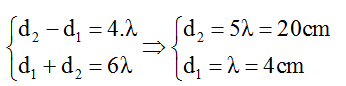
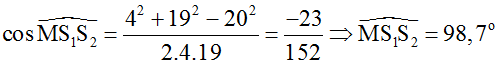
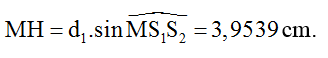



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

