Cho tam giác ABC. Gọi D là trung điểm của AB

Giải vở thực hành Toán 7 Bài tập ôn tập cuối năm

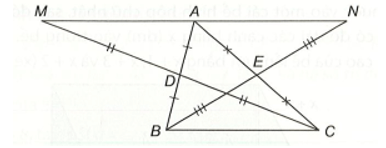
Bài 8 trang 107 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho DM = DC.

a) Chứng minh rằng ∆ADM = ∆BDC. Từ đó suy ra AM = BC và AM // BC.

b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng AN // BC.

c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.

Lời giải:

a) ∆ADM và ∆BDC có

AD = DB (do D là trung điểm của AB)

$\widehat{A\text{D}M}=\widehat{B\text{D}C}$ (hai góc đối đỉnh)

DM = DC (giả thiết)

Nên ∆ADM = ∆BDC (c.g.c).

Suy ra AM = BC (hai cạnh tương ứng) và $\widehat{MAD}=\widehat{CBD}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AM // BC (dấu hiệu nhận biết hai đường thẳng song song).

b) ∆AEN và ∆CEB có:

AE = CE (E là trung điểm của AC)

$\widehat{A\text{E}N}=\widehat{CEB}$ (hai góc đối đỉnh)

EN = EB (theo giả thiết)

Nên ∆AEN = ∆CEB (c.g.c).

Suy ra $\widehat{E\text{A}N}=\widehat{ECB}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AN // BC (dấu hiệu nhận biết hai đường thẳng song song).

c) Ta có AM // BC (chứng minh trên),

   AN // BC (chứng minh trên) nên AM và AN trùng nhau (theo tiên đề Euclid).

Từ đó suy ra ba điểm M, A, N thẳng hàng.

Ta lại có AM = BC (chứng minh trên), AN = BC (chứng minh trên – do ∆AEN = ∆CEB),

do đó AM = AN.

Từ đó suy ra A là trung điểm của đoạn MN.

Xem thêm các bài giải vở thực hành Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

• Bài 1 trang 104 vở thực hành Toán lớp 7 Tập 2: Tính giá trị của các biểu thức sau:$\sqrt{25}$ + (2² . 3)² . ${\left(-\frac{1}{4}\right)}^2$ + 2020⁰ + $\left|-\frac{1}{4}\right|$;...
• Bài 2 trang 104 vở thực hành Toán lớp 7 Tập 2: Tính một cách hợp lí.$\frac{5}{11}-\frac{10}{19}+1,5+\frac{17}{11}-\frac{9}{19}$;...
• Bài 3 trang 104 vở thực hành Toán lớp 7 Tập 2: a) Tìm x, biết $\frac{2}{5}$x + $\frac{3}{2}$= $\frac{3}{5}-\left(-\frac{1}{4}\right)$....
• Bài 4 trang 105 vở thực hành Toán lớp 7 Tập 2: Hai người thợ cùng làm tổng cộng được 136 sản phẩm (thời gian làm như nhau). Hỏi mỗi người thợ làm được bao nhiêu sản phẩm, biết rằng người thợ thứ nhất làm một sản phẩm mất 9 phút, còn người thứ hai làm mất 8 phút?...
• Bài 5 trang 105 vở thực hành Toán lớp 7 Tập 2: Ba khối 6, 7, 8 của một trường Trung học cơ sở tham gia quyên góp vở tặng các bạn vùng khó khăn. Biết rằng số vở quyên góp được của ba khối theo thứ tự tỉ lệ thuận với 8, 7, 6 và số vở khối 8 quyên góp được ít hơn số vở khối 6 quyên góp được là 80 quyển..
• Bài 6 trang 105 vở thực hành Toán lớp 7 Tập 2: Cho hai đa thức A = 6x³ - 4x² - 12x - 7 và B = 2x² - 7....
• Bài 7 trang 107 vở thực hành Toán lớp 7 Tập 2: Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng x (dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng x + 1, x + 3 và x + 2 (xem dưới đây)....
• Bài 9 trang 108 vở thực hành Toán lớp 7 Tập 2: Cho tam giác cân ABC tại đỉnh A. Gọi H là trung điểm của BC....
• Bài 10 trang 110 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho BD = BA và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:...
• Bài 11 trang 111 vở thực hành Toán lớp 7 Tập 2: Bình thu thập số liệu về số học sinh phổ thông của cả nước từ năm 2015 đến năm 2020 và vẽ được biểu đồ dưới đây:...
• Bài 12 trang 112 vở thực hành Toán lớp 7 Tập 2: Biểu đồ nào sau đây cho biết tổng số huy chương thế giới mà thể thao Việt Nam giành được trong các năm từ 2015 đến 2019:...
• Bài 13 trang 113 vở thực hành Toán lớp 7 Tập 2: Trong trò chơi Vòng quay may mắn, người chơi sẽ quay một bánh xe hình tròn. Bánh xe được chia làm 12 hình quạt bằng nhau như hình bên. ...

---