Bài 2.5 trang 33 Chuyên đề Toán 12 Kết nối tri thức
Giải Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính - Kết nối tri thức
Bài 2.5 trang 33 Chuyên đề Toán 12: Một hãng bán gà rán nghiên cứu thấy rằng để làm ra món gà rán có chất lượng tốt nhất thì thức ăn cho gà cần được bổ sung thêm 4 loại vitamin V1, V2, V3 và V4. Tổng lượng vitamin tối thiểu phải bổ sung cho mỗi 100 gam thức ăn cho gà là: V1 cần 50 đơn vị, V2 cần 100 đơn vị, V3 cần 60 đơn vị và V4 cần 180 đơn vị. Có hai loại thức ăn S1 và S2 cung cấp 4 loại vitamin này. Loại S1 có giá 720 đồng một gam và mỗi gam S1 có chứa 5 đơn vị V1, 25 đơn vị V2, 10 đơn vị V3 và 35 đơn vị V4. Loại S2 có giá 960 đồng một gam và mỗi gam S2 có chứa 25 đơn vị V1, 10 đơn vị V2, 10 đơn vị V3 và 20 đơn vị V4. Hỏi cần phải thêm vào 100 gam thức ăn cho gà mỗi loại S1 và S2 bao nhiêu gam để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà?
Lời giải:
Gọi x, y lần lượt là số gam thức ăn loại S1 và S2 cần thêm vào 100 gam thức ăn cho gà.
Chi phí mua thức ăn là: F(x; y) = 720x + 960y (đồng).
Hệ bất phương trình ràng buộc x và y là
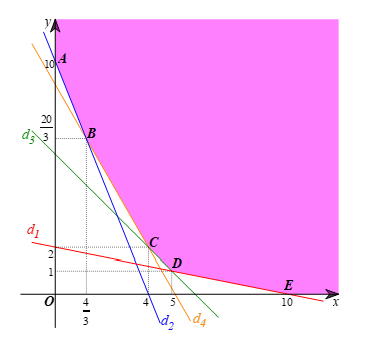
Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
Ở đây, d1: x + 5y = 10, d2: 5x + 2y = 20, d3: x + y = 6 và d4: 7x + 4y = 36.
Các điểm cực biên là: A(0; 10), C(4; 2), D(5; 1), E(10; 0).
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Tính giá trị của F(x; y) tại các điểm cực biên ta được:
F(0; 10) = 720.0 + 960.10 = 9 600;
F(4; 2) = 720.4 + 960.2 = 4 800;
F(5; 1) = 720.5 + 960.1 = 4 560;
F(10; 0) = 720.10 + 960.0 = 7 200.
Do đó giá trị nhỏ nhất của F(x; y) bằng 4 560 tại điểm cực biên D(5; 1).
Vậy cần phải thêm vào 100 gam thức ăn cho gà là 5 g loại S1 và 1 g loại S2 để chi phí là thấp nhất mà vẫn đảm bảo dinh dưỡng cho gà.
Lời giải bài tập Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác:
Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Kết nối tri thức hay, chi tiết khác:
Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu
Chuyên đề Toán 12 Bài 7: Đầu tư tài chính. Lập kế hoạch tài chính cá nhân
Xem thêm các tài liệu học tốt lớp 12 hay khác:
- Giải Chuyên đề học tập Toán 12 Kết nối tri thức
- Giải Chuyên đề học tập Toán 12 Chân trời sáng tạo
- Giải Chuyên đề học tập Toán 12 Cánh diều
- Giải lớp 12 Kết nối tri thức (các môn học)
- Giải lớp 12 Chân trời sáng tạo (các môn học)
- Giải lớp 12 Cánh diều (các môn học)
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

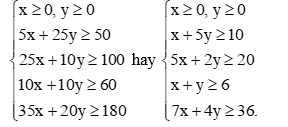



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

