Giải Toán 8 VNEN Bài 8: Ứng dụng thực tế của tam giác đồng dạng

A.B. Hoạt động khởi động và hình thành kiến thức

1 (Trang 76 Toán 8 VNEN Tập 2)

Em suy nghĩ

- Có thể đo chiều cao của một tòa nhà, của một ngọn tháp hay của một nào đó mà không cần lên đến đỉnh?

Trả lời: Có thể

- Đo khoảng cách giữa hai điểm trong đó có một điểm không thể tới được?

Trả lời: Có thể

C. Hoạt động luyện tập

1 (Trang 78 Toán 8 VNEN Tập 2)

Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m va đặt cây xa 18m. Sau khi người ấy lùi ra xa cách cọc 1m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thằng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5m?

Lời giải:

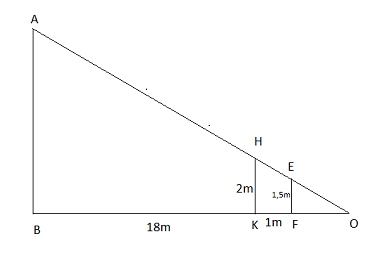
Gọi các điểm như hình vẽ, khi đó chiều cao cây chính là độ dài đoạn thẳng AB.

Ta có: Δ OEF Δ OHK nên 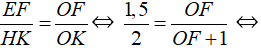OF = 3m.

Δ OEF Δ OAB nên 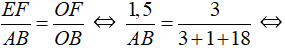AB = 11m

Vậy cây cao 11m.

2 (Trang 78 Toán 8 VNEN Tập 2)

Để đo khoảng cách giữa hai địa điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính cách khoảng cách AB như hình 51: AB // DF; AD = m; DC = n, DF = a.

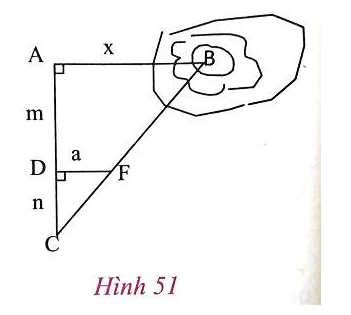
a) Em hãy nói rõ cách đo như thế nào.

b) Tính độ dài x của khoảng cách AB.

Lời giải:

a) Cách đo:

Chọn hai điểm C và D sao cho A, D, C thẳng hàng AC ⊥ AB

Chọn điểm C ∈ AD và điểm F sao cho cho C, F, B thẳng hàng và DF ⊥ AD

b) Ta có: Δ DFC ∼ Δ ABC nên:

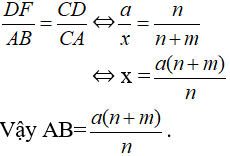
3 (Trang 78 Toán 8 VNEN Tập 2)

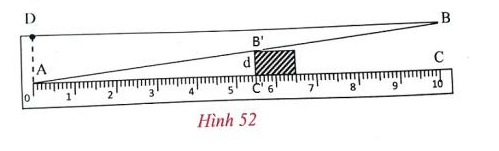
Hình 52 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm.

Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại va thước (đáy của vật áp vào bề mặt của thước A

C). Khi đó, trên thước AC ta được "bể dày" d của vật (trên hình vẽ ta có d = 5,5mm).

Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi các vạch trên thước AC (d ≤ 10mm).

Lời giải:

Theo hình vẽ thì ∆ABC ∽ ∆A'B'C' nên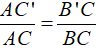

Vì B'C' là bề dầy cần đo =>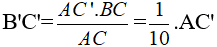

Vậy khi đọc AC' = 5,5 cm thì được B'C' = 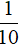. 5,5 cm = 5,5 mm

Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì cạnh tương ứng tỉ lệ

Xem thêm các bài Giải bài tập Toán lớp 8 chương trình VNEN hay khác:

• Bài 4: Khái niệm hai tam giác đồng dạng
• Bài 5: Trường hợp đồng dạng thứ nhất
• Bài 6: Trường hợp đồng dạng thứ hai
• Bài 7: Trường hợp đồng dạng thứ ba
• Bài 9: Ôn tập chương III

ĐỀ THI, GIÁO ÁN, SÁCH LUYỆN THI DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 8

Bộ giáo án, bài giảng powerpoint, đề thi, sách dành cho giáo viên và gia sư dành cho phụ huynh tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

Tổng đài hỗ trợ đăng ký : 084 283 45 85

Giáo án, bài giảng powerpoint Văn, Toán, Lí, Hóa....

4.5 (243)

799,000đs

199,000 VNĐ

Đề thi, chuyên đề Cánh diều, Kết nối tri thức, Chân trời sáng tạo...

4.5 (243)

799,000đ

99,000 VNĐ

Sách Toán - Văn- Anh 6-7-8-9, luyện thi vào 10

4.5 (243)

199,000đ

99.000 - 149.000 VNĐ

xem tất cả

Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.

Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:

Loạt bài Giải bài tập Toán 8 (sgk, sbt, vbt) của chúng tôi được biên soạn bám sát sách Toán 8 Tập 1 & Tập 2 chương trình mới.

Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.