Hình thang lớp 5 (có lời giải)
Bài viết Chuyên đề Hình thang lớp 5 đầy đủ lý thuyết và các dạng bài tập đa dạng có lời giải từ cơ bản đến nâng cao giúp Giáo viên & Phụ huynh có thêm tài liệu dạy môn Toán lớp 5.
Hình thang lớp 5 (có lời giải)
Chỉ từ 150k mua trọn bộ Chuyên đề Toán lớp 5 nâng cao (Lý thuyết + Bài tập có lời giải) bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
1. Hình Thang:
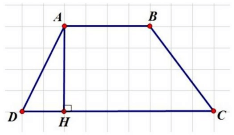
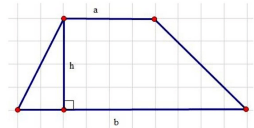
- Hình thang là tứ giác có hai cạnh đáy song song với nhau. (AB; CD)
- Hai cạnh còn lại là hai cạnh bên ( AD; BC)
- Đoạn thẳng giữa hai đáy và vuông góc với hai đáy gọi là đường cao hình thang (AH)
- Hình thang có 4 đỉnh: A; B; C: D.
- Hình thang có 4 góc: góc A; góc B; góc C; góc D.
- Trong hình thang ABCD có thể kẻ được nhiều đường cao và các đường cao đều bằng nhau.
2. Các dạng hình thang:
- Hình thang thường.
- Hình thang vuông:
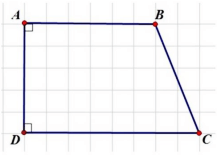
Có hai cạnh đáy vuông góc với một cạnh bên. Trong hình thang vuông thì cạnh bên vuông góc với hai đáy cũng là đường cao.
- Hình thang cân:
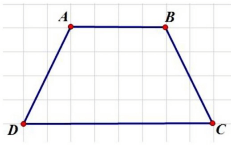
Là hình thang có hai cạnh bên bằng nhau (AD = BC)
3. Chu vi hình thang:
- Chu vi hình thang bằng tổng độ dài hai đáy và hai cạnh bên
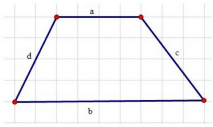
P = a + b + c + d.
4. Diện tích hình thang:
- Diện tích hình thang bằng tích của tổng độ dài hai đáy và chiều cao chia cho 2.
- Công thức:
- Các công thức phụ:
5. Một số ví dụ:
Ví Dụ 1: Một hình thang có chiều cao 56cm. Đáy bé kém đáy lớn 24cm và đáy bé bằng đáy lớn. Tính diện tích hình thang đó.
Giải
Đáy lớn của hình thang là: 24 : (5 – 2) × 5 = 40 (cm)
Đáy bé của hình thang là: 40 – 24 = 16 (cm)
Diện tích hình thang là: (cm²)
Đáp Số: 1568 cm².
Ví Dụ 2: Hình thang ABCD có đáy AB = 9cm và đáy CD = 12cm. Nếu kéo dài đáy bé thêm đoạn BE = 4cm và kéo dài đáy lớn thêm đoạn CG = 5cm thì diện tích hình thang ABCD sẽ tăng thêm 13,5cm². Tính diện tích hình thang ABCD.
Giải
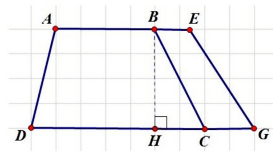
Phần diện tích tăng thêm là diện tích của hình thang BEGC.
Hình thang BEGC có chiều cao BH bằng chiều cao của hình thang ABCD.
Chiều cao của hình thang ABCD là: (cm)
Diện tích của hình thang ABCD là: (cm²)
Đáp Số: 31,5 cm².
Ví Dụ 3: Cho hình thang ABCD có đáy AB và CD. Hai đường chéo AC và BD cắt nhau tại điểm E. Biết rằng . Tìm tỉ số:
a)
b)
c)
Giải
a) Ta có: Chiều cao hạ từ A của tam giác ACD bằng chiều cao hạ từ C của tam giác CAB (cùng bằng chiều cao hình thang ABCD) mà nên (mà hai tam giác này chung đáy AC)
Lại có tam giác DAE và tam giác BAE chung đáy AE => (1)
Xét tam giác DAB và tam giác CAB: có chung đáy AB và có chiều cao bằng nhau (chiều cao hình thang)
(2)
Từ (1) và (2) có: mà hai tam giác BAE và CBE có chung chiều cao BG
Nên
b) Từ a) có
c) Ta có tam giác DAE và tam giác DEC có chung chiều cao DF và tỉ số hai cạnh đáy là: (3)
Từ (1) và (3) có:
Đáp Số: a) b) c)
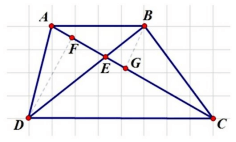
Ví Dụ 4: Cho hình thang ABCD có hai đáy là AB = 3cm và CD = 6cm. Hai đường chéo AC và BD cắt nhau tại điểm E. Biết diện tích hình tam giác ABE là 7cm². Tính diện tích hình thang ABCD.
Giải
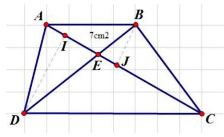
Có:
Tương tự như ví dụ 3 ta có:
Đáp Số: 63 cm².
Ví Dụ 5: Cho hình thang ABCD có hai đáy AB và CD. Biết CD = 3 x AB. Kéo dài hai cạnh bên DA và CB cắt nhau tại G. Tính diện tích hình thang ABCD, biết rằng diện tích hình tam giác GAB là 6 cm².
Giải
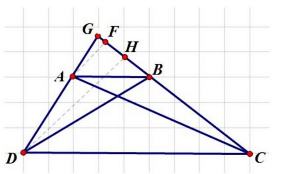
Hai tam giác DBC và ABC có chiều cao hạ từ B xuống CD bằng chiều cao hạ từ C xuông AB (bằng chiều cao hình thang ABCD) mà CD = 3 × AB
Suy ra: , lại có hai tam giác này chung đáy BC
Suy ra: DH = 3 × AF. Mà hai tam giác DGB và tam giác AGB chung đáy GB
Nên
Xét tam giác BCD và tam giác DAB:
- Có chiều cao hạ từ B xuống CD bằng chiều cao hạ từ D xuống AB (bằng chiều cao của hình thang ABCD)
- CD = 3 × AB.
Vậy:
Mà:
Đáp Số: 48 cm².
Bài tập tự luyện
Bài 1: Cho hình chữ nhật ABCD. Trên cạnh AB lấy điểm M và N sao cho AM = MN = NB.
a) Tính: b) Tính:
Bài 2: Cho hình thang ABCD có hai đáy là AB và CD. Hai đường chéo AC và BD cắt nhau tại điểm E. Hãy nêu tên các cặp hình tam giác có diện tích bằng nhau.
Bài 3: Cho hình thang ABCD có hai đáy là AB và CD. Trên AB lấy điểm M bất kỳ. Nối M với D và C. Trên DC lấy điểm N bất kỳ. Nối A với N cắt MD tại E. Nối B với N cắt MC ở G. Biết diện tích các hình tam giác AED và BGC lần lượt là 1,2cm² và 3,4cm². Tính diện tích hình tứ giác MBNE.
Bài 4: Cho hình thang ABCD có diện tích 108cm². Trên cạnh bên AD lấy hai điểm M và N sao cho AM = MN = ND. Trên cạnh bên BC lấy hai điểm E và G sao cho BE = EG = GC. Nối M với E và nối N với G được hình tứ giác MEGN. Tính diện tích hình tứ giác MEGN.
Bài 5: Cho hình tam giác ABC. Trên cạnh AB lấy hai điểm D và E sao cho AD = DE = EB. Trên cạnh AD lấy điểm M và N sao cho AM = MN = NC. Nối D với M và nối E với N được tứ giác DMNE có diện tích là 12 cm². Tính diện tích tam giác ABC.
Bài 6: Cho hình tam giác ABC có diện tích 32 cm². Trên cạnh AB lấy trung điểm M và trên MB lấy trung điểm N. Trên cạnh AC lấy trung điểm P và trên PC lấy trung điểm Q. Nối M với P và nối N với Q được tứ giác MPQN. Tính diện tích tứ giác MPQN.
Bài 7: Cho hình chữ nhật ABCD có AB = 4,5cm; BC = 3cm. Chia hình đó thành hình vuông AEGD và hình chữ nhật EBCG. Nối D với E. Đường chéo AC cắt DE ở M và cắt EG ở N. Tính diện tích hình tam giác NDC.
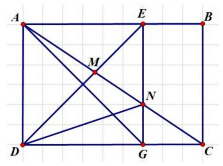
Bài 8: Cho hình thang ABCD có đáy bé AB và đáy lớn DC. Trên cạnh BC lấy trung điểm M. Nối M với A và nối M với D được hình tam giác AMD có diện tích 12,5 cm². Tính diện tích hình thang ABCD.
Bài 9: Cho hình thang ABCD có đáy bé AB và đáy lớn CD. Hai đường chéo AC và BD cắt nhau tại E. Biết diện tích các hình tam giác ABE và ADE lần lượt là 5 cm² và 15 cm². Tính diện tích hình thang ABCD.
Bài 10: Cho hình vuông ABCD cạnh 5cm. Từ B và D kẻ hai đường thẳng song song với AC. Từ A kẻ một đường thẳng cắt hai đường thẳng song song trên lần lượt tại E và F. Tính diện tích tam giác CEF.
Bài 11: Cho hình thang ABCD (đáy AD, BC) hai đường chéo AC, BD cắt nhau tại điểm M. Tính diện tích các tam giác MAB, MBC, MCD biết rằng AD = 20cm; BC = 10cm và đường cao của hình thang bằng 12cm.
................................
................................
................................
Xem thêm các chuyên đề Toán lớp 5 cơ bản và nâng cao hay, chọn lọc khác:
Tủ sách VIETJACK shopee lớp 1-5 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Tài liệu ôn tập và bồi dưỡng môn Tiếng Việt khối Tiểu học đầy đủ kiến thức trọng tâm môn Tiếng Việt lớp 3, 4, 5 và bài tập có hướng dẫn chi tiết.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

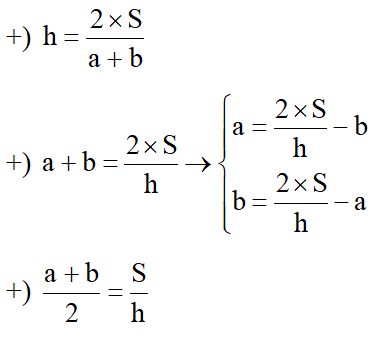
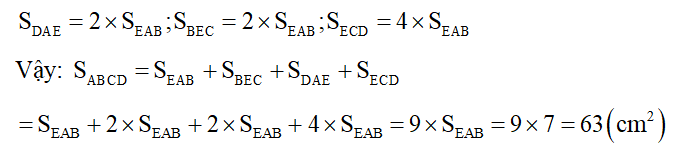



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

