15 Bài tập Hình thang cân lớp 8 (có đáp án)
Bài viết 15 Bài tập Hình thang cân có đáp án gồm các dạng bài tập về Hình thang cân lớp 8 từ cơ bản đến nâng cao giúp học sinh lớp 8 biết cách làm bài tập Hình thang cân.
15 Bài tập Hình thang cân lớp 8 (có đáp án)
(199k) Xem Khóa học Toán 8 KNTTXem Khóa học Toán 8 CTSTXem Khóa học Toán 8 CD
Bài 1: Điền cụm từ thích hợp vào chỗ trống
A. Hình thang cân là…………………………………..
B. Hình thang có………………. là hình thang cân .
C. Hai cạnh bên của hình thang cân…………………..
D. Hình thang cân có hai góc kề một đáy…………….
Lời giải:
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
→ Đáp án A điền: “hình thang có hai góc kề một đáy bằng nhau”.
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
→ Đáp án B điền: “hai góc kề một đáy bằng nhau”
+ Hai cạnh bên của hình thang cân bằng nhau.
→ Đáp án C điền: “bằng nhau”
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau
→ Đáp án D điền: “bằng nhau”
Bài 2: Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:
A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
B. Hình thang cân có hai cạnh bên bằng nhau.
C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.
D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
Lời giải:
+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
→ Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.
+ Hình thang cân có hai cạnh bên bằng nhau.
→ Đáp án B đúng.
+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
→ Đáp án D đúng, đáp án C sai.
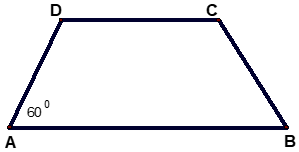
Bài 3: Cho hình thang cân ABCD (như hình vẽ) có BADˆ = 600. Số đo của BCDˆ = ?
A. 500 B. 600
C. 1200 D. 800
Lời giải:
Áp dụng tính chất của hình thang cân ta có:
Mà Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇔ 2Aˆ + 2Cˆ = 3600
⇒ 2Cˆ = 3600 - 2Aˆ = 3600 - 2.600 = 2400 ⇔ Cˆ = 1200
Chọn đáp án C.
Bài 4: Cho hình thang cân ABCD (AB // CD) . Tìm mệnh đề sai?
Lời giải:
Chọn đáp án D
Bài 5: Cho hình thang cân ABCD (AB// CD) và Dˆ = 80o. Tính ABCˆ
A. 100o B. 90o
C. 80o D. 110o
Lời giải:
Chọn đáp án A
Bài 6: Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?
A. ABCD là hình thang cân
B. AC = BD
C. BC = AD
D. Tam giác AOD cân tại O.
Lời giải:
* Ta có: OA = OB nên tam giác OAB cân tại O
* Do OC = OD nên tam giác OCD cân tại O
* vì OA = OB và OC = OD nên OA + OC = OB + OD
Hay AC = BD
Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.
Suy ra: BC = AD và BADˆ = ABCˆ; ADCˆ = DCBˆ
Chọn đáp án D
Bài 7: Cho hình thang cân ABCD có AB // CD và Aˆ = 125o. Tính Bˆ ?
A. 125o B. 65o
C. 90o D. 55o
Lời giải:
Theo định nghĩa hình thang cân ta có: Aˆ = Bˆ = 125o
Chọn đáp án A
Bài 8: Cho hình thang cân ABCD có AB// CD và AB = BC. Tìm khẳng định sai.
Lời giải:
* Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B.
Suy ra: BACˆ = ACBˆ
* Vì ABCD là hình thang cân nên AD = BC
Lại có AB = BC nên AB = AD.
* Suy ra: ΔABD cân tại A nên ADBˆ = ABDˆ
Chọn đáp án D
Bài 9: Cho hình thang cân ABCD có AB // CD. Gọi giao điểm của AD và BC là M . Tam giác MCD là tam giác gì ?
A. Tam giác cân B. Tam giác nhọn
C. Tam giác vuông D. Tam giác tù
Lời giải:
Vì ABCD là hình thang cân nên: Dˆ = Cˆ
Xét tam giác MCD có Dˆ = Cˆ nên đây là tam giác cân tại M
Chọn đáp án A
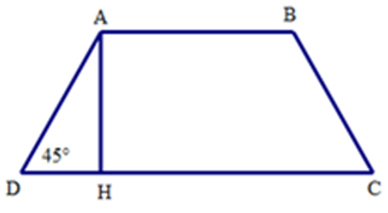
Bài 10: Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường AH = 5cm, và 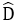
A. 13 cm
B. 10 cm
C. 12 cm
D. 8 cm
Lời giải
Ta có tam giác ADH vuông cân tại H vì 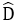
Do đó DH = AH = 5cm
Mà DH = 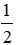
Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)
Vậy CD = 13 cm
Đáp án cần chọn là: A
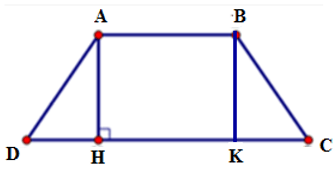
Bài 11: Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:
A. 4,5 cm
B. 4 cm
C. 3,5 cm
D. 3 cm
Lời giải
Kẻ BK ⊥ DC tại K.
Vì ABCD là hình thang cân nên ta có:
Do ABCD là hình thang cân nên AD = BC = 5 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
AD2 = AH2 + DH2
⇒ AH2 = AD2 – DH2 = 52 – 32
⇒ AH = 4
Vậy AH = 4cm
Đáp án cần chọn là: B
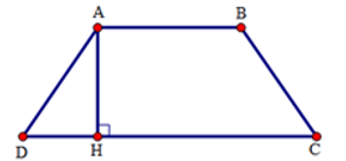
Bài 12: Cho hình thang cân ABCD đáy nhỏ AB = 12cm, đáy lớn CD = 22cm, cạnh bên BC = 13cm thì đường cao AH bằng:
A. 9 cm
B. 8 cm
C. 12 cm
D. 6 cm
Lời giải
Ta có:
Do ABCD là hình thang cân nên AD = BC = 13 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
AD2 = AH2 + DH2
⇒ AH2 = AD2 – DH2 = 132 – 52
⇒ AH = 12
Vậy AH = 12cm
Đáp án cần chọn là: C
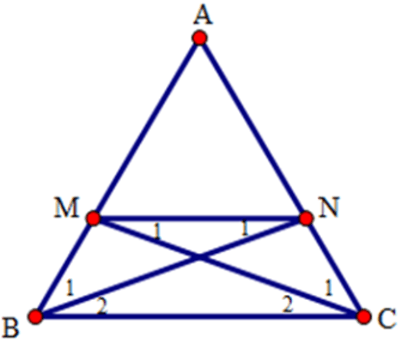
Bài 13: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
A. Hình thang
B. Hình thang cân
C. Hình thang vuông
D. Cả A, B, C đều sai
Lời giải
Ta có AB = AM + MB và AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)
Suy ra AN = AM
Xét tam giác AMN cân tại A.
Xét tam giác ANM có: 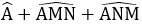
Xét tam giác ABC cân tại A ta có:
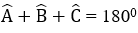
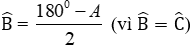
Từ (1) và (2) suy ra:
Mà 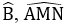
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có 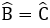
Đáp án cần chọn là: B
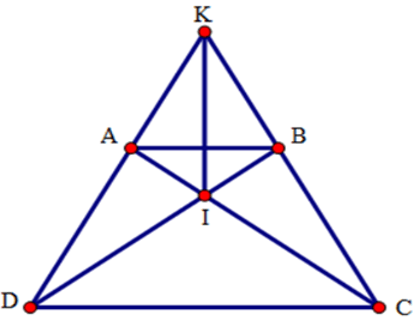
Bài 14: Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn khẳng định đúng:
A. KI là đường trung trực của hai đáy AB và CD
B. KI là đường trung trực của đáy AB nhưng không là đường trung trực của CD
C. KI là đường trung trực của đáy CD nhưng không là trung trực của AB
D. KI không là đường trung trực của cả hai đáy AB và CD.
Lời giải
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra 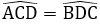
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.
Do đó KC = KD (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD (*).
Xét tam giác ADB và tam giác BCA có:
+ AD = BC (cmt)
+ AB là cạnh chung
+ AC = BD
Suy ra ΔADB = ΔBCA (c.c.c)
Suy ra 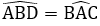
Xét tam giác IAB có 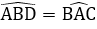
Do đó IA = IB (3)
Ta có KA = KD – AD; KB = KC – BC
Mà KD = KC, AD = BC, do đó KA = KB (4)
Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)
Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)
Đáp án cần chọn là: A
Bài 15: Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn câu sai.
A. ΔKAB cân tại K
B. ΔKCD cân tại K
C. ΔICD đều
D. KI là đường phân giác
Lời giải
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra 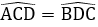
Nên C sai vì ta chưa đủ điều kiện để IC = CD
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.
Xét tam giác KDI và tam giác KCI có:
+ KD = KC (do ΔKCD cân tại K))
+ KI là cạnh chung
+ IC = ID
Suy ra ΔKDI = ΔKCI (c.c.c)
Suy ra 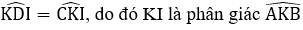
Ta có AB // CD (do ABCD là hình thang) nên 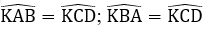
Mà 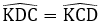
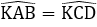
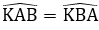
Đáp án cần chọn là: C
(199k) Xem Khóa học Toán 8 KNTTXem Khóa học Toán 8 CTSTXem Khóa học Toán 8 CD
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:
- Lý thuyết Hình thang cân
- Lý thuyết Đường trung bình của tam giác, của hình thang
- Bài tập Đường trung bình của tam giác, của hình thang
- Lý thuyết Dựng hình bằng thước và compa. Dựng hình thang
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Lý thuyết & 700 Bài tập Toán lớp 8 có lời giải chi tiết có đầy đủ Lý thuyết và các dạng bài có lời giải chi tiết được biên soạn bám sát nội dung chương trình sgk Đại số 8 và Hình học 8.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 8 Global Success
- Giải sgk Tiếng Anh 8 Smart World
- Giải sgk Tiếng Anh 8 Friends plus
- Lớp 8 - Kết nối tri thức
- Soạn văn 8 (hay nhất) - KNTT
- Soạn văn 8 (ngắn nhất) KNTT
- Giải sgk Toán 8 - KNTT
- Giải sgk Khoa học tự nhiên 8 - KNTT
- Giải sgk Lịch Sử 8 - KNTT
- Giải sgk Địa Lí 8 - KNTT
- Giải sgk Giáo dục công dân 8 - KNTT
- Giải sgk Tin học 8 - KNTT
- Giải sgk Công nghệ 8 - KNTT
- Giải sgk Hoạt động trải nghiệm 8 - KNTT
- Giải sgk Âm nhạc 8 - KNTT
- Lớp 8 - Chân trời sáng tạo
- Soạn văn 8 (hay nhất) - CTST
- Soạn văn 8 (ngắn nhất) - CTST
- Giải sgk Toán 8 - CTST
- Giải sgk Khoa học tự nhiên 8 - CTST
- Giải sgk Lịch Sử 8 - CTST
- Giải sgk Địa Lí 8 - CTST
- Giải sgk Giáo dục công dân 8 - CTST
- Giải sgk Tin học 8 - CTST
- Giải sgk Công nghệ 8 - CTST
- Giải sgk Hoạt động trải nghiệm 8 - CTST
- Giải sgk Âm nhạc 8 - CTST
- Lớp 8 - Cánh diều
- Soạn văn 8 Cánh diều (hay nhất)
- Soạn văn 8 Cánh diều (ngắn nhất)
- Giải sgk Toán 8 - Cánh diều
- Giải sgk Khoa học tự nhiên 8 - Cánh diều
- Giải sgk Lịch Sử 8 - Cánh diều
- Giải sgk Địa Lí 8 - Cánh diều
- Giải sgk Giáo dục công dân 8 - Cánh diều
- Giải sgk Tin học 8 - Cánh diều
- Giải sgk Công nghệ 8 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 8 - Cánh diều
- Giải sgk Âm nhạc 8 - Cánh diều

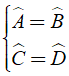
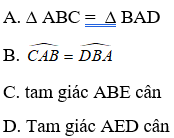

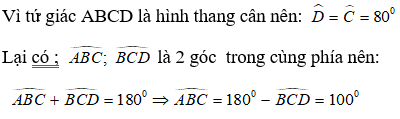
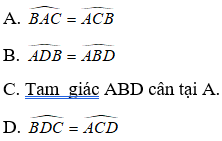
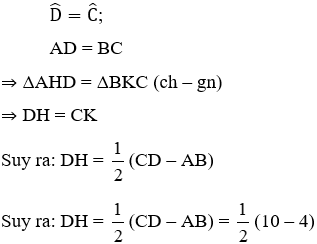
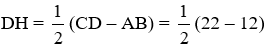
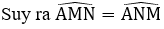
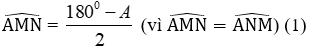
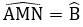
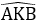



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

