Số bội giác là gì? Công thức tính số bội giác (chi tiết nhất)

Bài viết Số bội giác là gì? Công thức tính số bội giác với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Số bội giác là gì? Công thức tính số bội giác.

Số bội giác là gì? Công thức tính số bội giác (chi tiết nhất)

1. Số bội giác là gì?

Mỗi kính lúp có một số bội giác, kí hiệu là G, được ghi bằng các con số như 2X, 3X, 5X,... ngay trên vành đỡ kính.

Vậy kính lúp là gì?

Kính lúp hay kiếng lúp, tiếng Pháp: loupe là một thấu kính hộ i tụthường được dùng để khuếch đại hình ảnh, nó có đường kính từ vài cm đến vài chục cm, thường được bảo vệ bởi một khung, có thể thêm tay cầm. Nó là dạng đơn giản nhất của kính hiển vi. Kính lúp cho phép chúng ta vượt qua ranh giới nhìn gần để có thể quan sát một vật thể phóng đại lên nhiều lần (với mắt hường, khi vượt qua ranh giới này chúng ta không nhìn rõ được nữa).

Cách hoạt động của kính lúp là nhờ tạo ra một ảo ảnh nằm đằng sau kính, cùng phía với vật thẻ cần phóng đại, để thực hiện được điều này, kính phải đặt đủ gần vật thể, để khoảng cách giữa vật và kính nhỏ hơn tiêu cụ của kính.

Chúng ta có thể dùng kính lúp cho việc đọc chữ hay quan sát các vật thể nhỏ. Và dùng trong một số thí nghiệm khoa học đơn giản ở các trường học. Bên cạnh đó, kính lúp cũng là biểu hiển cho các chuyên gia trinh thám, họ dùng kính lúp để phóng to các dấu vết phạm tội. 

Độ phóng đại của kính lúp là thương số của tầm nhìn gần truyền thống là 25cm chia cho khoảng cách làm việc của kính lúp hay còn gọi là tiêu cự của kính. Kinh càng được đưa lại gần vật quan sát thì độ phóng càng to. Phóng đại bằng cách kéo lại gần vật, kính lúp thường có ghi số phóng đại như 27x, 20x, 15x,...đây chính là số tương ứng với tổng số lần phóng đại. Sau đó là con số ghi đường kính của kính với đơn bị là mm.

Số bội giác của kính lúp là gì?

Số bội giác hay độ bội giác (được viết tắt là G) của kính lúp cho biết, ảnh mà mắt thu được khi dùng kính lớn gấp bao nhiêu lần so với ảnh mà mắt thu được khi quan sát trực tiếp vật mà không dùng kính. Ví dụ, nếu kính lúp có số bội giác là 2x, điều này có nghĩa là khi nhìn qua kính lúp bạn nhìn thấy ảnh lớn gấp đôi so với ảnh ban đầu. Tương tự, nếu kính lúp có số bội giác là 3x, bạn nhìn thấy ảnh lớn gấp ba lần so với ảnh ban đầu. Như vậy số bội giác của kính lúp chỉ ra mức độ khuếch đại của kính, cho phép chúng ra nhìn thấy chi tiết nhỏ hơn một cách rõ hơn.

Số bội giác là một trong những chỉ số vô cùng quan trọng để xác định độ phóng đại. Trong ngành khoa học kính quang học, độ bội giác sẽ cho người sử dụng biết được mức độ phóng đại mà kính quang học mang lại.

Số bội giác là đại lượng đặc trung cho các dụng cụ quang học bổ trợ cho mắt, được xác định bằng thương số giữa góc trông ảnh qua dụng cụ quang học và góc trông trực tiếp vật.

Số bội giác cũng là một thông số quan trọng để người ta đánh giá về chất lượng của kính và xác định độ phóng đại, số bội giác càng lớn thì độ phóng đại của nó càng to và chất lượng của kính càng cao và ngược lại số bội giác càng nhỏ thì độ phóng đại càng thấp và chất lượng của kính không được tốt.

Điều này rất hữu ích và có ý nghĩa lớn trong nhiều lĩnh vực y học, sửa chữa các đồ điện tử, xem các vật nhỏ hay thậm chí việc đọc sách. Trong lĩnh vực giáo dục, số bội giác cho biết ảnh mà mắt thu được khi dùng kính lớn gấp bao nhiêu lần so với ảnh ban đầu. Điều này có thể giúp cho việc nghiên cứu và quan sát các đổi tượng nhỏ như vi khuẩn, tế bào hay các loài sinh vật nhỏ trong tự nhiên trở nên dễ dàng hơn. Hay dùng để đọc các nhãn hiệu trên các sản phẩm nhỏ như hộp thuốc, chai thuốc hay nhãn mác trên quần áo có chữ nhỏ. Trong mỹ thuật và điêu khắc, số bội giác của kính lúp giúp cho nghệ sĩ, nghệ nhân có thể tăng cường khả năng nhìn rõ các chi tiết nhỏ trong mỹ thuật và khắc, tạo ra các tác phẩm tinh xảo hơn.

2. Cách tính độ bội giác

Công thức số bội giác hay độ bội giác là một khái niệm quan trọng trong toán học và khoa học tự nhiên. Nó có vai trò quan trọng trong việc hiểu sự gia tăng hoặc giảm thiểu của một đại lượng dựa trên một tỉ lệ cụ thể. 

Cách 1: Khi ngắn chừng ở vô cực (điểm cực viễn)

Khoảng cách từ quang tâm của thấu kính mắt đến điểm cực cận của mắt (đối với mắt không có tật trong vật lý) người ta thường lấy bằng 25cm. Vậy, giữa số bội giác và tiêu cự f (đo bằng cm) của một kính lúp có hệ thức như sau:

$G=\frac{25}{f}$

Trong đó:

- G: số bội giác

- f: tiệu cự của kính được tính bằng cm. (Tiêu cự là khoảng cách tính từ tâm kính cho đến vật và kính chỉ có thể sử dụng trong khảng tiêu cự đó mà thôi)

Cách 2: Khi ngắm ở từng vị trí

 Công thức đơn giản để tính số bội giác là:

$G=\frac{\tan \alpha }{\tan {\alpha }_0}$

Trong đó:

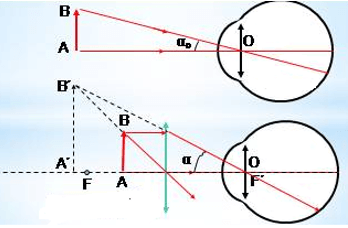
- α: Góc trông qua ảnh kính lúp

- α₀: Góc trông vật có giá trị lớn nhất

Trong trường hợp góc trông nhỏ, ta có thể xấp xỉ tan α bằng α và tan α₀ bằng α₀.

3. Định nghĩa

- Kính lúp là dụng cụ quang bỗ trợ cho mắt để quan sát các vật nhỏ, được cấu tạo bởi một thấu kính hội tụ (hoặc hệ ghép tương đương với thấu kính hội tụ) có tiêu cự nhỏ (cỡ cm). Kính lúp có tác dụng tạo ảnh với góc trông lớn hơn góc trông vật nhiều lần. 

- Cách sử dụng kính lúp

+ Đặt vật trong khoảng từ quang tâm O đến tiêu điểm vật chính F của kính lúp để có ảnh ảo cùng chiều và lớn hơn vật. 

+ Ngắm chừng: điều chỉnh khoảng cách từ vật đến thấu kính để ảnh  hiện ra trong giới hạn nhìn rõ của mắt. 

+ Khi cần quan sát trong một thời gian dài, ta nên thực hiện cách ngắm chừng ở cực viễn để mắt không bị mỏi.

Số bội giáclà đại lượng đặc trưng cho các dụng cụ quang học bổ trợ cho mắt, được xác định bằng thương số giữa góc trông ảnh qua dụng cụ quang học và góc trông trực tiếp vật:

4. Công thức – đơn vị đo

Số bội giác được định nghĩa là: $G=\frac{\alpha }{{\alpha }_0}$

Vì các góc α và α₀ đều rất nhỏ, nên ta có thể xác định

$G=\frac{\alpha }{{\alpha }_0}\approx \frac{\tan \alpha }{\tan {\alpha }_0}$

Mà góc trông vật α₀ có giá trị lớn nhất khi vật đặt ở điểm cực cận (C_C) nên 

$\tan {\alpha }_0=\frac{AB}{O{C}_C}; \tan \alpha =\frac{A^{\text{'}}{B}^{\text{'}}}{O{A}^{\text{'}}}$

- Công thức tổng quát cho các trường hợp: $G=\left|k\right|.\frac{O{C}_C}{\left|O{A}^{\text{'}}\right|+L}$

* Khi ngắm chừng ở cực cận: OA^' = OC_C nên $G_C=\frac{A^{\text{'}}{B}^{\text{'}}}{AB}$= |k|

* Khi ngắm chừng ở cực viễn: OA^' = OC_V nên $G=\left|k\right|.\frac{O{C}_C}{O{C}_V}$

Trong đó:

+ α₀ là góc trông khi nhìn trực tiếp bằng mắt khi vật đặt tại điểm cực cận;

+ α là góc trông ảnh khi nhìn qua kính lúp.

+ G là số bội giác

+ k là số phóng đại ảnh

+ L là khoảng cách từ kính lúp tới mắt

5. Mở rộng      

Đối với người có mắt tốt, cực viễn ở vô cùng, vì vậy, số bội giác khi ngắm chứng ở vô cực được tính bằng công thức:

$G=\frac{O{C}_C}{f}$ (với f là tiêu cự kính lúp)

6. Bài tập vận dụng

Câu 1: Một kính lúp có số bội giác 5x, tiêu cự của kính lúp có giá trị là:

A. 5 cm

B. 5 m

C.5 mm

D. 5 dm

Giải chi tiết:

Số ghi trên vành kính lúp là số bội giác của kính.

Công thức tính số bội giác: với f là tiêu cự của kính, Kính này có ghi 5x có nghĩa số bội giác bằng nên ta có tiêu cự của kính lúp bằng 5cm.

Chọn A.

Câu 2: Một người mắt bình thường có khoảng cách nhìn rõ ngắn nhất là 20cm quan sát một vật nhỏ nhờ một kính lúp trên vành ghi 5x. Kính lúp đặt sát mắt

 a, Hỏi vật phải đặt trong khoảng nào trước kính lúp

 b, Tính số bội giác của kính khi ngắm chừng ở điểm cực cận và ở vô cực

Đáp án:

a, $4cm\le d\le 5cm$

b, Khi ngắm chừng ở điểm cực cân: 5

Khi ngắm chừng ở vô cực: 4

Câu 3: Một người cận thị có khoảng cách nhìn rõ nhất là 15cm và giới hạn nhìn rõ là 35cm. Người này quan sát một vật nhỏ qua kính lúp có tiêu cự 5cm. Mắt đặt cách kính 10cm.

a, Phải đặt vật trong khoảng nào trước kính

b, Tính số bội giác của kính trong trường hợp người này ngắm chừng ở điểm cực viễn và điểm cực cận

Đáp án:

a, Phải đặt vật trước kính đoạn từ 2,5 cm đến 40/9 cm

b, Độ bội giác khi ngắm chừng ở cực cận: 2

Độ bội giác khi ngắm chừng ở điểm cực viễn: 2,7

Câu 4: Một người cận thị có khoảng cách từ mắt đến điểm cực cận là 10 cm và đến điểm cực viễn là 50 cm, quan sát một vật nhỏ nhờ một kính lúp có tiêu cực f = 4 cm. Kính lúp đặt cách mắt 2 cm.

a, Phải đặt vật trong khoảng nào trước kính

b, Tính số bội giác của kính lúp khi đặt vật trước kính và cách kính 3,5 cm

c, Tính số bội giác của kính lúp khi ngắm chừng ở cực cận

d, Tính số bội giác của kính lúp khi ngắm chừng ở cực viễn.

Đáp án:

a, Vậy phải đặt vật trong khoảng từ 8/3 cm đến 48/13 cm trước kính lúp

b, Số bội giác của kính khi đặt vật trước kính và cách kính 3,5 cm: G = $\frac{8}{3}$

c, Khi ngắm chừng ở điểm cực cận: Số bội giác = 3 cm

d, Số bội giác khi ngắm chừng ở điểm cực viễn: 2,6

Câu 5: một người đứng tuổi khi nhìn những vật ở xa thì không phải đeo kính nhưng khi đeo kính sát mắt thì có độ tụ +1dp thì đọc được sách cách mắt gần nhất 25cm.

a, Xác định vị trí điểm cực cận và điểm cực viễn của mắt người này

b, Xác định độ biến thiên độ tụ của mắt người này từ trạng thái không điều tiết đến điều tiết tối đa

c, Người này bỏ kính ra và dùng một kính lúp có độ tụ 32dp để quan sát một vật nhỏ. Mắt cách kính 30 cm, phải đặt vật trong khoảng nào trước kính? Tính số bội giác khi ngắm chừng ở vô cực.

Hướng dẫn:

Vật cách kính từ 1,613 cm đến 3,125 cm và G = 10,67

Câu 6: Một người có điểm cực cận cách mắt 25 cm, sử dụng một kính lúp có tiêu cự f = 5 cm để quan sát một vật nhỏ. Kính đặt cách mắt 10 cm. Tính số bội giác của kính lúp khi ngắm chừng ở cực cận.

Bài giải:

Vì kính đặt cách mắt 10 cm nên ảnh hiện ra ở cực cận cách mắt 15 cm, ta có d’ = -15 cm.

Áp dụng công thức thấu kính:

$\frac{1}{f}=\frac{1}{d}+\frac{1}{d^{\text{'}}}\Rightarrow d=\frac{d^{\text{'}}.f}{d^{\text{'}}-f}=\frac{-15.5}{-15-5}=\frac{15}{4}=3,75\left(cm\right)$

Khi ngắm chừng ở cực cận: OA^' = OC_C nên $G_C=\frac{A^{\text{'}}{B}^{\text{'}}}{AB}$= |k_C| = $|-\frac{d^{\text{'}}}{d}|=|-\frac{-15}{3,75}|=4$

Câu 7: Một người mắt tốt có thể nhìn xa vô cùng mà không cần điều tiết, sử dụng một kính lúp có tiêu cự f = 2,5 cm để quan sát một vật nhỏ. Biết khoảng cực cận của mắt người này là 25 cm. Tính số bội giác khi ngắm chừng ở vô cực.

Bài giải:

Áp dụng công thức $G=\frac{O{C}_C}{f}=\frac{25}{2,5}=10$

Xem thêm các dạng bài tập Vật Lí sách mới hay, chi tiết khác:

• Quỹ đạo chuyển động là gì? Công thức tính quỹ đạo chuyển động

• Tia tử ngoại là gì? Công thức tính tia tử ngoại

• Nam châm là gì? Công thức tính nam châm

• Vật sáng là gì? Công thức tính vật sáng

• Áp suất là gì? Công thức tính áp suất

• Sai số là gì? Công thức tính sai số

---