Sách bài tập Toán 9 Bài 2: Đường kính và dây của đường tròn

Sách bài tập Toán 9 Bài 2: Đường kính và dây của đường tròn

Bài 15 trang 158 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC, các đường cao BH và CK. Chứng minh:

a. Bốn điểm B, C, H, K cùng thuộc một đường tròn

b. HK < BC

Lời giải:

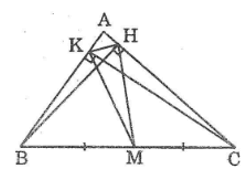
a. Gọi M là trung điểm của BC.

Tam giác BCH vuông tại H có HM là đường trung tuyến nên:

HM = (1/2).BC (tính chất tam giác vuông)

Tam giác BCK vuông tại K có KM là đường trung tuyến nên:

KM = (1/2).BC (tính chất tam giác vuông)

Suy ra: MB = MC = MH = MK

Vậy bốn điểm B, C, H, K cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).BC.

b. Trong đường tròn tâm M ta có KH là dây cung không đi qua tâm, BC là đường kính nên: KH < BC

Bài 16 trang 159 Sách bài tập Toán 9 Tập 1: Tứ giác ABCD có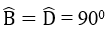

a. Chứng minh rằng bốn điêm A, B, C, D cùng thuộc một đường tròn

b. So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì?

Lời giải:

a. Gọi M là trung điểm của AC

Tam giác ABC vuông tại B có BM là đường trung tuyến nên:

BM = (1/2).AC (tính chất tam giác vuông)

Tam giác ACD vuông tại D có DM là đường trung tuyến nên:

DM = (1/2).AC (tính chất tam giác vuông)

Suy ra: MA = MB = MC = MD

Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).AC.

b. Trong đường tròn tâm M ta có BD là dây cung không đi qua tâm, AC là đường kính nên: BD < AC

AC = BD khi và chỉ khi BD là đường kính. Khi đó tứ giác ABCD là hình chữ nhật.

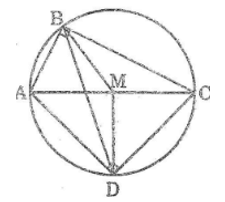
Bài 17 trang 159 Sách bài tập Toán 9 Tập 1: Cho nửa đường tròn tâm O, đường kính AB và dây EF không cắt đường kính. Gọi I và K lần lượt là chân các đường vuông góc kẻ từ A và B đên EF. Chứng minh rằng IE = KF.

Lời giải:

Ta có: AI ⊥ EF (gt)

BK ⊥ EF (gt)

Suy ra: AI // BK

Suy ra tứ giác ABKI là hình thang

Kẻ OH ⊥ EF

Suy ra: OH // AI // BK

Ta có: OA = OB (= R)

Suy ra: HI = HK

Hay: HE + EI = HF + FK     (1)

Lại có: HE = HF (đường kính dây cung)    (2)

Từ (1) và (2) suy ra: IE = KF

Bài 18 trang 159 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.

Lời giải:

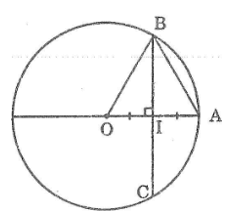
Gọi I là trung điểm của AB

Suy ra: IO = IA = (1/2).OA = 3/2

Ta có: BC ⊥ OA (gt)

Suy ra: góc (OIB) = 90^o

Áp dụng định lí Pitago vào tam giác vuông OBI ta có: OB² = BI² + IO²

Suy ra: BI² = OB² - IO²

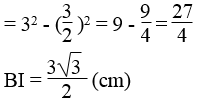
Ta có: BI = CI (đường kính dây cung)

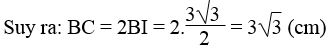
Bài 19 trang 159 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C.

a. Tứ giác OBDC là hình gì? Vì sao?

b. Tính số đo các góc CBD, CBO, OBA

c. Chứng minh rằng tam giác ABC là tam giác đều.

Lời giải:

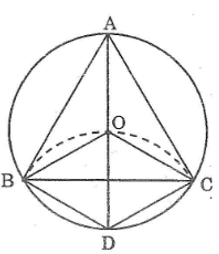
a. Ta có:

OB = OC = R (vì B, C nằm trên (O; R))

DB = DC = R (vì B, C nằm trên (D; R))

Suy ra: OB = OC = DB = DC

Vậy tứ giác OBDC là hình thoi

b. Ta có: OB = OC = BD = R

Bài 20 trang 159 Sách bài tập Toán 9 Tập 1: a. Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN

b. Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.

Lời giải:

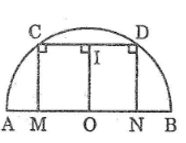
a. Ta có: CM ⊥ CD

DN ⊥ CD

Suy ra: CM // DN

Kẻ OI ⊥ CD

Suy ra: OI // CM // DN

Ta có: IC = ID (đường kính dây cung)

Suy ra: OM = ON    (1)

Mà: AM + OM = ON + BN (= R)    (2)

Từ (1) và (2) suy ra: AM = BN

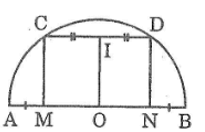
b. Ta có: MC // ND (gt)

Suy ra tứ giác MCDN là hình thang

Lại có: OM + AM = ON + BN (= R)

Mà AM = BN (gt)

Suy ra: OM = ON

Kẻ OI ⊥ CD     (3)

Suy ra: IC = ID (đường kính dây cung)

Khi đó OI là đường trung bình của hình thang ACDN

Suy ra: OI // MC // ND     (4)

Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.

Bài 21 trang 159 Sách bài tập Toán 9 Tập 1: Cho đường tròn tâm O, đường kính AB. Dây CD cắt đường kính AB tại I. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK

Lời giải:

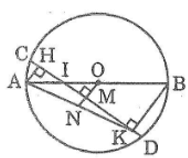
Kẻ OM ⊥ CD cắt AD tại N

Ta có: MC = MD (đường kính dây cung)

Hay MH + CH = MK + KD     (1)

Ta có: OM // BK (cùng vuông góc với CD)

Hay: MN // BK

Mà: OA = OB (= R)

Suy ra: NA = NK (tính chất đường trung bình của tam giác)

Lại có: OM // AH (cùng vuông góc với CD)

Hay: MN // AH

Mà: NA = NK (chứng minh trên)

Suy ra: MH = MK (tính chất đường trung bình của tam giác)    (2)

Từ (1) và (2) suy ra: CH = DK

Bài 22 trang 159 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O; R) và điểm M nằm bên trong đường tròn.

a. Hãy nêu cách dựng dây AB nhận M làm trung điểm

b. Tính độ dài AB ở câu a biết rằng R = 5cm, OM = 1,4cm

Lời giải:

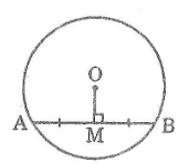
a. * Cách dựng

- Dựng đoạn OM

- Qua M dựng đường thẳng vuông góc với OM cắt O tại A và B.

Nối A và B ta được dây cần dựng

*Chứng minh

Ta có: OM ⊥ AB ⇒ MA = MB

b. Áp dụng định lí Pitago vào tam giác vuông OMB ta có:

OB² = OM² + MB²

Suy ra: MB² = OB² - OM² = 5² - 1,4² = 25 - 1,96 = 23,04

MB = 4,8 (cm)

Vậy AB = 2.MB = 2.4,8 = 9,6 (cm)

Bài 23 trang 159 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. Hãy cho biết ACBD là hình gì? Vì sao?

Lời giải:

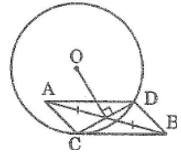
Ta có: OI ⊥ CD (gt)

Suy ra: IC = ID (đường kính dây cung)

Mà: IA = IB (gt)

Tứ giác ACBD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.

Bài 1 trang 159 Sách bài tập Toán 9 Tập 1: Độ dài cạnh của tam giác đều nội tiếp đường tròn (O;R) bằng

A. R/2;        B. (R√3)/2;

C. R√3;        D. Một đáp án khác.

Hãy chọn phương án đúng.

Lời giải:

Chọn đáp án C

Bài 2 trang 160 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 2cm). Vẽ hai dây AB và CD vuông góc với nhau. Tính diện tích lớn nhất của tứ giác ABCD.

Lời giải:

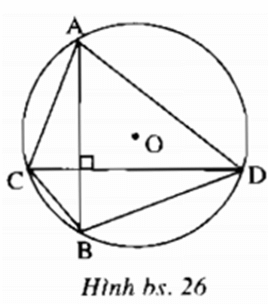
Ta có AB ≤ 4cm, CD ≤ 4cm. Do AB ⊥ CD nên S_ACBD = 1/2AB.CD ≤ 1/2.4.4 = 8 (cm²)

Giá trị lớn nhất của S_ACBD bằng 8 cm² khi AB và CD đều là đường kính của đường tròn.

Xem thêm Video Giải sách bài tập Toán lớp 9 (SBT Toán 9) hay và chi tiết khác:

• Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
• Bài 4: Vị trí tương đối của đường thẳng và đường tròn
• Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn.
• Bài 6: Tính chất của hai tiếp tuyến cắt nhau

Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:

• Giải bài tập Toán 9
• Chuyên đề Toán 9 (có đáp án - cực hay)
• Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
• Các dạng bài tập Toán 9 cực hay
• Đề thi Toán 9
• Đề thi vào 10 môn Toán

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---