Các bài toán về dấu hiệu chia hết (Ôn thi vào lớp 6)

Nhằm mục đích giúp học sinh nắm vững được cấu trúc và các dạng toán hay có trong đề thi vào lớp 6 môn Toán, VietJack biên soạn tài liệu Các bài toán về dấu hiệu chia hết có lời giải đầy đủ phương pháp giải, ví dụ minh họa và bài tập tự luyện giúp học sinh ôn luyện và đạt điểm cao trong kì thi tuyển sinh vào lớp 6 môn Toán.

Các bài toán về dấu hiệu chia hết (Ôn thi vào lớp 6)

I. Các dạng toán

Dạng 1. Dùng dấu hiệu chia hết để viết số tự nhiên

1. Phương php

Bước 1. Gọi số cần tìm có dạng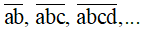

Bước 2. Sử dụng dấu hiệu chia hết 2, 3, 5, 9 để lựa chọn các giá trị thích hợp cho từng chữ số.

2. Ví dụ  1

Cho 5 chữ số: 0, 1, 2, 4, 5. Từ  5 chữ số đã cho có thể viết được:

1. Bao nhiêu số có 4 chữ số chia hết cho 5 ?

2. Có thể viết bao nhiêu chữ số có 4 chữ số khác nhau chia hết cho 5 mà chữ số hàng trăm bằng 4 ?

3. Có thể viết được bao nhiêu số lẻ có 5 chữ số khác nhau chia hết cho 5 ?

Bài giải

a) Số cần tìm có dạng  :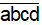

- Có 4 cách chọn a (1, 2, 3, 4)

- Có 5 cách chọn b (0, 1, 2, 4, 5)

- Có 5 cách chọn c (0, 1, 2, 4, 5)

- Có 2 cách chọn d (0, 5 )

Ta có : 4 5 5 2 = 200 cách chọn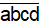

Kết luận: Có 200 số có 4 chữ số chia hết cho 5.

b) Số cần tìm có dạng 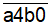hoặc .

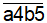+ Nhóm 1: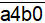

- Có 3 cách chọn a ( 1, 2, 5 )

- Có 2 cách chọn b ( 3 cách trừ 1 cách đã chọn a)

Ta có : 3 2 = 6 cách chọn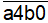

+ Nhóm 2: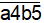

- Có 2 cách chọn a ( 1, 2 )

- Có 2 cách chọn b ( 0 và 1 hoặc 2 )

Ta có : 2 2 = 4  cách chọn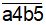

Kết luận: Có thể viết 10 số  ( 6+ 4 = 10 ) có 4 chữ số  chia hết cho 5 mà chữ số hàng trăm bằng 4.

c) Số phải tìm có dạng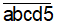  

- Có 3 cách chọn a ( 1, 2, 4 )

- Có 3 cách chọn b ( 0 và 2 chữ số còn lại)

- Có 2 cách chọn c ( 2 chữ số còn lại)

- Có 1 cách chọn d ( chữ số cuối cùng)

Ta có  3 3 2 1 = 18 cách chọn số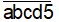

Kết luận: Có thể viết được 18 số lẻ có 5 chữ số khác nhau chia hết cho 5.

Dạng 2: Dùng dấu hiệu chia hết để tìm các chữ số chưa biết của một số tự nhiên

1. Phương pháp

Áp dụng dấu hiệu chia hết

2. Ví dụ 

Ví dụ 1. Thay a và b bởi các chữ số thích hợp để nhận được số tự nhiên A = 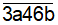 là số có 5 chữ số khác nhau chia hết cho 3 và 4.

Bài giải

- Vì A chia hết cho 4 nên 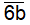( 2 chữ số tận cùng) chia hết cho 4. Suy ra b = 0, 4, 8.

- Vì A có 5 chữ số khác nhau nên  b = 0 và 8.

+ Khi b = 0 , A có dạng : .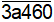  

Vì A chia hết cho 3 nên  3 + a + 4 + 6 + 0 = a + 13 chia hết cho 3. Suy ra  a = 2, 5, 8

Số phải tìm là: 32460, 35460, 38460.

+ Khi b = 8, A có dạng :

Vì A chia hết cho 3 nên  3 + a + 4 + 6 + 8 = a + 21 chia hết cho 3. Suy ra  a = 0, 3, 6, 9.

Vì A có 5 chữ số khác nhau nên ta chọn  a = 0 và 9

Số phải tìm là 30468, 39468

Kết luận: Các số cần tìm là32460, 35460, 38460, 30468, 39468.

Ví dụ 2. Cho số 47, hãy viết 1 chữ số bên phải và 1 chữ số bên trái để nhận được số lớn nhất có 4 chữ số chia hết cho 2, 3 và 5.

Bài giải

Gọi chữ viết thêm vào bên phải là a, số bên trái là b. Số phải tìm có dạng A=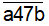

- Vì A chia hết cho 2 nên b= 0, 2, 4, 6, 8.

- Vì A chia hết cho 5 nên b= 0, 5. 

- Vì A chia hết cho 2 và 5 nên b= 0. Thay b= 0 vào A ta có :

Số phải tìm A là A =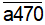

- Vì A chia hết cho 3 nên : 

a+ 4 + 7 + 0 = a + 11 chia hết cho 3

Suy ra a = 1, 4, 7.

Để A là số lớn nhất có 4 chữ số, ta  chọn a = 7.

Số phải tìm là : 7470.

Dạng 3: Các bài toán về phép chia có dư

1. Phương pháp

- Một số chia cho 2 dư 1 thì chữ số hàng đơn vị của nó bằng 1, 3, 5, 7, 9.

- Một số chia cho 5 dư 1 thì chữ số hàng đơn vị của nó bằng 1 hoặc 6; nếu dư 2 thì hàng đơn vị bằng 2 hoặc 7; nếu dư 3 thì hàng đơn vị bằng 3 hoặc 8; nếu dư 4 thì hàng đơn vị bằng 4 hoặc 9.

- Số tự nhiên A và tổng các chữ số của nó khi chia cho 9 có cùng số dư.

- Nếu A chia cho B dư 1 thì A – 1 sẽ chia hết cho B.

- Nếu A chia cho B dư B – 1 thì A + 1 sẽ chia hết cho B.

2. Ví dụ

Ví dụ 1. Thay a và b bởi các chữ số thích hợp để nhận được số tự nhiên n =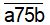 là số có 4 chữ số khác nhau khi chia cho 2, 5, 9 đều dư 1:

Bài giải

- Vì n chia cho 5 dư 1 nên b = 1, 6.

+ Nếu b = 1, thay vào n ta có : n=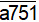

- Vì n chia cho 9 dư 1 nên a + 7 + 5 + 1 = a + 13 chia cho 9 dư 1. Suy ra a = 6.

- Vì n chia cho 3 dư 1 nên a + 7 + 5 + 1 = a + 13 chia cho 3 dư 1. Suy ra a = 3 hoặc 6 hoặc 9.

- Vì n chia cho 3 hoặc 9 đều dư 1 nên ta chọn a = 6. 

Thay a = 6 vào n, ta có n = 6751.

+ Nếu b = 6 thay vào n ta có : n =

- Vì n chia cho 9 dư 1 nên a + 5 + 7 + 6 = a + 18 chia cho 9 dư 1. Suy ra a = 1.

- Vì n chia cho 3 dư 1 nên a + 5 + 7 + 6 = a + 18 chia cho 3 dư 1. Suy ra a = 1 hoặc 4 hoặc 7.

- Vì n chia cho 3 hoặc 9 đều dư 1 nên ta chọn a = 1. 

Thay a = 1 vào n, ta có n = 1756.

Kết quả:

a = 6 và b = 1 ta có n = 6751.

a = 1 và b = 6 ta có n = 1756.

Ví dụ 2. Viết thêm vào bên phải số 91 ba chữ số để nhận được một số có năm chữ số khác nhau khi chia cho 2 dư 1 , chia cho 5 dư 3, chia cho 9 không dư.

Bài giải

Gọi số phải tìm là n =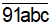 ta có:

- Vì n chia cho 5 dư 3 nên c = 3 hoặc 8 (1)

- Vì n chia cho 2 dư 1 nên c = 1, 3, 5, 7, 9 (2).

1. và (2) suy ra: c = 3.

Thay c = 3 vào n: n =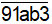

- Vì n chia hết cho 9 nên 9 + 1 + a + b + 3 = a + b + 13 chia hết cho 9. Suy ra a + b = 5 hoặc 14.

+ Nếu a + b = 5  thì:

a = 0; b = 5 hay a = 5 ; b = 0.

a = 1; b = 4 hay a = 4 ; b = 1.

a = 2; b = 3 hay a = 3 ; b = 2.

Do n là các chữ số khác nhau nên chọn a = 0, b = 5 hoặc a = 5, b = 0.

- Nếu a = 0 thay vào n: n = 91053.

- Nếu a = 5 thay vào n: n = 91503.

+ Nếu a + b = 14 thì:

a = 8 ; b = 6 hoặc a = 6, b = 8.

- Nếu a = 8 thay vào n: n = 91863.

- Nếu a = 6 thay vào n: n = 91683.

Ví dụ 3. Cho số tự nhiên A. Viết các chữ số của A theo thứ tự ngược lại ta được số tự nhiên B lớn gấp 3 lần A. Chứng tỏ rằng A chia hết cho 9.

Bài giải

Vì B = 3A nên tổng các chữ số của B chia hết cho 3, tổng các chử số của A cũng chia hết cho 3. 

Vì B và A có các chữ số bằng nhau nên tổng các chữ số của A và B bằng nhau và chia hết cho 3.

Vì A chia hết cho 3 nên A = 3k (k là số tự nhiên).

Suy ra B = 3A = 3x3k = 9 x k

Suy ra B chia hết cho 9.

Vì B chia hết cho 9 nên tổng các chữ số của B chia hết cho 9.

Suy ra tổng các chữ số của A cũng chia hết cho 9.

Suy ra A chia hết cho 9.

Ví dụ 4. Không làm phép tính hãy cho biết kết quả sau đúng hay sai: 723 +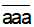 = 1235 ?

Bài giải

723 chia hết cho 3 vì 7 + 2 + 3 = 12 (chia hết cho 3).

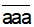 tổng các chữ số  3 a chia hết cho 3.

 Vì 1235 có 1 + 2 + 3 + 5 = 11 không chia hết cho 3 nên bài tính sai.

II. Bài tập vận dụng

Bài 1: Cho 6 chữ số: 0, 1, 4, 5, 7, 8:

a) Có thể viết được bao nhiêu số có 3 chữ số chia hết cho 5 từ 6 chữ số đã cho.

b) Có bao nhiêu số lẻ có 4 chữ số khác nhau chia hết cho 5 mà chính số hàng trăm bằng 1.

c) Có bao nhiêu số chẵn có 5 chữ số khác nhau chia hết cho 5 mà chính số hàng chục là số lẻ.

d. Có bao nhiêu số có 4 chữ số khác nhau chia hết cho 2 và 5 lớn hơn 2004.

Bài 2: Thay x và y bởi các chữ số thích hợp để nhận được số tự nhiên 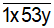 là số có 5 chữ số khác nhau chia hết cho 3 và 5.

Bài 3: Hãy viết thêm vào bên phải số 123 ba chữ số để nhận được số nhỏ nhất có 6 chữ số khác nhau chia hết cho 2, 5 và 9.

Bài 4: Hãy viết thêm vào bên phải số 312 một chữ số và bên trái hai chữ số để nhận được số nhỏ nhất có 6 chữ số chia hết cho 4, 5 và 9.

Bài 5: Thay a và b bởi các chữ số thích hợp để nhận được số tự nhiên n =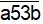 khi chia cho 3 dư 2, chia chọ dư 4. Tìm số nhỏ nhất và số lớn nhất thoả mản các điều kiện nói trên.

Bài 6: Hãy viết thêm vào bên trái số 714 hai chữ số và bên phải một chữ số để nhận được số nhỏ nhất có 6 chữ số khi chia cho 3, 4, 9 đều dư 1 và chia cho 5 thì không dư.

Bài 7: Cho số tự nhiên A. Viết các chữ số của A theo thứ tự ngược lại thì ta được số tự nhiên B gấp 9 lần A. Chứng minh rằng B chia hết cho 81.

Bài 8: Tìm số tự nhiên nhỏ nhất khác 1 sao cho khi chia cho 2; 3; 4; 5 và 7 đều dư 1.

Bài 9: Cho số a765b; tìm a; b để khi thay vào số đã cho ta được số có 5 chữ số chia cho 2 dư 1; chia cho 5 dư 3 và chia cho 9 dư 7.

Bài 10: Hãy viết thêm 3 chữ số vào bên phải số 567 để được số lẻ có 6 chữ số khác nhau, khi chia số đó cho 5 và 9 đều dư 1.

Bài 11: Tìm số có 4 chữ số chia hết cho 2; 3 và 5, biết rằng khi đổi chỗ các chữ số hàng đơn vị với hàng trăm hoặc hàng chục với hàng nghìn thì số đó không thay đổi.

Bài 12: Hãy viết tất cả các số có ba chữ số khác nhau từ bốn chữ số 0 ; 4 ; 5 ; 9 thỏa mãn điều kiện:

a) Chia hết cho 2

b) Chia hết cho 4

c) Chia hết cho 2 và 5

Bài 13

a) Có thể viết được bao nhiêu số chẵn có 3 chữ số mà các chữ số của nó đều là số chẵn.

b) Có thể viết được bao nhiêu số có bốn chữ số khác nhau chia hết cho 5 mà các chữ số của nó đều là số lẻ?

Bài 14.

a) Có thể viết được bao nhiêu số chẵn có 3 chữ số mà các chữ số của nó đều là số chẵn.

b) Có thể viết được bao nhiêu số có bốn chữ số khác nhau chia hết cho 5 mà các chữ số của nó đều là số lẻ?

Bài 15: Tìm a và b để $\overline{56a3b}$ chia hết cho 36.

Bài 16: Tìm a và b để số $\overline{a391b}$ chia hết cho 9 và chia cho 5 dư 1.

Bài 17: Cho số $\overline{5x1y5}$. Hãy tìm x và y để được số có 4 chữ số khác nhau chia hết cho 2, 3 và chia cho 5 dư 4.

Bài 18: Cho $A=\overline{x036y}$. Tìm x và y để A chia cho 2, 5 và 9 đều dư 1.

Bài 19: Hãy viết thêm ba chữ số vào bên phải số 567 để được một số lẻ có sáu chữ số khác nhau, khi chia số đó cho 5 và 9 đều dư 1.

Bài 20: Hãy viết thêm hai chữ số vào bên phải và một chữ số vào bên trái số 54 để được số lớn nhất có năm chữ số thỏa mãn tính chất: chia số đó cho 4 dư 3, cho 5 dư 4 và cho 9 dư 8.

Bài 21: Một cửa hàng hoa quả có 5 rổ đựng cam và chanh (trong mỗi rổ chỉ đựng một loại quả). Số quả trong mỗi rổ lần lượt là 104 ; 115 ; 132 ; 136 và 148 quả. Sau khi bán được 1 rổ cam, người bán hàng thấy rằng số chanh còn lại gấp 4 lần số cam. Hỏi lúc đầu cửa hàng có bao nhiêu quả mỗi loại?

Bài 22: Một cửa hàng thực phẩm có 7 rổ trứng gà và trứng vịt (mỗi rổ chỉ đựng một loại trứng). Số trứng trong mỗi rổ theo thứ tự lần lượt là: 45 ; 56 ; 60 ; 66 ; 75 ; 85 và 92 quả. Sau khi bán hết 6 rổ, chỉ còn lại 1 rổ trứng gà, người bán hàng thấy rằng trong số trứng đã bán, số trứng vịt gấp 3 lần số trứng gà. Hỏi lúc đầu cửa hàng có bao nhiêu quả trứng mỗi loại?

Bài 23: Một tháng có 3 chủ nhật là ngày chẵn. Hỏi ngày 15 của tháng đó là thứ mấy?

Bài 24: Một chuỗi các viên bi được sắp xếp theo quy luật sau: 5 viên xanh, 4 viên đen, 4 viên trắng, 5 viên xanh, 4 viên đen, 4 viên trắng,... Cứ tiếp tục như vậy. Hỏi màu của viên thứ 321 là màu gì? Màu của viên thứ 508 là màu gì?

Xem thêm các dạng Toán lớp 5 hay có trong đề thi vào lớp 6 chọn lọc, hay khác:

• Các bài toán về số tự nhiên và chữ số có lời giải

• Các bài toán về trung bình cộng có lời giải

• Các bài toán Tìm hai số khi biết tổng và hiệu có lời giải

• Các dạng toán có lời văn về phân số có lời giải

• Các bài toán về dãy số viết theo quy luật có lời giải

---