Cách giải các bài toán về chu vi và diện tích các hình (Ôn thi vào lớp 6)
Cách giải các bài toán về chu vi và diện tích các hình (Ôn thi vào lớp 6)
Nhằm mục đích giúp học sinh nắm vững được cấu trúc và các dạng toán hay có trong đề thi vào lớp 6 môn Toán, VietJack biên soạn tài liệu Cách giải các bài toán về chu vi và diện tích các hình đầy đủ phương pháp giải, ví dụ minh họa và bài tập tự luyện giúp học sinh ôn luyện và đạt điểm cao trong kì thi tuyển sinh vào lớp 6 môn Toán.
I. CÁC DẠNG TOÁN
Dạng 1. Tính chu vi và diện tích các hình
1. Phương pháp
Áp dụng công thức tính chu vi và diện tích các hình.
Đưa bài toán về các dạng toán quen thuộc: Tổng – hiệu; Tổng – tỉ; Hiệu – tỉ; Tỉ số; …
2. Ví dụ
Ví dụ 1. Một hình chữ nhật có chu vi 160m, nếu cắt chiều dài đi 8m và kéo chiều rộng thêm 8m thì hình mới là hình vuông. So sánh:
a) Chu vi hình chữ nhật và chu vi hình vuông.
b) Diện tích hình vuông và diện tích hình chữ nhật.
Bài giải
a) Cắt chiều dài đi 8 m và kéo chiều rộng thêm 8 m thì hình chữ nhật trở thành hình vuông. Lúc này chu vi hình vuông bằng chu vi hình chữ nhật (cùng thêm và bớt một số đơn vị vào một số).
b)
Cạnh hình vuông mới là:
160: 4 = 40 (m)
Diện tích của hình vuông là:
40 × 40 = 1600 (m2)
Chiều dài hình chữ nhật là:
40 + 8 =48 (m)
Chiều rộng hình chữ nhật là:
40 – 8 = 32 (m)
Diện tích hình chữ nhật là:
48 × 32 = 1536 (m2)
Diện tích hình vuông lớn hơn diện tích hình chữ nhật.
Ví dụ 2. Một hình chữ nhật có chiều dài gấp rưỡi chiều rộng và chu vi bằng 180m. Người ta kéo chiều dài thêm 5m. Phải kéo dài chiều rộng thêm bao nhiêu mét để được một hình vuông?
Bài giải
Tổng chiều dài và chiều rộng là:
180 : 2 = 90 (m)
Chiều dài gấp rưỡi chiều rộng nghĩa là chiều dài bằng 3/2 chiều rộng.
Ta có sơ đồ sau:
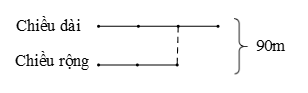
Chiều dài hình chữ nhật là:
90:(3+2)x3=54 (m)
Chiều rộng là:
90-54=36 (m)
Nếu chiều dài tăng thêm 5m thì chiều rộng phải tăng thêm 54+5-36=23 (m) để hình chữ nhật trở thành hình vuông.
Ví dụ 3. Cho hình chữ nhật ABCD có diện tích là 2400cm2. Trên AD lấy điểm M sao cho AM = 15cm, DM = 25cm. Tính diện tích tam giác MDC.
Bài giải
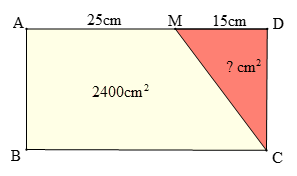
Độ dài cạnh AD là:
25 + 15 = 40 (cm)
Diện tích của hình chữ nhật ABCD là 2400cm2.
Độ dài cạnh CD là:
2400 : 40 = 60 (cm)
Diện tích tam giác MDC là:
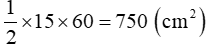
Đáp số: 750cm2
Ví dụ 4. Cho hình tròn tâm O. Hai đường kính AB và CD vuông góc với nhau. Nối AC, CB, BD và DA.
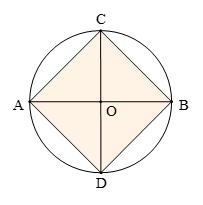
Tính diện tích phần không được tô màu theo diện tích của hình tròn tâm O.
Bài giải
Gọi r là bán kính của đường tròn tâm O.
Diện tích hình vuông ACBD là: r × r × 2
Diện tích hình tròn tâm O là: r × r × 3,14
Diện tích phần không được tô màu là:
r × r × 3,14 - r × r × 2 = r × r × 1,14
Diện tích phần không được tô màu theo diện tích của hình tròn tâm O là:
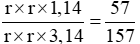
Vậy diện tích phần không được tô màu bằng 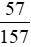 diện tích của hình tròn tâm O.
diện tích của hình tròn tâm O.
II. BÀI TẬP VỀ TỈ LỆ CHU VI VÀ DIỆN TÍCH CÁC HÌNH
Ví dụ 1. Cho tam giác ABC. Trên cạnh BC lấy điểm I, sao cho IB = IC. Nối AI, trên đoạn AI lấy điểm M để có 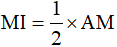 . Nối và kéo dài đoạn CM cắt cạnh AB tại N. So sánh diện tích 2 hình tam giác AMN và BMN.
. Nối và kéo dài đoạn CM cắt cạnh AB tại N. So sánh diện tích 2 hình tam giác AMN và BMN.
Bài giải
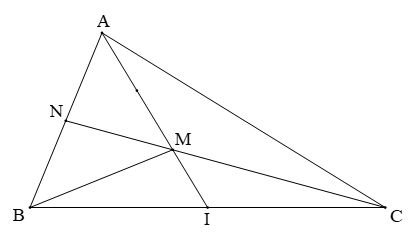
Vì hai tam giác MIC và MIA có cùng đường cao kẻ từ C và  nên
nên 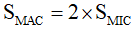 .
.
Vì hai tam giác MIC và MIB có cùng đường cao kẻ từ M và IB = IC nên 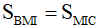 .
.
Mà 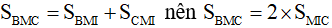
Suy ra 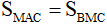 .
.
Ta lại có, hai tam giác MAC và BMC có chung đáy MC nên hai tam giác MAC và BMC có đường cao bằng nhau.
Suy ra, hai tam giác ANM và BNM có đường cao bằng nhau.
Tam giác ANM và tam giác BNM có đường cao bằng nhau và chung đáy MN nên 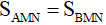 .
.
Vậy 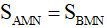 .
.
Ví dụ 2. Cho hình vẽ:
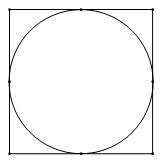
Biết diện tích hình tròn là 251,2cm2. Tính diện tích hình vuông.
Bài giải:
Giả sử bán kính của hình tròn là r (cm).
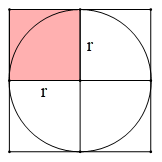
Ta có:
r × r × 3,14 = 251,2
r × r = 80
r × r là diện tích của hình vuông được tô màu mà diện tích hình vuông được tô màu bằng 1/4 diện tích hình vuông lớn.
Diện tích hình vuông lớn là: 80 × 4 = 320 (cm2)
Đáp số:
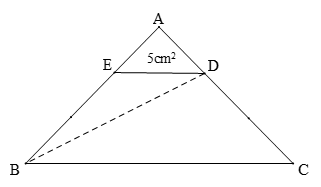
Ví dụ 3. Cho hình tam giác ABC. Trên cạnh AB ta lấy điểm E sao cho BE gấp đôi AE, trên cạnh AC ta lấy điểm D sao cho CD gấp đôi AD. Nối E với D ta được hình tam giác AED có diện tích 5 cm2. Hãy tính diện tích hình tứ giác BCDE.
Bài giải
Vì 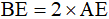 nên
nên 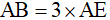 và
và 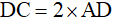 nên
nên 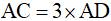 .
.
Vì tam giác ABD và tam giác AED có cùng đường cao và nên 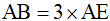 .
.
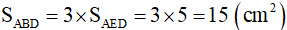
Vi tam giác ABD và tam giác ABC có cùng đường cao và nên 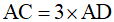 .
.
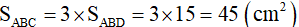
Ta có:
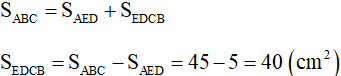
Vậy tính diện tích hình tứ giác BCDE bằng 40cm2.
III. BÀI TẬP VẬN DỤNG
Bài 1. Cho một hình chữ nhật có diện tích bằng 1080cm2. Biết nếu giảm chiều rộng đi 4cm thì diện tích hình chữ nhật giảm đi 180cm2. Tính chu vi hình chữ nhật.
Bài 2. Cho một hình chữ nhật, biết nếu tăng chiều dài, chiều rộng mỗi chiều thêm 2cm thì diện tích hình chữ nhật tăng thêm 50cm2. Chu vi hình chữ nhật đã cho là … cm.
Bài 3. Cho một hình chữ nhật, biết nếu giảm chiều dài, chiều rộng mỗi chiều thêm 5cm thì diện tích hình chữ nhật đã cho giảm đi 150cm2. Tính chu vi của hình chữ nhật đã cho.
Bài 4. Một hình chữ nhật có chu vi bằng 5 lần chiều rộng. Biết chiều dài bằng 60m. Tìm chiều rộng của hình chữ nhật.
Bài 5. Cho một hình bình hành có diện tích bằng 900cm2 , biết nếu giảm chiều cao đi 6cm thì diện tích hình bình hành giảm còn 720cm2. Tính độ dài đáy của hình bình hành.
Bài 6. Một hình thoi có hiệu độ dài hai đường chéo bằng 17/46 dm, độ dài đường chéo thứ nhất bằng 2/3 độ dài đường chéo thứ hai. Tính diện tích hình thoi.
Bài 7. Một hình thoi có độ dài đường chéo thứ nhất là 20m, độ dài đường chéo thứ hai bằng 1/2 độ dài đường chéo thứ nhất. Một hình vuông có diện tích bằng diện tích hình thoi. Tính cạnh hình vuông.
Bài 8. Một hình bình hành có độ dài đáy là 8dm, chiều cao là 3dm. Một hình thoi có diện tích bằng diện tích của hình bình hành này, có độ dài một đường chéo là 6dm. Tìm độ dài đường chéo còn lại.
Bài 9. Cho tam giác ABC có BC = 8 cm. Trên cạnh AC lấy điểm chính giữa D. Nối B với D. Trên BD lấy điểm E sao cho BE gấp đôi ED. Nối AE, kéo dài cắt BC ở M. Tính độ dài đoạn BM.
Bài 10. Một hình chữ nhật có chiều dài gấp 4 lần chiều rộng. Nếu tăng chiều rộng thêm 45 m thì được hình chữ nhật mới có chiều dài vẫn gấp 4 lần chiều rộng. Tính diện tích hình chữ nhật ban đầu.
Bài 11. Cho hình thang ABCD như hình bên. Biết diện tích 2 tam giác AED và BCF lần lược bằng 5,2cm2 và 4,8cm2. Tính diện tích hình tứ giác MFNE.
Bài 12. Cho tứ giác ABCD, M là điểm ở trên cạnh AB sao cho 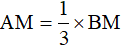 . Tính diện tích tam giác MCD biết rằng diện tích tam giác ACD và tam giác BCD tương ứng là 24cm2 và 16cm2.
. Tính diện tích tam giác MCD biết rằng diện tích tam giác ACD và tam giác BCD tương ứng là 24cm2 và 16cm2.
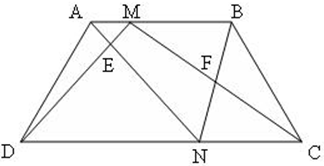
Bài 13. Cho hình thang ABCD có đáy nhỏ 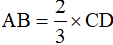 . AC và BD cắt nhau tại O. Diện tích hình tam giác BOC là 15cm2. Tính diện tích hình thang ABCD ?
. AC và BD cắt nhau tại O. Diện tích hình tam giác BOC là 15cm2. Tính diện tích hình thang ABCD ?
Bài 14. Cho tam giác ABC có BC = 8 cm. Trên cạnh AC lấy điểm chính giữa D. Nối B với D. Trên BD lấy điểm E sao cho BE gấp đôi ED. Nối AE, kéo dài cắt BC ở M. Tính độ dài đoạn BM.
Bài 15. Cho hình thang vuông ABCD, AD = 6cm, DC = 12cm, 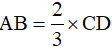 .
.
a) Tính diện tích hình thang ABCD.
b) Kéo dài cạnh bên AD và CB, chúng gặp nhau tại M . Tính độ dài cạnh AM.
Xem thêm các dạng Toán lớp 5 hay có trong đề thi vào lớp 6 chọn lọc, hay khác:
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

