Tài liệu môn Toán lớp 5 hay, chi tiết năm 2021

Siêu sale 5-5 Shopee

Tài liệu môn Toán lớp 5 hay, chi tiết năm 2021

Bộ tài liệu môn Toán lớp 5 đầy đủ các dạng bài tập có trong đề thi vào lớp 6 môn Toán và bộ đề thi Toán vào lớp 6 có đáp án được tổng hợp từ các trường THCS trên cả nước nhằm mục đích giúp Giáo viên, phụ huynh có thêm tài liệu môn Toán lớp 5 để giúp học sinh ôn luyện và đạt điểm cao trong kì thi tuyển sinh vào lớp 6.

Các dạng Toán ôn thi vào lớp 6 chọn lọc

Bộ đề thi vào lớp 6 môn Toán

Các bài toán về Tỉ số phần trăm có lời giải

I. Các dạng toán

Dạng 1. Tìm tỉ số phần trăm của hai số

1. Phương pháp

Để tìm tỉ số phần trăm của số A so với số B ta chia số A cho số B rồi nhân với 100.

2. Ví dụ

Ví dụ 1. Một lớp học có 28 em, trong đó có 7 em học giỏi toán. Hãy tìm tỉ số phần trăm học sinh giỏi toán so với sĩ số của lớp?

Bài giải

Tỉ số phần trăm học sinh giỏi toán so với học sinh cả lớp là:
7 : 28 = 0,25 = 25%

Đáp số: 25%

Ví dụ 2. Trong vườn có 12 cây cam và 28 cây chanh. Tìm tỉ số phần trăm số cây cam so với số cây trong vườn?

Bài giải

Số cây trong vườn là:

12 + 28 = 40 (cây)

Tỉ số phần trăm số cây cam so với số cây trong vườn là:

12 : 40 = 0,3 = 30%

Đáp số: 30%

Dạng 2. Tìm giá trị phần trăm của một số

1. Phương pháp

Để tìm tỉ số phần trăm của số A so với số B ta chia số A cho số B rồi nhân với 100.

2. Ví dụ

Ví dụ 1. Chiếc xe đã đi được 40% chiều dài của con đường dài 250 km. Tính phần còn lại của con đường mà xe còn phải đi.

Bài giải

Xe đó đã đi được:

40% × 250 = 100 (km)

Phần còn lại của con đường mà xe còn phải đi là:

250 - 100 = 150 (km)

Đáp số: 150km

Ví dụ 2. Một cái xe đạp giá 400 000 đồng, nay hạ giá 15%. Hỏi giá cái xe đạp bây giờ là bao nhiêu?

Bài giải

Giá bán đã hạ bớt:

15% × 400 000 = 60 000 (đồng)

Giá xe đạp bây giờ là:

400 000 – 60 000 = 340 000 (đồng)

Đáp số: 340 000 đồng

Dạng 3. Tìm một số khi biết giá trị một số phần trăm của nó

1. Phương pháp

Muốn tìm giá trị phần trăm của một số ta lấy số đó chia cho 100 rồi nhân với số phần trăm hoặc lấy số đó nhân với số phần trăm rồi chia cho 100.

2. Ví dụ

Ví dụ 1. Số học sinh giỏi của một trường tiểu học là 64 em chiếm 12,8% số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh?

Bài giải

1% học sinh của trường là:

64 : 12,8% = 5 (học sinh)

Số học sinh toàn trường là:

5 × 100 = 500 (học sinh)

C2.

Trường đó có số học sinh là:

64 : 12,8 × 100 = 500 (học sinh)

Đáp số: 500 học sinh

Ví dụ 2. Khi trả bài kiểm tra toán của lớp 5A, cô giáo nói: "Số điểm 10 chiếm 25%, số điểm 9 ít hơn 5%". Biết rằng có tất cả 18 điểm 9 và 10. Hỏi lớp 5A có bao nhiêu bạn?

Bài giải

Tỉ số phần trăm số bạn điểm 9 là:

25% - 5% = 20%

Tỉ số phần trăm học sinh đạt điểm 9 và 10 so với số học sinh cả lớp là:

25% + 20% = 45%

1% số học sinh của lớp là:

18 : 45% = 0,4 (bạn)

Sĩ số lớp là:

0,4 × 100 = 40 (bạn)

Đáp số: 40 bạn

Dạng 4. Bài toán về tính lãi

1. Phương pháp

- Đọc đề bài và xác định tiền vốn (giá mua), giá bán, tiền lãi, tiền lỗ.

- Áp dụng công thức:

Giá bán = Giá mua + Lãi

Giá bán = Giá mua – Lỗ

2. Ví dụ

Ví dụ 1. Một cửa hàng định giá mua hàng bằng 75% giá bán. Hỏi cửa hàng đó định giá bán bằng bao nhiêu phần trăm giá mua?

Bài giải

Xem giá bán là 100% thì giá mua là 75%.

Vậy giá bán ra so với giá mua vào chiếm số phần trăm là:

100 : 75 = 133,33%

Đáp số: 133,33% giá mua

Ví dụ 2. Một chiếc xe đạp giá 1 700 000 đồng, nay hạ giá 15%. Hỏi giá chiếc xe đạp bây giờ là bao nhiêu?

Bài giải

Xem giá chiếc xe đạp lúc đầu là 100%, sau khi giảm chỉ còn:

100% – 15% = 85%

Giá chiếc xe đạp hiện nay là:

1 700 000 × 85 : 100 = 1 445 000(đồng)

Đáp số: 1 445 000 đồng.

Ví dụ 3. Một cửa hàng sách, hạ giá 20% giá sách nhân ngày 20/11. Tuy vậy, cửa hàng vẫn còn lãi 8%. Hỏi, ngày thường (không hạ giá) thì cửa hàng được lãi bao nhiêu phần trăm?

Bài giải

Coi giá bán ngày thường là 100% thì giá bán ngày 20/11 là:

100% - 20% = 80%

Cửa hàng vẫn còn lãi 8% tức là cửa hàng bán được:

100% + 8% = 108% (giá mua)

Số tiền lãi tính theo giá mua là:

100 : 80 × 108 = 135% (giá mua)

Vậy ngày thường thì cửa hàng lãi được:

135% - 100% = 35%

Đáp số: 35%

Dạng 5. Bài toán đưa về dạng toán quen thuộc

1. Phương pháp

Đưa về các dạng toán quen thuộc như tổng – tỉ, hiệu – tỉ, …

2. Ví dụ

Ví dụ 1. Tổng của hai số bằng 25% thương của hai số đó cũng bằng 25%. Tìm hai số đó.

Bài giải

Đổi: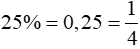

Ta có sơ đồ:

Số thứ nhất là: 0,25 : (1+4) = 0,05

Số thứ hai là: 0,25 – 0,05 = 0,2

Đáp số: 0,05 và 0,2

Ví dụ 2. Tìm hai số, biết 25% số thứ nhất bằng 1/3 số thứ hai và hiệu của hai số là 15/37.

Bài giải

Đổi: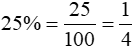

Theo bài ra, 1/4 số thứ nhất bằng 1/3 số thứ hai. Ta có sơ đồ:

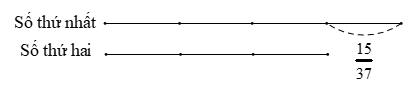
Số thứ nhất là:

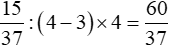
Số thứ hai là:

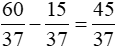
Đáp số: 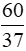và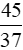

II. Bài tập vận dụng

Bài 1. Lớp 5A có 46 học sinh. Tỉ số phần trăm giữa số học sinh nam và số học sinh nữ lớp đó là 100%. Lớp đó có bao nhiêu học sinh nam? Bao nhiêu học sinh nữ?
Bài 2. Giá bán 1kg gạo hôm qua là 16000 đồng. Hôm nay giá gạo giảm 10%. Hỏi hôm nay mua 10kg gạo phải trả bao nhiêu tiền?

Bài 2. Tăng mỗi cạnh của hình chữ nhật thêm 20% số đo của nó thì diện tích hình chữ nhật tăng thêm bao nhiêu phần trăm?
Bài 4. Số gạo tẻ trong kho bằng 120% số gạo nếp. Hỏi phải bán bao nhiêu phần trăm số gạo tẻ để số gạo còn lại của hai loại gạo bằng nhau.
Bài 5. Lãi suất tiết kiệm là 0,65%/tháng. Để sau một tháng nhận được tiền lãi là 832000 đồng thì khách hàng phải gửi số tiền gốc là bao nhiêu?
Bài 6. Một cửa hàng bán một chiếc ti vi giá 9600000 đồng, như vậy lãi 20% so với giá nhập chiếc ti vi đó. Hỏi cửa hàng đã nhập chiếc ti vi đó giá bao nhiêu?
Bài 7. Diện tích thửa ruộng thứ nhất bằng 5/6 diện tích thửa ruộng thứ hai. Hỏi tỉ số phần trăm giữa diện tích thửa ruộng thứ hai và thửa ruộng thứ nhất là bao nhiêu?
Bài 8. Một hình chữ nhật có chiều dài 48cm, chiều rộng 30cm. Tính tỉ số phần trăm của chiều dài so với chiều rộng.
Bài 9. Lớp 5A có 45 học sinh. Số học sinh nữ chiếm 60% số học sinh cả lớp. Hỏi số học sinh nam lớp đó là bao nhiêu em?
Bài 10. Tăng chiều dài 20% số đo của nó, đồng thời giảm chiều rộng 20% số đo của nó thì diện tích hình chữ nhật đó thay đổi thế nào?

Bài 3. Lớp 5A có 45 học sinh trong đó có 18 học sinh nữ. Tính tỉ số phần trăm của số học sinh nam so với số học sinh nữ.

Bài 4. Một người bán chiếc quạt với giá 375000 đồng thì được lãi 12% so với giá bán. Hỏi để lãi 15% so với giá gốc thì phải bán chiếc quạt đó giá bao nhiêu?
Bài 13. Lớp 5A có 45 học sinh, trong đó có 18 học sinh nam. Hỏi số học sinh nữ bằng bao nhiêu phần trăm số học sinh nam?
Bài 14. Một người bán một món hàng với giá 407000 đồng thì được lãi 10% so với giá gốc. Hỏi để lãi 15% so với giá gốc thì người ta phải bán món hàng đó với giá bao nhiêu?
Bài 15. Phải đổ thêm bao nhiêu gam muối vào một bình đựng 300g dung dịch 2% muối để nhận được một bình đựng dung dịch 4% muối.
Bài 16. Sau khi giảm giá 25% thì giá một chiếc xe đạp là 757500 đồng. Hỏi ban đầu giá một chiếc xe đạp là bao nhiêu?
Bài 17. Một cửa hàng bán lương thực đã bán được 20% số gạo trong kho. Hỏi phải nhập thêm bao nhiêu phần trăm số gạo còn lại để trong kho vẫn có số gạo như lúc đầu có?
Bài 18. Một cửa hàng định giá mua bằng 75% giá bán. Hỏi nếu cửa hàng mua một mặt hàng với giá 4500000 đồng thì sẽ bán mặt hàng đó với giá bao nhiêu?
Bài 19. Một hình tam giác có cạnh đáy bằng chiều dài hình chữ nhật, chiều cao bằng 1/2 chiều rộng hình chữ nhật đó. Hỏi diện tích hình tam giác bằng bao nhiêu phần trăm diện tích hình chữ nhật?

Bài 5. Một cửa hàng niêm yết giá bán một chiếc ti vi là 13400000 đồng. Nếu bán chiếc ti vi này bằng 50% giá niêm yết thì lãi 25% so với tiền vốn. Hỏi phải bán chiếc ti vi đó với giá bao nhiêu thì được lãi 50% so với tiền vốn?

Các bài toán công việc chung – công việc riêng có lời giải

I. CÁC DẠNG BÀI

Dạng 1. Biết thời gian làm riêng một công việc, yêu cầu tìm thời gian làm công việc chung đó.

1. Phương pháp

Bước 1. Quy ước một đại lượng (như công việc cần hoàn thành, quãng đường cần đi, thể tích của bể nước,…) là đơn vị.

Bước 2. Tính số phần công việc làm riêng trong một giờ.

Bước 3. Tính số phần công việc làm chung trong một giờ.

Bước 4. Tính thời gian làm chung để hoàn thành công việc đó.

2. Ví dụ

Ví dụ 1. Hai người thợ nhận làm chung một công việc. Người thợ thứ nhất làm một mình thì hoàn thành công việc trong 4 giờ. Người thợ thứ hai làm một mình thì hoàn thành công việc trong 6 giờ. Hỏi cả hai người cùng làm thì hoàn thành công việc đó mất bao lâu?

Bài giải

Trong 1 giờ người thợ thứ nhất làm một mình được:

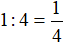(công việc)

Trong 1 giờ người thợ thứ hai làm một mình được:

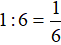(công việc)

Trong 1 giờ cả hai người cùng làm được:

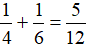(công việc)

Thời gian để hai người cùng làm chung hoàn thành xong công việc đó là:

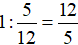(giờ) = 2 giờ 24 phút

Đáp số: 2 giờ 24 phút

Ví dụ 2. Người thứ nhất đi từ A đến B hết 7 giờ. Người thứ hai đi từ B về A thì hết 5 giờ. Hỏi nếu cùng một lúc, người thứ nhất đi từ A và người thứ hai đi từ B thì sau bao lâu họ gặp nhau?

Bài giải

Ta quy ước quãng đường AB là đơn vị.

Trong 1 giờ người thứ nhất đi được:

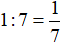(quãng đường AB)

Trong 1 giờ người thứ hai đi được:

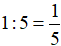(quãng đường AB)

Trong 1 giờ cả hai người cùng đi người thứ nhất đi từ A đến B và người thứ hai đi từ B về A thì đi được:

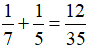(quãng đường AB)

Thời gian cả hai người cùng đi đến lúc họ gặp nhau là:

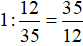(giờ) = 2 giờ 55 phút

Đáp số: 2 giờ 55 phút

Ví dụ 3. Một cái hồ có 3 vòi nước: hai vòi cùng cháy nước vào và một vòi tháo nước ra. Biết rằng vòi thứ nhất chảy một mình mất 8 giờ thì đấy hồ, vòi thứ hai chảy một mình mất 6 giờ thì đầy hồ, vòi thứ ba tháo ra một mình mất 4 giờ thì hồ cạn. Hồ đang cạn, nếu mở cả 3 vòi cùng một lúc thì mất bao hồ đầy?

Bài giải:

Ta quy ước thể tích của hồ nước là đơn vị.

Trong 1 giờ vòi thứ nhất chảy vào được:

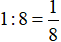(hồ nước)

Trong 1 giờ vòi thứ hai chảy vào được:

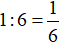(hồ nước)

Trong 1 giờ vòi thứ ba tháo ra hết:

(hồ nước)

Trong 1 giờ cả 3 vòi cùng chảy thì lượng nước trong hồ tăng lên:

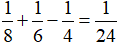(hồ nước)

Thời gian cả 3 vòi cùng chảy đầy hồ là:

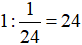(giờ)

Đáp số: 24 giờ

Dạng 2. Biết thời gian cùng chung hoàn thành xong công việc và thời gian làm riêng (đã biết). Hoàn thành xong công việc đó, yêu cầu tính thời gian là riêng (chưa biết) xong công việc đó.

1. Phương pháp

Bước 1. Quy ước đại lượng không đổi là đơn vị.

Bước 2. Tính số phần công việc làm chung trong 1 giờ (bằng cách lấy đơn vị chia cho thời gian làm chung công việc đó).

Bước 3. Tính số phần công việc làm riêng (đã biết thời gian làm riêng ) trong 1giờ (bằng cách lấy đơn vị chia cho thời gian làm riêng công việc đó).

Bước 4. Tính số phần công việc làm riêng trong 1 giờ (bằng cách lấy số phần công việc làm – công việc đó- trong 1giờ trừ đi số phâng công việc làm riêng – công việc đó- trong 1 giờ)

Bước 5. Tính thời gian làm riêng hoàn thành công việc (bằng cách lấy đơn vị chia cho số phần công việc làm riêng trong 1 giờ).

2. Ví dụ

Ví dụ 1. Hai người cúng là chung một công việc thì sau 5 giờ sẽ xong. Nếu một mình người thợ cả làm thì phải làm 8 giờ mới xong. hỏi người thợ thứ hai làm một mình sau bao lâu sẽ xong công việc đó?

Bài giải:

Ta quy ước công việc cần xong là đơn vị.

Trong 1 giờ cả hai người thợ cùng làm được:

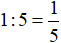(công việc)

Trong 1 giờ người thợ cả làm được:

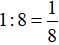(công việc)

Trong 1 giờ người thợ thứ hai làm được:

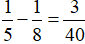(công việc)

Thời gian người thợ thứ hai làm một mình xong công việc đó là:

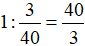(giờ) = 13 giờ 20 phút

Đáp số: 13 giờ 20 phút

Ví dụ 2. Cả ba vòi nước cùng chảy vào một cái bể sau 3 giờ thì đầy bể. Nếu vòi thứ nhất chảy một mình thì phải mất 8 giờ mới đầy bể. Nếu vòi thứ hai chảy một mình thì phải mất 12 giờ mới đầy bể. Hỏi vòi thứ ba chảy một mình thì phải mất bao lâu mới đầy bể?

Bài giải

Ta quy ước thể tích của bể là đơn vị.

Trong 1 giờ cả ba vòi cùng chảy được:

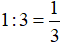(bể nước)

Trong 1 giờ vòi thứ nhất chảy được:

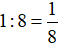(bể nước)

Trong 1 giờ vòi thứ hai chảy được:

(bể nước)

Trong 1 giờ cả vòi thứ nhất và vòi thứ hai cùng chảy được:

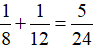(bể nước)

Trong 1 giờ vòi thứ ba chảy được:

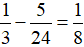(bể nước)

Thời gian thời vòi thứ ba chảy một mình đầy bể là:

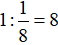(giờ)

Đáp số: 8 giờ

Dạng 3. Cho thời gian làm riêng công việc và tổng thời gian hai người làm liên tiếp để xong công việc, yêu cầu tính thời gian mỗ người làm (kiểu nay thường phối hợp nhiều phương pháp giải).

1. Phương pháp

Bước 1. Quy ước đại lượng không đổi là đơn vị.

Bước 2. Tính số phần công việc người thứ nhất làm trong 1 giờ

Bước 3. Tính số phần công việc người thứ hai làm trong 1 giờ

Bước 4. Giả sử thời gian hoàn thành công việc khi làm riêng của người thứ hai bằng thời gian cả hai người hoàn thành công việc.

Bước 5. Tính số phần công việc mỗi giờ người thứ nhất làm nhiều hơn người thứ hai (hoặc ngược lại)

Bước 6. Tính thời gian người thứ nhất làm; Tính thời gian người thứ hai làm.

2. Ví dụ

Có một công việc, nếu Sơn làm một mình thì hết 10 giờ; nếu Dương làm một mình thì hết 15 giờ. Lúc đầu, Sơn làm rồi nghỉ sau đó Dương làm tiếp cho đến khi xong việc. Hai bạn làm hết 11 giờ. Hỏi mỗi bạn làm trong mấy giờ?

Bài giải

Ta quy ước công việc cần xong là đơn vị.

Mỗi giờ Sơn làm được số phần công việc là:

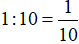(công việc)

Mỗi giờ Dương làm được số phần công việc là:

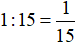(công việc)

Giả sử Dương làm một mình trong cả 11 giờ thì làm được số phần công việc là

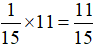(công việc)

Khi đó số phần công việc còn lại chưa làm xong là:

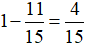(công việc)

Sở dĩ có phần công việc chưa làm xong là do ta thấy số giờ Sơn làm bằng số giờ Dương làm.

Mỗi giờ Sơn làm được nhiều hơn Dương là:

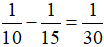(công việc)

Thời gian Sơn làm là:

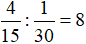(giờ)

Thời gian Dương làm là:

11 – 8 = 3 (giờ)

Đáp số: Sơn 8 giờ; Dương 3 giờ

II. BÀI TẬP VẬN DỤNG

Bài 1. Hai người cùng đắp một nền nhà thì phải mất 4 ngày mới xong. Nếu một mình người thứ nhất đắp thì phải mất 6 ngày mới xong. Hỏi nếu một mình người thứ hai đắp thì phải mất mấy ngày mới xong?

Bài 2. An và Toàn nhận làm chung một công việc. Nếu một mình An làm thì sau 4 giờ sẽ xong, còn nếu một mình Toàn làm thì sau 6 giờ sẽ xong. Hỏi nếu cả hai bạn cùng làm thì xong công việc trong bao lâu?

Bài 3. Ba người thợ cùng làm chung một công việc. Nếu làm một mình thì người thứ nhất phải mất 3 giờ, người thứ hai phải mất 4 giờ, người thứ ba phải mất 6 giờ mới xong. Hỏi cả ba người cùng làm thì sẽ hoàn thành công việc trong bao lâu?

Bài 4. Bác Thành hoàn thành một công việc phải mất 3 giờ, bác Mai hoàn thành công việc đó phải mất 4 giờ. Hỏi hai bác cùng làm thì phải mất bao nhiêu lâu mới xong công việc đó?

Bài 5. A và B cùng hoàn thành một công việc phải mất 3 giờ. B và C cùng hoàn thành công việc đó phải mất 4 giờ. C và A cùng hoàn thành công việc đó phải mất 2 giờ rưỡi. Hỏi cả ba người cùng làm thì mất bao lâu sẽ xong công việc?

Bài 6. Ở một cái bể có hai vòi nước. Vòi thứ nhất chảy vào đầy bể sau 5 giờ, vòi thứ

hai chảy vào đầy bể sau 7 giờ. Nếu bể không có nước, mở cả hai vòi cùng một lúc

thì sau bao lâu sẽ đầy bể.

Bài 7. Ba vòi nước cùng chảy vào một cái bể không có nước. Nếu vòi I và vòi II cùng chảy thì đầy bể trong 6 giò. Nếu vòi II và vòi III cùng chảy thì đầy bể trong 8 giờ. Nếu vòi I và vòi III cùng chảy thì đầy bể trong 12 giờ. Hỏi chỉ một mình vòi III chảy thì đầy bể sau bao lâu?

Bài 8. Ở một cái bể có hai vòi nước, vòi 1 chảy vào và vòi 2 tháo ra. Nếu bể cạn vòi thứ nhất chảy vào đầy bể sau 5 giờ. Nếu bể đầy nước vòi thứ hai sẽ tháo ra cạn bể sau 7 giờ. Hiện tại bể không có nước, mở cả hai vòi nước cùng một lúc thì bao lâu đầy bể?

Bài 9. Một bể có 3 vòi nước: hai vòi chảy vào và một vòi chảy ra. Biết rằng vòi thứ nhất chảy 6 giờ thì đầy bể, vòi thứ hai chảy 4 giờ thì đầy bể, vòi thứ ba tháo ra 8 giờ thì cạn bể. Bể đang cạn, nếu mở cả 3 vòi cùng một lúc thì sau bao lâu bể đầy?

Bài 10. Ở một cái bể có hai vòi A và B chảy vào, vòi C tháo nước ra. Một mình vòi A chảy vào đầy bể sau 6 giờ, một mình vòi B chay vào đầy bể sau 5 giờ. Nếu bể đầy nước mở vòi C thì sau 3 giờ bể cạn. Giả sử bể không có nước, mở 3 vòi cùng một lúc, hỏi sau bao lâu bể đầy nước?

Bài 11. Thành và Tâm cùng làm chung một công việc thì phải mất 7 giờ mới xong. Nhưng sau khi hai người đã làm chung được 5 giờ thì Thành bị ốm phải nghỉ chỉ còn mình Tâm làm nên Tâm phải làm trong 6 giờ nữa mới xong. Hỏi nếu mỗi người chỉ làm một mình thì mất mấy giờ mới xong công việc đó?

Bài 12. Ba người cùng làm chung một công việc thì xong trong 6 giờ. Nếu người thứ nhất làm một mình thì xong trong 12 giờ, người thứ hai làm một mình thì xong trong 15 giờ. Hỏi người thứ ba nếu làm một mình thì xong công việc đó trong bao lâu?

Bài 13. Một người làm một công việc thì xong trong 12 giờ. Sau khi làm được 6 giờ thì có người thứ hai đến cùng làm và cả hai người đã làm xong phần còn lại trong 1 giờ 30 phút. Hỏi nếu người thứ hai làm một mình thì xong công việc trong bao lâu?

Bài 14. Ba người cùng làm chung một công việc thì xong trong 10 giờ, nhưng khi làm thì có một người phải chuyển đi làm việc khác nên 2 người còn lại phải làm trong 15 giờ mới xong. Hỏi nếu một mình người chuyển đi làm thì phải trong bao lâu mới xong việc?

Bài 15. Để làm xong một công việc, tổ một phải làm trong 9 giờ, tổ hai phải làm trong 12 giờ. Khi tổ một làm được 6 giờ thì phải chuyển đi làm việc khác để tổ hai làm tiếp cho đến khi xong. Hỏi tổ hai phải làm xong công việc đó trong bao lâu?

Bài 16. Người thứ nhất một mình có thể hoàn thành một công việc trong 25 ngày, người thứ hai trong 20 ngày, người thứ ba trong 24 ngày. Cả ba người cùng làm trong 2 ngày , sau đó chỉ còn người thứ ba làm tiếp trong 6 ngày rồi người thứ nhất trở lại cùng với một người thứ tư và cả ba người cùng làm thêm 4 ngày nữa thì xong công việc. Hỏi nếu một mình người thứ tư làm thì phải bao nhiêu ngày mới làm xong toàn bộ công việc?

Bài 17. Hai vòi nước cùng chảy vào một cái bể không có nước sau 6 giờ sẽ đầy bể. Nếu vòi I chảy một mình thì sau 10 giờ mới đầy bể. Hỏi nếu vòi II chảy riêng một mình thì sau bao lâu sẽ đầy bể?

Bài 18. Hai vòi nước cùng chảy vào một bể không chứa nước thì sau 3 giờ sẽ đầy bể. Nếu cho hai vòi cùng chảy vào bể không chứa nước trong 2 giờ, sau đó tắt vòi thứ nhất thì vòi thứ hai chảy thêm 3 giờ nữa sẽ đầy bể. Hỏi nếu chảy riêng vào bể không chứa nước thì mỗi vòi chảy đầy bể trong bao lâu?

Bài 19. Một con trâu ăn hết một bó cỏ trong 16 phút. Nhưng trâu mới ăn được 4 phút thì có thêm một con bê đến ăn cùng. Cả hai ăn trong 10 phút nữa thì hết cỏ. Hỏi nếu con bê ăn một mình thì sau bao lâu hết bó cỏ?

Bài 20. Ba người cùng làm một công việc sẽ xong trong 2 giờ 40 phút. Nếu làm riêng một mình thì người thứ nhất phải mất 8 giờ mới xong công việc, người thứ hai phải mất 12 giờ mới xong công việc. Hỏi nếu người thứ ba làm một mình thì phải mất bao lâu mới xong công việc?

Sách VietJack thi THPT quốc gia 2024 cho học sinh 2k6:

Săn shopee siêu SALE :

ĐỀ THI, GIÁO ÁN, GÓI THI ONLINE DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 12

Bộ giáo án, đề thi, bài giảng powerpoint, khóa học dành cho các thầy cô và học sinh lớp 12, đẩy đủ các bộ sách cánh diều, kết nối tri thức, chân trời sáng tạo tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official