Vận dụng trang 26 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 18: Phương trình quy về phương trình bậc hai

Vận dụng trang 26 Toán 10 Tập 2: Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4 km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở thôn Hoành, bên bờ biển cách bến Bính 9,25 km và sẽ được anh Nam vận chuyển trên con đường dọc bờ biển tới bến Bính bằng xe kéo. Bác Việt đã gọi điện thống nhất với anh Nam là họ sẽ gặp nhau ở vị trí nào đó giữa bến Bính và thôn Hoành để hai người có mặt tại đó cùng lúc, không mất thời gian chờ nhau. Giả thiết rằng đường dọc bờ biển là thẳng và bác Việt cũng di chuyển theo một đường thẳng để tới điểm hẹn. Tìm vị trí hai người hẹn gặp, biết rằng vận tốc của anh Nam là 5 km/h và của bác Việt là 4 km/h. 

Hướng dẫn 

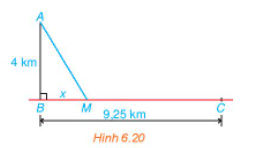
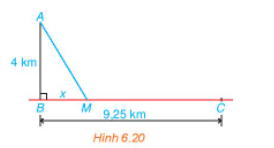
Ta mô hình hóa bài toán như trong Hình 6.20: Trạm hải đăng ở vị trí A; bến Bính ở B và thôn Hoành ở C. 

Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM = x (km) (x > 0). Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe nên ta có phương trình: 

$\frac{\sqrt{x^2+16}}{4}=\frac{\mathrm{9,25}-x}{5}$. 

Giải phương trình này sẽ tìm được vị trí hai người dự định gặp nhau. 

Lời giải:

Ta mô hình hóa bài toán như trong Hình 6.20: Trạm hải đăng ở vị trí A; bến Bính ở B và thôn Hoành ở C. 

Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM = x (km) (x > 0).

Ta có: BC = BM + MC ⇔ MC = BC – BM = 9,25 – x (km) hay quãng đường của anh Nam từ thôn Hoành đến điểm gặp nhau của 2 người là 9,25 – x (km). 

Vận tốc của anh Nam là 5 km/h nên thời gian di chuyển của anh Nam đến điểm hẹn gặp nhau là: $\frac{\mathrm{9,25}-x}{5}$(giờ). 

Tam giác ABC vuông tại B, theo định lí Pythagore ta có: 

AM² = AB² + BM² = 4² + x² = x² + 16 

Suy ra AM = $\sqrt{x^2+16}$(km) hay quãng đường di chuyển của bác Việt đến điểm hẹn là (km). 

Vận tốc của bác Việt là 4 km/h nên thời gian di chuyển của bác Việt tới điểm hẹn gặp nhau là: $\frac{\sqrt{x^2+16}}{4}$(giờ). 

Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe nên ta có phương trình: 

$\frac{\sqrt{x^2+16}}{4}=\frac{\mathrm{9,25}-x}{5}$(1). 

Giải phương trình trên ta có: 

(1)$\iff 5\sqrt{x^2+16}=37-4x$

Bình phương hai vế phương trình trên ta được:

25(x² + 16) = 1369 – 296x + 16x² 

⇔ 9x² + 296x – 969 = 0 

⇔ x = 3 hoặc x = $-\frac{323}{9}$

Thử lại ta thấy cả hai giá trị x = 3 và x = $-\frac{323}{9}$ đều thỏa mãn phương trình (1). 

 Mà điều kiện của x là x > 0 nên ta chọn x = 3. 

Vậy vị trí hai người hẹn gặp nhau cách bến Bính 3 km hay cách thôn Hoành 6,25 km.

Lời giải bài tập Toán 10 Bài 18: Phương trình quy về phương trình bậc hai hay, chi tiết khác:

• HĐ1 trang 25 Toán 10 Tập 2: Cho phương trình $\sqrt{x^2-3x+2}=\sqrt{-x^2-2x+2}$....

• Luyện tập 1 trang 25 Toán 10 Tập 2: Giải các phương trình sau: $\sqrt{3x^2-6x+1}=\sqrt{-2x^2-9x+1}$....

• HĐ2 trang 25 Toán 10 Tập 2: Cho phương trình $\sqrt{26x^2-63x+38}=5x-6$ ....

• Luyện tập 2 trang 26 Toán 10 Tập 2: Giải các phương trình sau: $\sqrt{2x^2+x+3}=1-x$....

• Bài 6.20 trang 27 Toán 10 Tập 2: Giải các phương trình sau: $\sqrt{3x^2-4x-1}=\sqrt{2x^2-4x+3}$....

• Bài 6.21 trang 27 Toán 10 Tập 2: Giải các phương trình sau: $\sqrt{6x^2+13x+13}=2x+4$ ....

• Bài 6.22 trang 27 Toán 10 Tập 2: Cho tứ giác ABCD có AB ⊥ CD; AB = 2; BC = 13; CD = 8; DA = 5 (H.6.21) ....

• Bài 6.23 trang 27 Toán 10 Tập 2: Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường ....

Các bài học để học tốt Toán 10 Bài 18: Phương trình quy về phương trình bậc hai:

• Giải SBT Toán 10 Bài 18: Phương trình quy về phương trình bậc hai

  Xem lời giải

• Lý thuyết Toán 10 Bài 18: Phương trình quy về phương trình bậc hai

  Xem chi tiết

• Trắc nghiệm Toán 10 Bài 18: Phương trình quy về phương trình bậc hai

  Xem chi tiết

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

• Toán 10 Bài 17: Dấu của tam thức bậc hai

• Toán 10 Bài tập cuối chương 6

• Toán 10 Bài 19: Phương trình đường thẳng

• Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

• Toán 10 Bài 21: Đường tròn trong mặt phẳng tọa độ

• Toán 10 Bài 22: Ba đường conic

Xem thêm các tài liệu học tốt lớp 10 hay khác:

• Giải sgk Toán 10 Kết nối tri thức
• Giải Chuyên đề học tập Toán 10 Kết nối tri thức
• Giải SBT Toán 10 Kết nối tri thức
• Giải lớp 10 Kết nối tri thức (các môn học)
• Giải lớp 10 Chân trời sáng tạo (các môn học)
• Giải lớp 10 Cánh diều (các môn học)

---