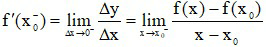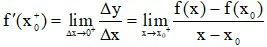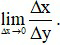Cách tính đạo hàm bằng định nghĩa hay, chi tiết
Bài viết Cách tính đạo hàm bằng định nghĩa hay, chi tiết sẽ giúp học sinh nắm vững lý thuyết, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 11.
Cách tính đạo hàm bằng định nghĩa (hay, chi tiết)
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
1. Lý thuyết
a) Định nghĩa đạo hàm
- Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a;b). Giới hạn hữu hạn (nếu có) của tỉ số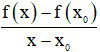 
khi x → x0 được gọi là đạo hàm của hàm số đã cho tại x0.
- Kí hiệu là f’(x0) hay y’(x0). Như vậy ta có: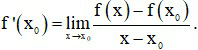
- Nhận xét:
Nếu đặt ∆x = x − x0 và ∆y = f(x0 + ∆x) − f(x0) thì ta có
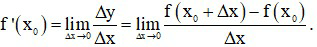
Trong đó ∆x được gọi là số gia của biến số tại x0
∆y gọi là số gia của hàm số ứng với số gia ∆x tại x0.
b) Đạo hàm một bên
- Đạo hàm bên trái của hàm số y = f(x) tại điểm x0, kí hiệu là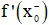 
được định nghĩa là:
trong đó x→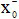 
được hiểu là x→ x0 và x < x0.
- Đạo hàm bên phải của hàm số y = f(x) tại điểm x0, kí hiệu là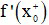 
được định nghĩa là:
trong đó x→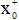 
được hiểu là x→ x0 và x > x0.
- Định lí: Hàm số y = f(x) có đạo hàm tại điểm x0 thuộc tập xác định của nó, nếu và chỉ nếu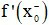 
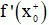
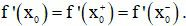
và 
tồn tại và bằng nhau. Khi đó ta có: 
c) Đạo hàm trên khoảng, trên đoạn
- Hàm số y = f(x) có đạo hàm (hay hàm khả vi) trên (a; b) nếu nó có đạo hàm tại mọi điểm thuộc (a; b).
- Hàm số y = f(x) có đạo hàm (hay hàm khả vi) trên [a; b] nếu nó có đạo hàm tại mọi điểm thuộc (a; b) đồng thời tồn tại đạo hàm trái f’(b -) và đạo hàm phải f’(a+) .
d) Quy tắc tính đạo hàm bằng định nghĩa
Muốn tính đạo hàm của hàm số tại điểm x0 theo định nghĩa, ta có 2 cách:
- Cách 1:
Bước 1: Với ∆x là số gia của đối số tại x0 ta tính ∆y = f(x0 + ∆x) − f(x0)
Bước 2: Tính giới hạn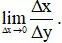 
- Cách 2: Đạo hàm của hàm số tại x0 là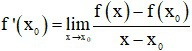 
e) Mối liên hệ giữa đạo hàm và tính liên tục
Định lí: Nếu hàm số f(x) có đạo hàm tại x0 thì f(x) liên tục tại x0.
Chú ý: Định lí trên chỉ là điều kiện cần, tức là một hàm có thể liên tục tại điểm x0 nhưng hàm đó không có đạo hàm tại x0.
2. Các dạng bài tập
Dạng 1: Tìm số gia của hàm số
Phương pháp giải:
Để tính số gia của hàm số y = f(x) tại điểm x0 tương ứng với số gia ∆x cho trước ta áp dụng công thức: ∆y = f(x0 + ∆x) − f(x0).
Ví dụ minh họa:
Ví dụ 1: Tìm số gia của hàm số y = f(x) = x3 – 3x2 + 2, biết rằng:
a) x0 = 1; ∆x = 1
b) x0 = 1; ∆x = −0,1
Lời giải
a) Số gia của hàm số là:
∆y = f(x0 + ∆x) − f(x0) = f(2) − f(1)
= 23 − 3.22 + 2 − (13 − 3.12 +2) = − 2
.b) Số gia của hàm số là:
∆y = f(x0 + ∆x) − f(x0) = f(0,9) − f(1)
= 0,93 − 3.0,92 +2 − (13 − 3.12 +2) = 0,299.
Ví dụ 2: Tìm số gia của hàm số:
a) y = 2x + 3
b) y = 2x2 – 3x + 1 tại x0 = 1
Lời giải
a) Số gia của hàm số là:
∆y = f(x0 + ∆x) − f(x0)
= 2(x0 + ∆x) + 3 − (2x0 + 3) = 2∆x
b) Số gia của hàm số là:
∆y = f(1 + ∆x) − f(1)
= 2(1 + ∆x)2 − 3(1 + ∆x) + 1 − (2.12 − 3.1 +1)
= 2 + 4∆x + 2(∆x)2 − 3 − 3∆x +1 − 0
= 2(∆x)2 + ∆x.
Dạng 2: Tính đạo hàm bằng định nghĩa
Phương pháp giải:
Muốn tính đạo hàm của hàm số tại điểm x0 theo định nghĩa, ta có 2 cách:
Cách 1:
Bước 1: Với ∆x là số gia của đối số tại x0 ta tính ∆y = f(x0 + ∆x) − f(x0)
Bước 2: Tính giới hạn 
Cách 2: Đạo hàm của hàm số tại x0 là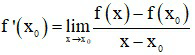 
Chú ý: Nếu không tồn tại giới hạn hữu hạn tại x0 thì hàm số không có đạo hàm tại x0.
Ví dụ minh họa:
Ví dụ 1: Tính đạo hàm (bằng định nghĩa) của các hàm số sau:
a) y = 2x2 + x + 1 tại x0 = 2.
b)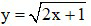 
tại x0 = 1.
c)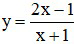 
tại x0 = 3
Lời giải
a) Cách 1: Với là số gia của đối số x0 = 2.
Khi đó hàm số số gia tương ứng:
∆y = f(x0 + ∆x) − f(x0)
= 2(2 + ∆x)2 + (2 + ∆x) + 1 − (2.22 − 2 +1)
= 8 + 8∆x + 2(∆x)2 + 2 + ∆x +1 − 11
= 9