Tổng hợp lý thuyết Phân số (hay, chi tiết)
Bài viết Tổng hợp lý thuyết Phân số lớp 6 hay, chi tiết giúp bạn nắm vững kiến thức trọng tâm về Phân số.
Tổng hợp lý thuyết Phân số (hay, chi tiết)
(199k) Xem Khóa học Toán 6 KNTTXem Khóa học Toán 6 CTSTXem Khóa học Toán 6 CD
A. Lý thuyết
1. Khái niệm phân số
Người ta gọi 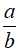
2. Hai phân số bằng nhau
Hai phân số a/b và c/d gọi là những phân số bằng nhau nếu a.d = b.c (tích chéo bằng nhau)
3. Tính chất cơ bản của phân số
+ Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho
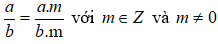
+ Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng ta được một phân số mới bằng phân số đã cho
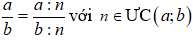
4. Cách rút gọn phân số
Muốn rút gọn phân số , ta chia cả tử và mẫu của phân số đó cho một ước chung khác 1 và -1 của chúng .
5. Phân số tối giản
+ Phân số tối giản (hay phân số không rút gọn được nữa ) là phân số mà cả tử và mẫu chỉ có ước chung là 1 và -1. Để rút gọn một lần mà được kết quả là phân số tối giản, chỉ cần chia tử và mẫu của phân số cho ƯCLN của chúng
+ Để rút gọn một phân số có thể phân tích tử và mẫu thành tích các thừa số
Chú ý:
+ Phân số a/b là tối giản nếu |a| và |b| là hai nguyên tố cùng nhau.
+ Khi rút gọn một phân số, người ta thường rút gọn về phân số tối giản.
6. Quy đồng mẫu hai phân số
Muốn quy đồng hai phân số ta làm như sau:
Bước 1: Tìm một bội chung của 2 mẫu số để làm mẫu chung
Bước 2: Tìm thừa số phụ của mỗi mẫu (chia mẫu chung cho từng mẫu)
Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng
7. Các bước quy đồng mẫu số nhiều phân số với mẫu số dương
Muốn quy đồng nhiều phân số với mẫu số dương ta làm như sau:
Bước 1: Tìm một bội chung của các mẫu (thường là BCNN) để là mẫu chung
Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng
8. So sánh hai phân số cùng mẫu
Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn
Ví dụ:
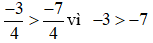
9. So sánh hai phân số không cùng mẫu
Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử với nhau: phân số nào có tử lớn hơn thì lớn hơn
Nhận xét:
+ Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn 0, gọi là phân số dương
+ Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn 0, gọi là phân số âm
Ta còn có cách so sánh phân số như sau:
• Áp dụng tính chất:
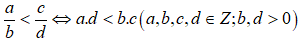
• Đưa về hai phân số cùng tử dương rồi so sánh mẫu (chỉ áp dụng đối với hai phân số cùng dương)
+ Chọn số thứ ba làm trung gian
10. Cộng hai phân số cùng mẫu
Muốn cộng hai phân số cùng mẫu ta cộng các tử và giữ nguyên mẫu
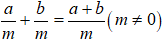
11. Cộng hai phân số khác mẫu
Muốn cộng hai phân số không cùng mẫu. ta viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử với nhau và giữ nguyên mẫu chung
12. Các tính chất
+ Tính chất giao hoán :
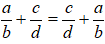
+ Tính chất kết hợp:
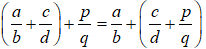
+ Cộng với số 0:
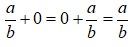
13. Số đối
Hai số gọi là đối nhau nêu tổng của chúng bằng
Kí hiệu số đối của phân số a/b và -a/b
Ví dụ: Số đối của 5/6 là -5/6
Số đối của -2/9 là 2/9.
14. Phép trừ phân số
Muốn trừ một phân số cho một phân số, ta cộng số bị trừ với số đối của số trừ
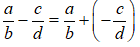
15. Quy tắc phép nhân phân số
+ Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau
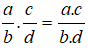
+ Muốn nhân một số nguyên với một phân số ( hoặc một phân số với một số nguyên ), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu
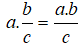
16. Các tính chất cơ bản của phân số
+ Tính chất giao hoán:
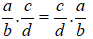
+ Tính chất kết hợp:
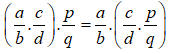
+ Nhân với số 1:
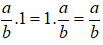
+ Nhân với số 0:
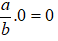
+ Tính chất phân phối của phép nhân đối với phép cộng:
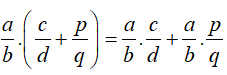
Nhận xét:
Lũy thừa của một phân số: Với n ∈ N thừa số
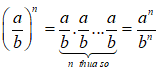
17. Số nghịch đảo
Hai số gọi là nghịch đảo của nhau nếu tích của chúng bằng 1
Ví dụ:
Số nghich đảo của 1/6 là 6; số nghịch đảo của -5 là -1/5.
18. Phép chia phân số
Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia
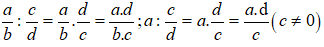
19. Hỗn số
+ Nếu phân số dương lớn hơn 1, ta có thể viết nó dưới dạng hỗn số bằng cách: chia tử cho mẫu, thương tìm được là nguyên của hỗn số, số dư là tử của phân số kèm theo, còn mẫu vẫn là mẫu đã cho
+ Muốn viết một hỗn số dưới dạng một phân số, ta nhân phần nguyên với mẫu rồi cộng với tử, kết quả tìm được là tử số của phân số, còn mẫu vẫn là mẫu đã cho
+ Khi viết một phân số âm dưới dạng hỗn số, ta chỉ cần viết số đối của nó dưới dạng hỗn số rồi đặt dấu “-“ trước kết quả nhận được
20. Số thập phân
Phân số thập phân là phân số mà mẫu là lũy thừa của 10
Các phân số thập phân có thể viết được dưới dạng số thập phân
+ Số thập phân gồm hai phần:
• Phần số nguyên viết bên trái dấu phẩy
• Phần thập phân viết bên phải dấu phẩy
Số chữ số của phần thập phân đúng bằng số chữ số 0 ở mẫu của phân số thập phân.
21. Phần trăm
Những phân số có mẫu là 100 còn được viết dưới dạng phần trăm với kí hiệu %
Ví dụ:
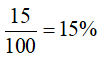
22. Tìm giá trị phân số của một số cho trước
Muốn tìm 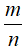
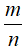
23. Tìm một số biết giá trị một phân số của nó
Muốn tìm một số biết 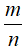
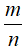
24. Tỉ số của hai số
Thương trong phép chia số a cho số b (b ≠ 0) gọi là tỉ số của a và b
Kí hiệu a:b hoặc a/b
Ví dụ:
Tỉ số của
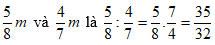
25. Tỉ số phần trăm
Muốn tìm tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào kết quả:
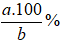
Ví dụ:
Tỉ số phần trăm của 2kg và 40kg là:
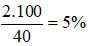
26. Tỉ lệ xích
Tỉ lệ xích T của một bản vẽ (hoặc một bản đồ) là tỉ số khoảng cách a giữa hai điểm trên bản vẽ ( hoặc bản đồ ) và khoảng cách b giữa hai điểm tương ứng thực tế: T = a/b ( có cùng đơn vị đo)
27. Biểu đồ phần trăm
Để nêu bật và so sánh một cách trực quan các giá trị phần trăm của cùng một đại lượng, người ta dùng biểu đồ phần trăm. Biểu đồ phần trăm thường được dựng dưới dạng cột, ô vuông và hình quạt
B. Bài tập
Câu 1: Trong các cách viết sau cách viết nào cho ta phân số: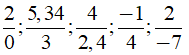
Lời giải:
Theo định nghĩa người ta gọi là phân số khi cả tử và mẫu đều là số nguyên và mẫu khác 0
⇒ -1/4; 2/-7 là phân số.
Câu 2: Viết các phép chia sau dưới dạng phân số
a) 5:13 b) -2:9 c) k:(-5) (k ∈ Z)
Lời giải:
a) Ta có: 5:13 ⇒ Có phân số là 5/13
b) Ta có: -2:9 ⇒ Có phân số là -2/9
c) Ta có: k:(-5) (k ∈ Z) ⇒ Có phân số là k/-5
Câu 3: Quy đồng mẫu các phân số sau: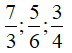
Lời giải:
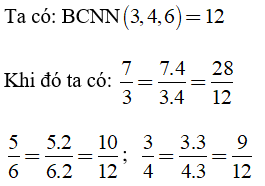
Câu 4: Rút gọn hai biểu thức rồi quy đồng
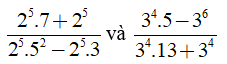
Lời giải:
Ta có:
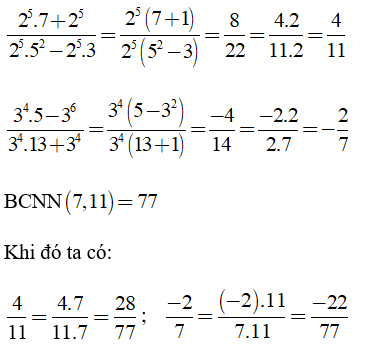
Câu 5: Tính
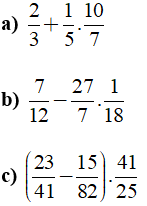
Lời giải:
a) Ta có:
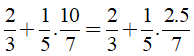
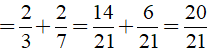
b) Ta có:
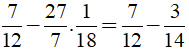
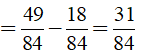
c) Ta có:
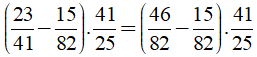
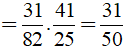
Câu 6: Cho phân số a/b và phân số a/c có b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0). Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a = 8, b = -3
Lời giải:
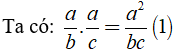
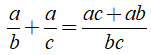
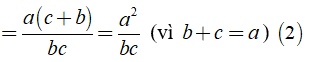
Từ (1), (2) ta có:
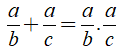
Nếu a = 8, b = -3 thì c = a - b = 8 - (-3) = 11
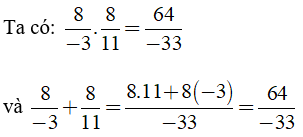
Câu 7: So sánh
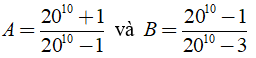
Lời giải:
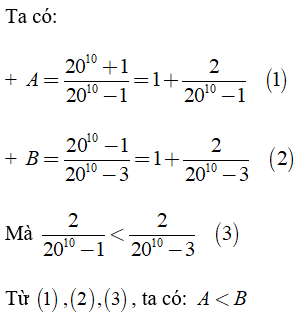
Câu 8: Tính
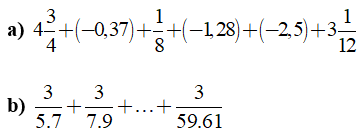
Lời giải:
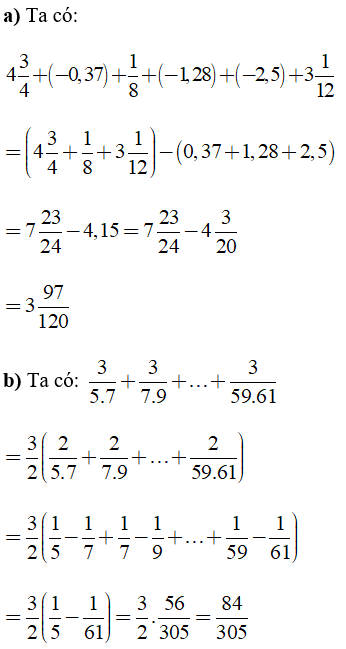
Câu 9: Tính giá trị các biểu thức sau:
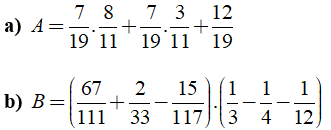
Lời giải:
a) Ta có:
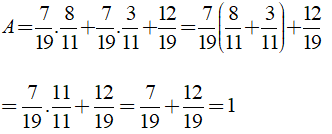
b) Ta có:
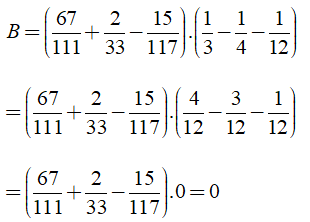
Câu 10: Lúc 6 giờ 50 phút Việt đi xe đạp từ A đến B với vận tốc 15km/h. Lúc 7 giờ 10 phút bạn Nam đi xe đạp từ B để đến A với vận tốc 12km/h. Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB.
Lời giải:
Thời gian bạn Việt đi quãng đường AC là:
7h30ph – 6h50ph = 40ph = 2/3 (h)
Quãng đường AC dài: 15.(2/3) = 10 (km)
Thời gian bạn Nam đi quãng đường BC là:
7h30ph – 7hl0ph = 20ph = 1/3 h.
Quãng đường BC dài: 12.(1/3) = 4 (km).
Độ dài quãng đường AB là: 10 + 4 = 14 (km).
Câu 11: Tính nhanh
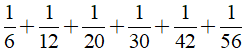
Lời giải:
Ta có:
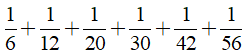
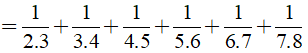
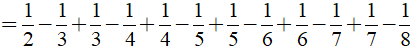
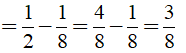
Câu 12: Chứng minh rằng
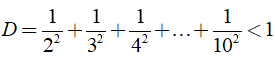
Lời giải:
Ta có:
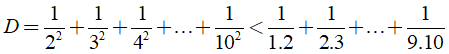
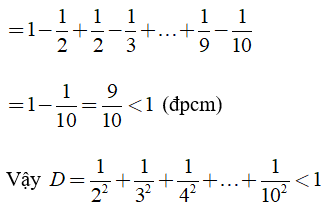
(199k) Xem Khóa học Toán 6 KNTTXem Khóa học Toán 6 CTSTXem Khóa học Toán 6 CD
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 6 có đáp án chi tiết hay khác:
- Lý thuyết Tìm tỉ số của hai số
- Bài tập Tìm tỉ số của hai số
- Lý thuyết Nửa mặt phẳng
- Bài tập Nửa mặt phẳng
- Lý thuyết Góc
Xem thêm các loạt bài Để học tốt Toán lớp 6 hay khác:
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Lý thuyết - Bài tập Toán lớp 6 có đầy đủ Lý thuyết và các dạng bài có lời giải chi tiết được biên soạn bám sát nội dung chương trình sgk Số học 6 và Hình học 6.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải sgk Tiếng Anh 6 Global Success
- Giải sgk Tiếng Anh 6 Friends plus
- Giải sgk Tiếng Anh 6 Smart World
- Giải sgk Tiếng Anh 6 Explore English
- Lớp 6 - Kết nối tri thức
- Soạn Văn 6 (hay nhất) - KNTT
- Soạn Văn 6 (ngắn nhất) - KNTT
- Giải sgk Toán 6 - KNTT
- Giải sgk Khoa học tự nhiên 6 - KNTT
- Giải sgk Lịch Sử 6 - KNTT
- Giải sgk Địa Lí 6 - KNTT
- Giải sgk Giáo dục công dân 6 - KNTT
- Giải sgk Hoạt động trải nghiệm 6 - KNTT
- Giải sgk Tin học 6 - KNTT
- Giải sgk Công nghệ 6 - KNTT
- Giải sgk Âm nhạc 6 - KNTT
- Lớp 6 - Chân trời sáng tạo
- Soạn Văn 6 (hay nhất) - CTST
- Soạn Văn 6 (ngắn nhất) - CTST
- Giải sgk Toán 6 - CTST
- Giải sgk Khoa học tự nhiên 6 - CTST
- Giải sgk Lịch Sử 6 - CTST
- Giải sgk Địa Lí 6 - CTST
- Giải sgk Giáo dục công dân 6 - CTST
- Giải sgk Công nghệ 6 - CTST
- Giải sgk Hoạt động trải nghiệm 6 - CTST
- Giải sgk Âm nhạc 6 - CTST
- Lớp 6 - Cánh diều
- Soạn Văn 6 Cánh diều (hay nhất)
- Soạn Văn 6 Cánh diều (ngắn nhất)
- Giải sgk Toán 6 - Cánh diều
- Giải sgk Khoa học tự nhiên 6 - Cánh diều
- Giải sgk Lịch Sử 6 - Cánh diều
- Giải sgk Địa Lí 6 - Cánh diều
- Giải sgk Giáo dục công dân 6 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 6 - Cánh diều
- Giải sgk Tin học 6 - Cánh diều
- Giải sgk Công nghệ 6 - Cánh diều
- Giải sgk Âm nhạc 6 - Cánh diều




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

