50 Bài tập Các trường hợp đồng dạng của tam giác lớp 8 (có đáp án)
Bài viết 50 Bài tập Các trường hợp đồng dạng của tam giác có đáp án gồm các dạng bài tập về Các trường hợp đồng dạng của tam giác lớp 8 gồm trường hợp đồng dạng thứ nhất, trường hợp đồng dạng thứ hai, trường hợp đồng dạng thứ ba từ cơ bản đến nâng cao giúp học sinh lớp 8 biết cách làm bài tập Các trường hợp đồng dạng của tam giác.
50 Bài tập Các trường hợp đồng dạng của tam giác lớp 8 (có đáp án)
(199k) Xem Khóa học Toán 8 KNTTXem Khóa học Toán 8 CTSTXem Khóa học Toán 8 CD
Bài tập Các trường hợp đồng dạng của tam giác (tổng hợp)
Bài 1: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Lời giải:
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta được
BC2 = AC2 + AB2 ⇒ AB = √ (BC2 - AC2) = √ (52 - 32) = 4( cm )
Ta có: cos ACBˆ = AC/BC = 3/5
Xét tam giác DEF có:
Khi đó ACBˆ = DEFˆ
Chọn đáp án B.
Bài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Lời giải:
Ta có: RS/PQ = RK/PM = SK/QM ⇒ Δ RSK ∼ Δ PQM
Chọn đáp án A.
Bài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Lời giải:
Ta có Δ RSK ∼ Δ PQM ⇔
Chọn đáp án A.
Bài 4: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Lời giải:
Ta có:
Chọn đáp án C.
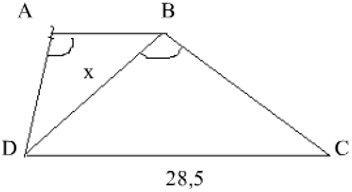
Bài 5: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
Lời giải:
Xét Δ ABD và Δ BDC có:
⇒ AB/BD = AD/BC = BD/DC
hay 12,5/x = x/28,5 ⇒ x2 = 1425/4 ⇔ x ≈ 18,87
Chọn đáp án D.
Bài 6: Cho tam giác ABC có M và N lần lượt là trung điểm của AC và AB. Gọi AD là tia phân giác của góc BACˆ = DBCˆ, tia AD cắt MN tại P. Hỏi tam giác nào đồng dạng với tam giác ANP
A. Δ ABD B. ΔAMP
C. ΔABD D. Δ ACD
Lời giải:
Xét tam giác ABC có M và N lần lượt là trung điểm của AC và AB nên MN là đường trung bình của tam giác ABC
Suy ra: MN // BC
Xét tam giác ABD có MP// BD (vì MN// BC)
Suy ra: Tam giác ANP đồng dạng với tam giác ABD.
Chọn đáp án A
Bài 7: Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, gọi F là giao điểm của DE và BC. Tìm khẳng định sai ?
A. Δ DAE đồng dạng Δ FBE
B. Δ DAE đồng dạng ΔFCD
C. Δ DEA đồng dạng ΔFCD
D. Δ FBE đồng dạng ΔFCD
Lời giải:
* Xét tam giác DAE và ΔFBE có:
∠AED = ∠BEF (2 góc đối đỉnh)
∠ADE = ∠EFB (2 góc so le trong )
Suy ra: Δ DAE đồng dạng Δ FBE ( g.g) (1)
* Vì ABCD là hình bình hành nên: BE// CD
Suy ra: Δ FBE đồng dạng ΔFCD ( định lí) (2)
Từ (1) và (2) suy ra Δ DAE đồng dạng ΔFCD ( bắc cầu)
Chọn đáp án C
Bài 8: Cho tam giác ABC có AB = 3cm, AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; NP = 10cm . Tìm khẳng định sai?
A. Tam giác ABC là tam giác nhọn
B. Δ ABC đồng dạng tam giác MNP
C. Tam giác ABC vuông tại A.
D. MP = 8cm
Lời giải:
* Ta có: AB2 + AC2 = BC2 (32 + 42 = 52 = 25 )
Suy ra: tam giác ABC vuông tại A.
* Áp dụng định lí Py ta go vào tam giác MNP ta có:
NP2 = MN2 + MP2
Suy ra: MP2 = NP2 – MN2 = 102 – 62 = 64
Do đó MP = 8cm.
*Ta có:
Do đó, Δ ABC đồng dạng tam giác MNP (c.c.c)
Chọn đáp án A
Bài 9: Cho tam giác ABC có M, N và P lần lượt là trung điểm của AB ; AC; BC. Tìm khẳng định sai
A. ΔAMN đồng dạng ΔABC ( định lí)
B. ΔCNP đồng dạng ΔCAB ( định lí)
C. ΔAMN đồng dạng ΔNPC
D. Chỉ có đúng 2 cặp tam giác đồng dạng .
Lời giải:
* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra : MN// BC
Tương tự có NP // AB
* Xét Δ AMN và ΔNPC có:
∠MAN = ∠PNC ( hai góc đồng vị )
∠ANM = ∠NCP ( hai góc đồng vị)
Suy ra: Δ AMN đồng dạng ΔNPC (g.g)
* Vì MN// BC nên ΔAMN đồng dạng ΔABC ( định lí)
* Vì NP // AB nên Δ CNP đồng dạng Δ CAB ( định lí)
Chọn đáp án D
Bài 10: Cho tam giác ABC có M là trung điểm của AC. Lấy điểm D đối xứng với B qua M . Khi đó :
A. Tứ giác ABCD là hình thoi
B. AC = BD
C. ΔAMB = ΔCMD theo tỉ số đồng dạng k = 1
D.
Lời giải:
Xét Δ AMB và ΔCMD có:
AM = MC ( vì M là trung điểm của AC)
∠AMB = ∠CMD = 90o
BM = MD ( vì D đối xứng với B qua M)
Suy ra: Δ AMB = ΔCMD ( c.g.c)
Suy ra: Hai tam giác này cũng đồng dạng với nhau và tỉ số đồng dạng là:
D.
Chọn đáp án C
Bài tập Trường hợp đồng dạng thứ nhất
Bài 11: Cho ΔABC đồng dạng với ΔMNP. Biết AB = 5cm, BC = 6cm, MN = 10cm, MP = 5cm. Hãy chọn câu đúng:
A. NP = 12cm, AC = 2,5cm
B. NP = 2,5cm, AC = 12cm
C. NP = 5cm, AC = 10cm
D. NP = 10cm, AC = 5cm
Lời giải
Đáp án cần chọn là: A
Bài 12: Cho ΔABC đồng dạng với ΔMNP. Biết AB = 2cm, BC = 3cm, MN = 6cm, MP = 6cm. Hãy chọn khẳng định sai:
A. AC = 2cm
B. NP = 9cm
C. ΔMNP cân tại M
D. ΔABC cân tại C
Lời giải
Vậy NP = 9cm, AC = 2cm nên A, B đúng.
Tam giác ABC cân tại A, MNP cân tại M nên C đúng, D sai.
Đáp án cần chọn là: D
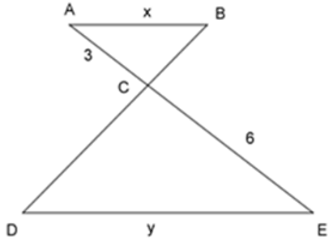
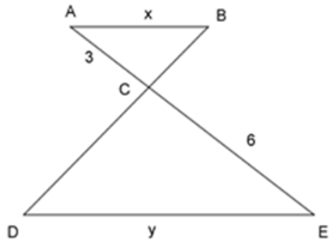
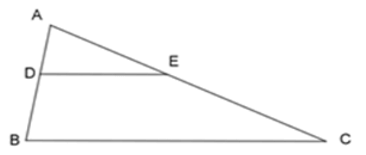
Bài 13: Cho tam giác ΔABC ~ ΔEDC như hình vẽ, tỉ số độ dài của x và y là:
Lời giải
Ta có: ΔABC ~ ΔEDC ⇒
Đáp án cần chọn là: B
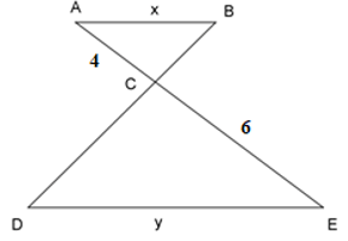
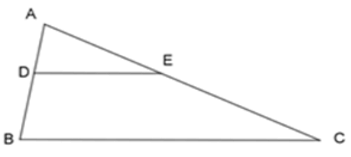
Bài 14: Cho tam giác ΔABC ~ ΔEDC như hình vẽ, tỉ số độ dài của x và y là:
Lời giải
Ta có: ΔABC ~ ΔEDC ⇒
Đáp án cần chọn là: B
Bài 15: ΔABC ~ ΔDEF theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2. ΔABC ~ ΔMNP theo tỉ số nào?
Lời giải
Vì ΔABC ~ ΔDEF theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2 nên ta có:
Đáp án cần chọn là: D
Bài 16: ΔDEF ~ ΔABC theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2. ΔABC ~ ΔMNP theo tỉ số nào?
Lời giải
Vì ΔDEF ~ ΔABC theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2 nên ta có:
Đáp án cần chọn là: A
Bài 17: Cho ΔABC ~ ΔIKH. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
A. 0
B. 1
C. 2
D. 3
Lời giải
Vì ΔABC ~ ΔIKH nên 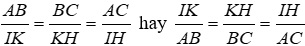
Đáp án cần chọn là: C
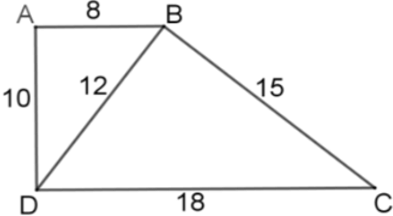
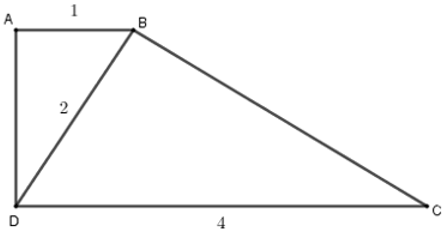
Bài 18: Tứ giác ABCD có AB = 8cm, BC = 15cm, CD = 18cm, AD = 10cm, BD = 12cm. Chọn câu đúng nhất:
A. ΔABD ~ ΔBDC
B. ABCD là hình thang
C. ABCD là hình thang vuông
D. Cả A, B đều đúng
Lời giải
Ta có:
Nên ΔABD ~ ΔBDC (c - c - c)
ΔABD ~ ΔBDC nên góc ABD = BDC.
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Lại có BD2 = 144 < 164 = AD2 + AB2 nên ΔABD không vuông. Do đó ABCD không là hình thang vuông
Vậy A, B đều đúng, C sai.
Đáp án cần chọn là: D
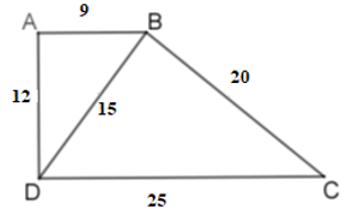
Bài 19: Tứ giác ABCD có AB = 9cm, BC = 20cm, CD = 25cm, AD = 12cm, BD = 15cm. Chọn câu sai:
A. ΔABD ~ ΔBDC
B. ABCD là hình thang
C. ABCD là hình thang vuông
D. ABCD là hình thang cân
Lời giải
Ta có:
Nên ΔABD ~ ΔBDC (c - c - c)
ΔABD ~ ΔBDC nên góc ABD = BDC.
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Lại có BD2 = 225 = AD2 + AB2 nên ΔABD vuông tại A. Do đó ABCD là hình thang vuông
Vậy A, B, C đều đúng, D sai
Đáp án cần chọn là: D
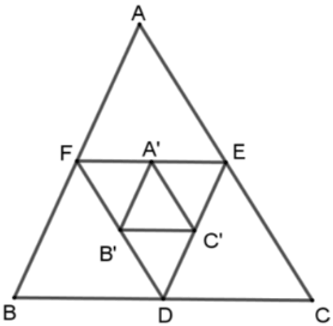
Bài 20: Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?
Lời giải
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên 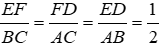
Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ ~ ΔDEF theo tỉ số k = 1/2
Đáp án cần chọn là: C
Bài tập Trường hợp đồng dạng thứ hai
Bài 21: Cho ΔABC, lấy 2 điểm D và E lần lượt nằm bên cạnh AB và AC sao cho 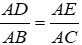
A. ΔADE ~ ΔABC
B. DE // BC
C. 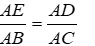
D. góc ADE = góc ABC
Lời giải
Đáp án cần chọn là: C
Bài 22: Cho ΔABC, trên cạnh AB lấy điểm D khác A, B. Qua D kẻ đường thẳng song song với BC cắt AC tại E. Chọn kết luận sai?
A. ΔADE ~ ΔABC
B. DE // BC
C. 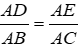
D. góc ADE = góc ACB
Lời giải
Do DE // BC nên theo định lý Talet đảo ta có 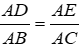
Xét ΔADE và ΔABC ta có:
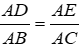
A chung.
⇒ ΔADE ~ ΔABC (c - g - c) nên A đúng
⇒ ADE = ABC (cặp góc tương ứng) nên D sai.
⇒
Đáp án cần chọn là: D
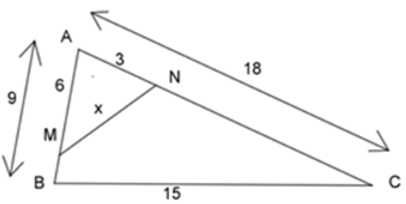
Bài 23: Cho hình vẽ dưới đây, tính giá trị của x?
A. x = 6
B. x = 5
C. x = 8
D. x = 9
Lời giải
Đáp án cần chọn là: B
Bài 24: Cho hình vẽ dưới đây, tính giá trị của x?
A. x = 4
B. x = 16
C. x = 10
D. x = 14
Lời giải
Đáp án cần chọn là: B
Bài 25: Với AB // CD thì giá trị của x trong hình vẽ dưới đây là
A. x = 15
B. x = 16
C. x = 7
D. x = 8
Lời giải
Đáp án cần chọn là: A
Bài 26: Cho hình thang ABCD có: AB // CD, AB = 4, CD = 16, AC = 8, AD = 12. Độ dài BC là:
A. 8
B. 13
C. 12
D. 6
Lời giải
Đáp án cần chọn là: D
Bài 27: Cho tam giác ABC có AB = 12cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho CD = 12cm. Tính độ dài AD.
A. 12cm
B. 6cm
C. 10cm
D. 8cm
Lời giải
Đáp án cần chọn là: D
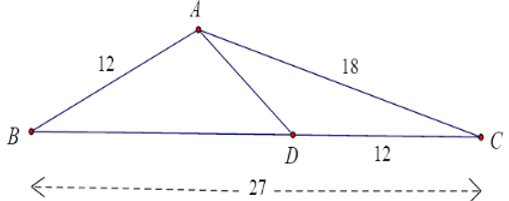
Bài 28: Cho tam giác ABC có AB = 15cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho 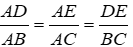
A. 12cm
B. 6cm
C. 10cm
D. 8cm
Lời giải
Đáp án cần chọn là: C
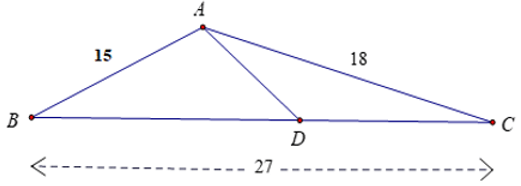
Bài 29: Cho hình thang vuông ABCD (A = D = 900) có AB = 16cm, CD = 25cm, BD = 20cm.
1. Tam giác ABD đồng dạng với tam giác nào dưới đây?
A. ΔBDC
B. ΔCBD
C. ΔBCD
D. ΔDCB
Lời giải
ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);
Và
Do đó ΔABD ~ ΔBDC (c.g.c)
Đáp án cần chọn là: A
2. Độ dài cạnh BC là
A. 10cm
B. 12cm
C. 15cm
D. 9cm
Lời giải
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 900 nên DBC = 900. Theo định lí Pytago, ta có
BC2 = CD2 - BD2 = 252 - 202 = 152. Vậy BC = 15cm
Đáp án cần chọn là: C
Bài 30: Cho hình thang vuông ABCD (A = D = 900) có AB = 1cm, CD = 4cm, BD = 2cm.
1.Chọn kết luận sai?
A. ΔABD ~ ΔBDC
B. BDC = 900
C. BC = 2AD
D. BD vuông góc BC
Lời giải
ΔABD và ΔBDC có: ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD)
Do đó ΔABD ~ ΔBDC (c.g.c) nên A đúng.
⇒ ABD = BDC < 900 nên B sai.
ΔABD ~ ΔBDC ⇒ 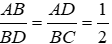
BAD = DBC = 900 nên BD ⊥ BC hay D đúng
Vậy chỉ có B sai.
Đáp án cần chọn là: B
2. Độ dài cạn BC là (làm tròn đến hai chữ số thập phân)
A. 3cm
B. 4cm
C. 4,36cm
D. 3,46cm
Lời giải
Tam giác BDC vuông tại B (theo câu trên), định lý Pitago ta có:
BD2 + BC2 = CD2 ⇔ 22 + BC2 = 42 ⇔ BC2 = 12 ⇒ BC ≈ 3,46
Đáp án cần chọn là: D
Bài tập Trường hợp đồng dạng thứ ba
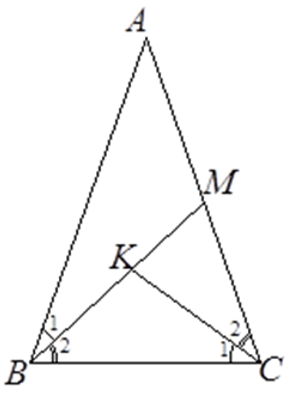
Bài 31: Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc BCK = góc ABM.
1. Tam giác MBC đồng dạng với tam giác
A. MCK
B. MKC
C. KMC
D. CMK
Lời giải
Tam giác ABC cân tại A nên góc ABC = góc ACB, ta lại có B1 = C1 (gt) nên B2 = C2.
ΔMBC và ΔMCK có:
BMC là góc chung;
B2 = C2 (cmt)
Do đó ΔMBC ~ ΔMCK (g.g).
Đáp án cần chọn là: A
2. Tính MB.MK bằng
A. 2MC2
B. CA2
C. MC2
D. BC2
Lời giải
Vì ΔMBC ~ ΔMCK nên 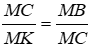
Suy ra MC2 = MB.MK
Đáp án cần chọn là: C
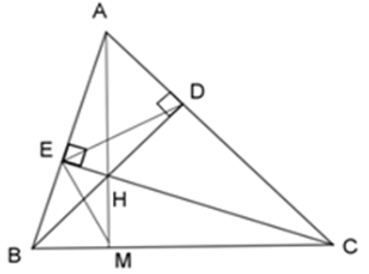
Bài 32: Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.
1. Chọn câu đúng.
A. ΔHBE ~ ΔHCD
B. ΔABD ~ ΔACE
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Xét ΔHBE và ΔHCD có:
góc BDC = góc CEB = 900
góc EHB = góc DHC (2 góc đối đỉnh)
⇒ ΔHBE ~ ΔHCD (g - g)
Xét ΔABD và ΔACE có
góc AEC = góc BDA = 900
Góc A chung
Nên ΔABD ~ ΔACE (g - g)
Đáp án cần chọn là: C
2. Chọn khẳng định sai.
A. góc HDE = góc HCB
B. góc AMB = 900
C. góc HDE = góc HAE
D. góc HDE = góc HAD
Lời giải
góc EHD = góc HAE (hai góc đối đỉnh)
góc HDE = góc HAE
⇒ ΔHED ~ ΔHBC (c - g - c)
⇒ góc HDE = góc HCB (1)
Mà đường cao BD và CE cắt nhau tại H (theo giả thiết)
⇒ H là trực tâm của ΔABC
⇒ AH ⊥ BC tại M ⇒ AMB = 900
Xét ΔAMB và ΔCEB có:
góc CEB = góc AMB = 900
B chung
⇒ ΔAMB ~ ΔCEB (g - g)
⇒ góc MAB = góc ECB hay góc HAE = góc HCB (2)
Từ (1) và (2) ta có: góc HDE = góc HAE nên A, B, C đúng, D sai.
Đáp án cần chọn là: D
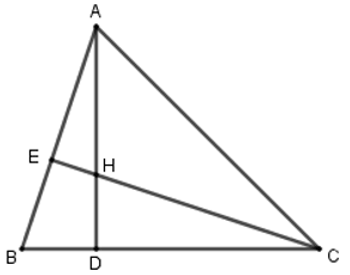
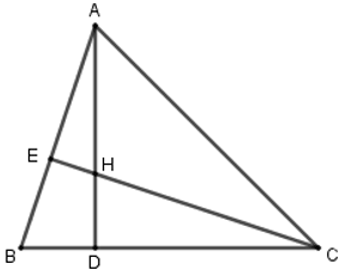
Bài 33: Cho ΔABC có đường cao AD, CE và trực tâm H.
1. Chọn câu trả lời đúng nhất.
A. ΔADB ~ ΔCDH
B. ΔABD ~ ΔCBE
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Xét tam giác ABD và CBE có:
E = D = 900
Chung B
⇒ ΔABD ~ ΔCBE (g - g)
⇒ góc BAD = góc BCE = góc DCH (góc t/ư)
Xét ΔADB và ΔCDH có:
góc ADB = góc CDH = 900
góc BAD = góc DCH (cmt)
⇒ ΔADB ~ ΔCDH (g - g)
Vậy A, B đều đúng
Đáp án cần chọn là: C
2. Chọn khẳng định sai.
Lời giải
Đáp án cần chọn là: C
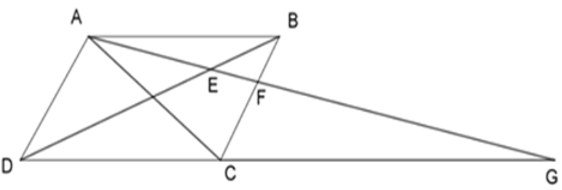
Bài 34: Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
A. ΔBFE ~ ΔDAE
B. ΔDEG ~ ΔBEA
C. ΔBFE ~ ΔDEA
D. ΔDGE ~ ΔBAE
Lời giải
Có ABCD là hình bình hành nên: AD // BC, AB // DC
⇒ góc ADE = góc FBE (cặp góc so le trong)
⇒ góc ABE = góc EDG (cặp góc so le trong)
Xét tam giác BFE và tam ggiacs DAE có:
góc ADE = góc FBE (cmt)
góc AED = góc FEB (đối đỉnh)
⇒ ΔBFE ~ ΔDAE (g - g) nên A đúng, C sai.
Xét tam giác DGE và tam giác BAE có:
góc ABE = góc EDG (cmt)
góc AEB = góc GED (đối đỉnh)
⇒ ΔDGE ~ ΔBAE (g - g) hay ΔDEG ~ ΔBEA nên B, D đúng
Đáp án cần chọn là: C
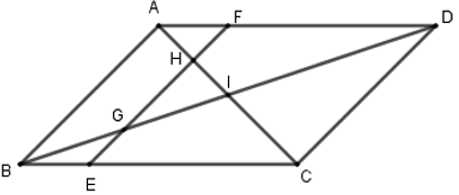
Bài 35: Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
A. ΔBGE ~ ΔHGI
B. ΔGHI ~ ΔBAI
C. ΔBGE ~ ΔDGF
D. ΔAHF ~ ΔCHE
Lời giải
Có ABCD là hình bình hành nên: AD // BC, AB // DC
Xét ΔBGE và ΔDGF có:
● góc BGE = góc DGF (đối đỉnh)
● góc EBG = góc FDG (so le trong)
⇒ ΔBGE ~ ΔDGF (g-g) nên C đúng
Xét ΔAHF và ΔCHE có:
● góc AHF = góc CHE (đối đỉnh)
● góc HAF = góc HCE (so le trong)
⇒ ΔAHF ~ ΔCHE (g-g) nên D đúng
Lại có GH // AB ⇒ IHG = IAB (đồng vị)
Xét ΔGHI và ΔBAI có
● Chung I
● góc IHG = góc IAB (cmt)
⇒ ΔGHI ~ ΔBAI (g-g)
Suy ra B đúng
Chỉ có A sai.
Đáp án cần chọn là: A
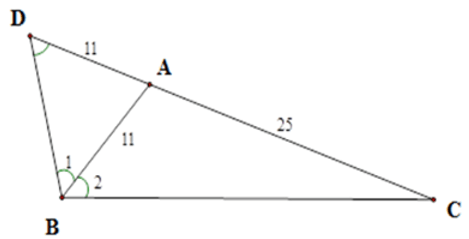
Bài 36: Tam giác ABC có A = 2B, AB = 11cm, AC = 25cm. Tính độ dài cạnh BC.
A. 30cm
B. 20cm
C. 25cm
D. 15cm
Lời giải
Trên tia đối của tia AC lấy điểm D sao cho AD = AB.
Tam giác ABD cân tại A nên góc BAC = B1 + D = 2D.
Ta lại có góc BAC = 2B2 nên D = B2.
Xét ΔCBA và ΔCDB có C chung và D = B2.
Nên ΔCBA ~ ΔCDB (g-g) nên
Từ đó BC2 = 25.36 suy ra BC = 5.6 = 30(cm)
Đáp án cần chọn là: A
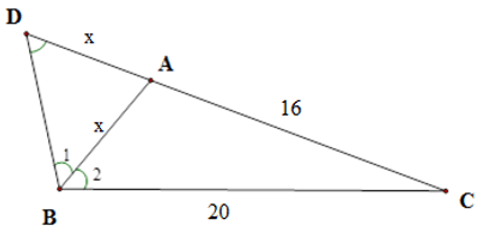
Bài 37: Tam giác ABC có A = 2B, AC = 16cm, BC = 20cm. Tính độ dài cạnh AB.
A. 18cm
B. 20cm
C. 15cm
D. 9cm
Lời giải
Trên tia đối của tia AC lấy điểm D sao cho AD = AB.
Tam giác ABD cân tại A nên góc BAC = B1 + D = 2D.
Ta lại có góc BAC = 2B2 nên D = B2.
Xét ΔCBA và ΔCDB có C chung và D = B2.
⇒ x = 25 - 16 = 9 (cm)
Vậy AB = 9cm
Đáp án cần chọn là: D
Bài 38: Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho góc DME = góc ABC.
1. Tính BD.CE bằng
A. 2a2
B. 3a
C. a2
D. 4a2
Lời giải
+ Ta có: góc DMC = góc DME + góc EMC
Mặt khác: góc DMC = góc ABC + góc BDM (góc ngoài tam giác)
Mà: góc DME = góc ABC (gt) nên BDM = EMC
+ Ta có: góc ABC = góc ACB (ΔABC cân tại A) và góc BDM = góc EMC (cmt)
⇒ ΔBDM ~ ΔCME (g - g)
⇒ 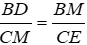
Lại có M là trung điểm của BC và BC = 2a ⇒ BM = MC = a
⇒ BD.CE = a2 không đổi
Đáp án cần chọn là: C
2. Góc BDM bằng với góc nào dưới đây?
A. DEM
B. MDE
C. ADE
D. AED
Lời giải
Đáp án cần chọn là: B
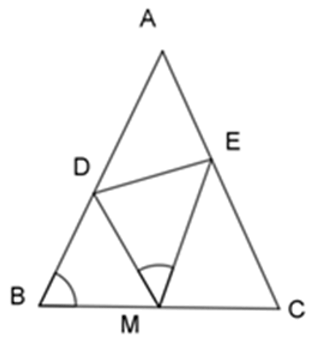
Bài 39: Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE.
1. Chọn khẳng định đúng.
A. góc ADE = góc AED
B. góc BDM = góc MEC
C. góc DEM = góc CEM
D. góc BMD = góc CME
Lời giải
Tam giác ABC có: M là trung điểm của BC nên AM vừa là đường trung tuyến vừa là đường phân giác trong góc A.
Lại có: DM là ghân giác của góc BDE nên DM là phân giác ngoài góc D của tam giác ADE.
Tam giác ADE có phân giác trong AM cắt phân giác ngoài DM tại M nên EM là đường phân giác ngoài góc E hay EM là phân giác của góc DEC.
Vậy góc DEM = góc CEM.
Đáp án cần chọn là: C
2. Chọn kết luận đúng.
A. ΔBDM ~ ΔCME
B. ΔBDM ~ ΔEMC
C. ΔBDM ~ ΔCEM
D. ΔBDM ~ ΔECM
Lời giải
Đặt B = C = x, góc BDM = góc EDM = y, góc CEM = góc DEM = z
Tứ giác BDCE có: B + C + BDE + CED = 3600
⇒ 2x + 2y + 2z = 3600 ⇔ x + y + z = 1800
Hay B + góc BDM + góc CEM = 1800
Mà B + góc BDM + góc BMD = 1800 (tổng ba góc trong tam giác)
Nên góc CEM = góc BMD
Xét ΔBDM và ΔCME có:
● B = C (gt)
● góc BMD = góc CEM (cmt)
⇒ ΔBDM ~ ΔCME (g - g)
Đáp án cần chọn là: A
Bài 40: Nếu 2 tam giác ABC và DEF có A = D, C = F thì:
A. ΔABC ~ ΔDEF
B. ΔCAB ~ ΔDEF
C. ΔABC ~ ΔDFE
D. ΔCBA ~ ΔDFE
Lời giải
Xét ΔABC và ΔDEF có:
● A = D (gt)
● C = F (gt)
⇒ ΔABC ~ ΔDEF (g - g)
Đáp án cần chọn là: A
(199k) Xem Khóa học Toán 8 KNTTXem Khóa học Toán 8 CTSTXem Khóa học Toán 8 CD
Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 8 có đáp án chi tiết hay khác:
- Lý thuyết Các trường hợp đồng dạng của tam giác
- Lý thuyết Trường hợp đồng dạng thứ nhất
- Lý thuyết Trường hợp đồng dạng thứ hai
- Lý thuyết Trường hợp đồng dạng thứ ba
- Lý thuyết Các trường hợp đồng dạng của tam giác vuông
- Bài tập Các trường hợp đồng dạng của tam giác vuông
- Tổng hợp Lý thuyết & Trắc nghiệm Chương 3 Hình học 8
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Lý thuyết & 700 Bài tập Toán lớp 8 có lời giải chi tiết có đầy đủ Lý thuyết và các dạng bài có lời giải chi tiết được biên soạn bám sát nội dung chương trình sgk Đại số 8 và Hình học 8.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 8 Global Success
- Giải sgk Tiếng Anh 8 Smart World
- Giải sgk Tiếng Anh 8 Friends plus
- Lớp 8 - Kết nối tri thức
- Soạn văn 8 (hay nhất) - KNTT
- Soạn văn 8 (ngắn nhất) KNTT
- Giải sgk Toán 8 - KNTT
- Giải sgk Khoa học tự nhiên 8 - KNTT
- Giải sgk Lịch Sử 8 - KNTT
- Giải sgk Địa Lí 8 - KNTT
- Giải sgk Giáo dục công dân 8 - KNTT
- Giải sgk Tin học 8 - KNTT
- Giải sgk Công nghệ 8 - KNTT
- Giải sgk Hoạt động trải nghiệm 8 - KNTT
- Giải sgk Âm nhạc 8 - KNTT
- Lớp 8 - Chân trời sáng tạo
- Soạn văn 8 (hay nhất) - CTST
- Soạn văn 8 (ngắn nhất) - CTST
- Giải sgk Toán 8 - CTST
- Giải sgk Khoa học tự nhiên 8 - CTST
- Giải sgk Lịch Sử 8 - CTST
- Giải sgk Địa Lí 8 - CTST
- Giải sgk Giáo dục công dân 8 - CTST
- Giải sgk Tin học 8 - CTST
- Giải sgk Công nghệ 8 - CTST
- Giải sgk Hoạt động trải nghiệm 8 - CTST
- Giải sgk Âm nhạc 8 - CTST
- Lớp 8 - Cánh diều
- Soạn văn 8 Cánh diều (hay nhất)
- Soạn văn 8 Cánh diều (ngắn nhất)
- Giải sgk Toán 8 - Cánh diều
- Giải sgk Khoa học tự nhiên 8 - Cánh diều
- Giải sgk Lịch Sử 8 - Cánh diều
- Giải sgk Địa Lí 8 - Cánh diều
- Giải sgk Giáo dục công dân 8 - Cánh diều
- Giải sgk Tin học 8 - Cánh diều
- Giải sgk Công nghệ 8 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 8 - Cánh diều
- Giải sgk Âm nhạc 8 - Cánh diều

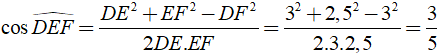

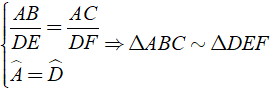
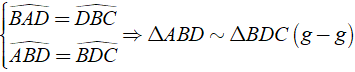
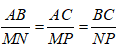
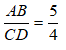
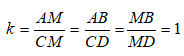
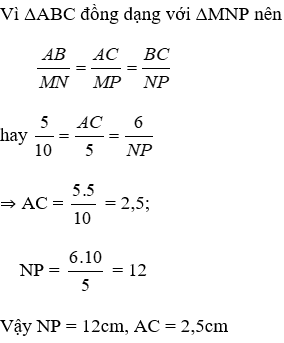

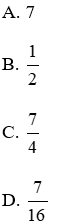
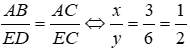
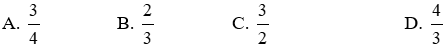
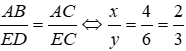
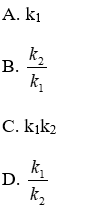
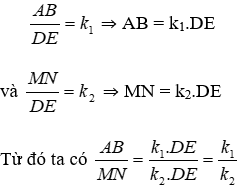
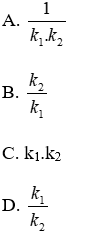
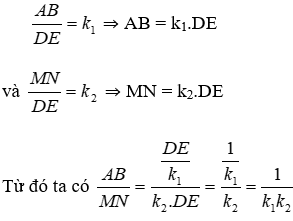
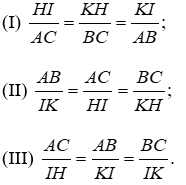
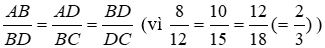
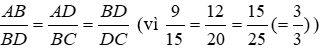
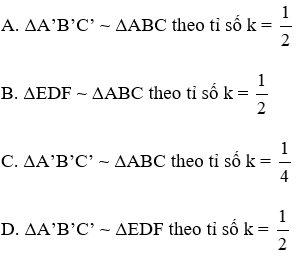




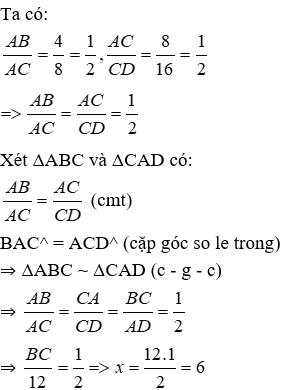


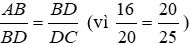
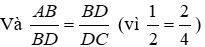
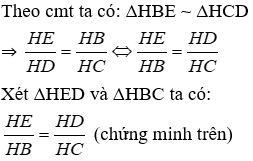
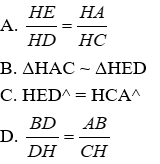
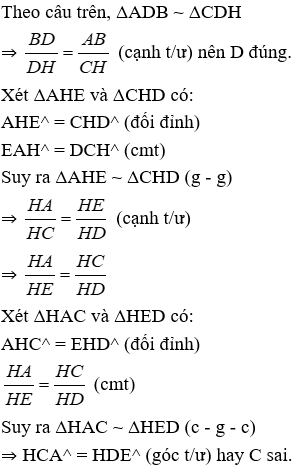

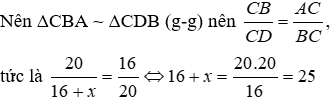




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

