20+ Bài tập trắc nghiệm Trường hợp đồng dạng thứ nhất lớp 8 (có đáp án)
Với bài tập trắc nghiệm Trường hợp đồng dạng thứ nhấtlớp 8 có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập trắc nghiệm Trường hợp đồng dạng thứ nhất
20+ Bài tập trắc nghiệm Trường hợp đồng dạng thứ nhất lớp 8 (có đáp án)
(199k) Học Toán 8 KNTTHọc Toán 8 CTSTHọc Toán 8 CD
Bài 1: Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
A. 4cm, 5cm, 6cm và 12cm, 15cm, 18cm.
B. 3cm, 4cm, 6cm và 9cm, 12cm, 18cm
C. 1,5cm, 2cm, 2cm và 1cm, 1cm, 1cm
D. 14cm, 15cm, 16cm và 7cm, 7,5cm, 8cm
Lời giải
Đáp án cần chọn là: C
Bài 2: Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
A. 2cm, 3cm, 4cm và 10cm, 15cm, 20cm.
B. 3cm, 4cm, 6cm và 9cm, 12cm, 16cm
C. 2cm, 2cm, 2cm và 1cm, 1cm, 1cm
D. 14cm, 15cm, 16cm và 7cm, 7,5cm, 8cm
Lời giải
Đáp án cần chọn là: B
Bài 3: Cho 2 tam giác RSK và PQM có 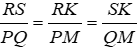
A. ΔRSK ~ ΔPQM
B. ΔRSK ~ ΔQPM
C. ΔRSK ~ ΔMPQ
D. ΔRSK ~ ΔQMP
Lời giải
2 tam giác RSK và PQM có 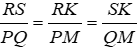
Đáp án cần chọn là: A
Bài 4: Cho 2 tam giác RSK và PQM có 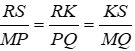
A. ΔRSK ~ ΔPQM
B. ΔRSK ~ ΔQPM
C. ΔRSK ~ ΔPMQ
D. ΔRSK ~ ΔQMP
Lời giải
2 tam giác RSK và PQM có 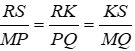
Đáp án cần chọn là: C
Bài 5: Cho ΔABC đồng dạng với ΔMNP. Biết AB = 5cm, BC = 6cm, MN = 10cm, MP = 5cm. Hãy chọn câu đúng:
A. NP = 12cm, AC = 2,5cm
B. NP = 2,5cm, AC = 12cm
C. NP = 5cm, AC = 10cm
D. NP = 10cm, AC = 5cm
Lời giải
Đáp án cần chọn là: A
Bài 6: Cho ΔABC đồng dạng với ΔMNP. Biết AB = 2cm, BC = 3cm, MN = 6cm, MP = 6cm. Hãy chọn khẳng định sai:
A. AC = 2cm
B. NP = 9cm
C. ΔMNP cân tại M
D. ΔABC cân tại C
Lời giải
Vậy NP = 9cm, AC = 2cm nên A, B đúng.
Tam giác ABC cân tại A, MNP cân tại M nên C đúng, D sai.
Đáp án cần chọn là: D
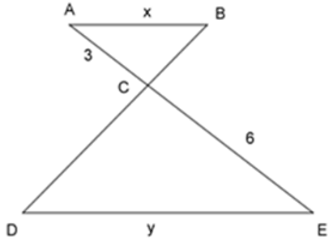
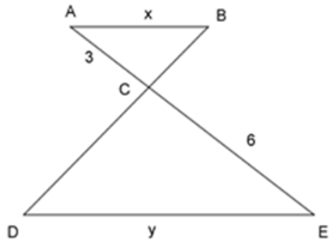
Bài 7: Cho tam giác ΔABC ~ ΔEDC như hình vẽ, tỉ số độ dài của x và y là:
Lời giải
Ta có: ΔABC ~ ΔEDC ⇒
Đáp án cần chọn là: B
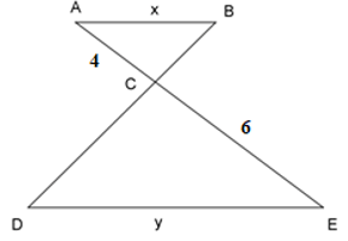
Bài 8: Cho tam giác ΔABC ~ ΔEDC như hình vẽ, tỉ số độ dài của x và y là:
Lời giải
Ta có: ΔABC ~ ΔEDC ⇒
Đáp án cần chọn là: B
Bài 9: ΔABC ~ ΔDEF theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2. ΔABC ~ ΔMNP theo tỉ số nào?
Lời giải
Vì ΔABC ~ ΔDEF theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2 nên ta có:
Đáp án cần chọn là: D
Bài 10: ΔDEF ~ ΔABC theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2. ΔABC ~ ΔMNP theo tỉ số nào?
Lời giải
Vì ΔDEF ~ ΔABC theo tỉ số k1, ΔMNP ~ ΔDEF theo tỉ số k2 nên ta có:
Đáp án cần chọn là: A
Bài 11: Cho ΔABC ~ ΔIKH. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
A. 0
B. 1
C. 2
D. 3
Lời giải
Vì ΔABC ~ ΔIKH nên 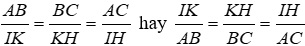
Đáp án cần chọn là: C
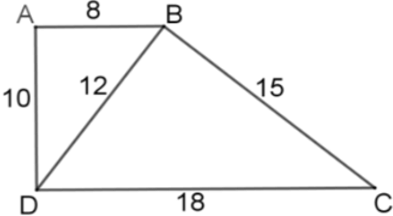
Bài 12: Tứ giác ABCD có AB = 8cm, BC = 15cm, CD = 18cm, AD = 10cm, BD = 12cm. Chọn câu đúng nhất:
A. ΔABD ~ ΔBDC
B. ABCD là hình thang
C. ABCD là hình thang vuông
D. Cả A, B đều đúng
Lời giải
Ta có:
Nên ΔABD ~ ΔBDC (c - c - c)
ΔABD ~ ΔBDC nên góc ABD = BDC.
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Lại có BD2 = 144 < 164 = AD2 + AB2 nên ΔABD không vuông. Do đó ABCD không là hình thang vuông
Vậy A, B đều đúng, C sai.
Đáp án cần chọn là: D
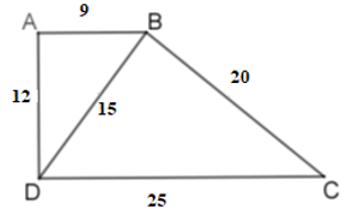
Bài 13: Tứ giác ABCD có AB = 9cm, BC = 20cm, CD = 25cm, AD = 12cm, BD = 15cm. Chọn câu sai:
A. ΔABD ~ ΔBDC
B. ABCD là hình thang
C. ABCD là hình thang vuông
D. ABCD là hình thang cân
Lời giải
Ta có:
Nên ΔABD ~ ΔBDC (c - c - c)
ΔABD ~ ΔBDC nên góc ABD = BDC.
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Lại có BD2 = 225 = AD2 + AB2 nên ΔABD vuông tại A. Do đó ABCD là hình thang vuông
Vậy A, B, C đều đúng, D sai
Đáp án cần chọn là: D
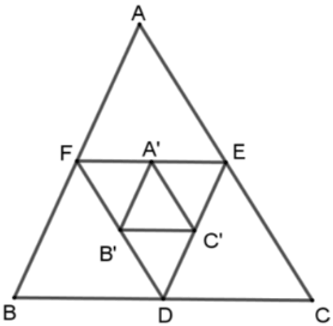
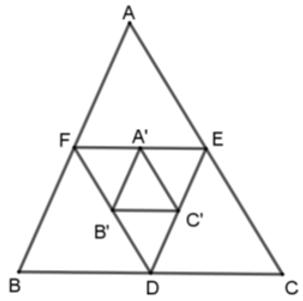
Bài 14: Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?
Lời giải
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên 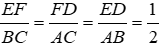
Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ ~ ΔDEF theo tỉ số k = 1/2
Đáp án cần chọn là: C
Bài 15: Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Xét các khẳng định sau:
Số khẳng định đúng là:
A. 2
B. 1
C. 3
D. 0
Lời giải
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên 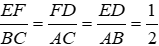

Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ ~ ΔDEF theo tỉ số k = 
Do đó ΔA’B’C’ ~ ΔABC (c - c - c) theo tỉ số k = 1/4 hay (II) đúng.
Do đó có 2 khẳng định đúng
Đáp án cần chọn là: A
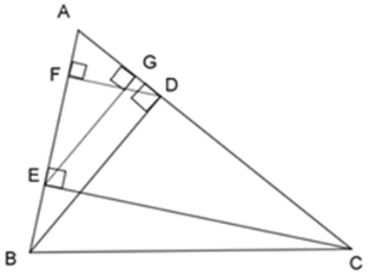
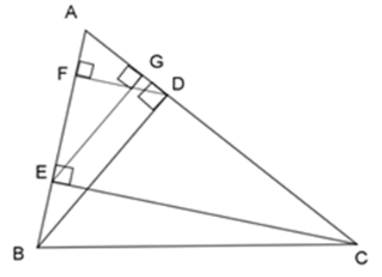
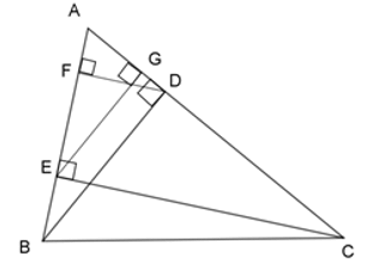
Bài 16: Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.
1. ΔABD đồng dạng với tam giác nào dưới đây?
A. ΔAEG
B. ΔABC
C. Cả A và B
D. Không có tam giác nào
Lời giải
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
⇒ BD // EG
Theo định lý Talet, ta có:
⇒ ΔAEG ~ ΔABD (c - c - c) (đpcm)
Đáp án cần chọn là: A
2. Chọn khẳng định đúng?
A. AD.AE = AB.AF
B. AD.AE = AB.AG = AC.AF
C. AD.AE = AC.GA
D. AD.AE = AB.AF = AC.AG
Lời giải
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án cần chọn là: B
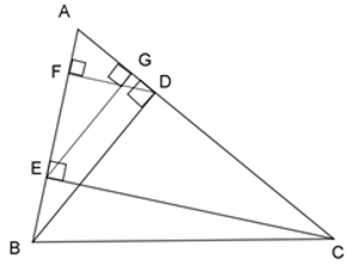
Bài 17: Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE.
1. Xét các cặp tam giác sau đây, số cặp tam giác đồng dạng với nhau là:
(1) ΔAEG và ΔABD
(2) ΔADF và ΔACE
(3) ΔABC và ΔAEC
A. 1
B. 0
C. 2
D. 3
Lời giải
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
⇒ BD // EG
Theo định lý Talet, ta có:
⇒ ΔAEG ~ ΔABD (c - c - c) nên (1) đúng.
Tương tự ta cũng chứng minh được ΔADF ~ ΔACE nên (2) đúng
Dễ thấy (3) sai vì
Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.
Đáp án cần chọn là: C
2. Chọn khẳng định không đúng?
A. AD.AE = AB.AFG
B. AD.AE = AC.AF
C. AD.AE = AC.FD
D. AE.EG = AB.BD
Lời giải
Đáp án cần chọn là: D
Bài 18: Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.
A. x = 5; y = 10
B. x = 6; y = 12
C. x = 12; y = 18
D. x = 6; y = 18
Lời giải
Tam giác thứ nhất có các cạnh là 8 < x < y
Tam giác thứ hai có các cạnh là x < y < 27
Vì hai tam giác đồng dạng nên 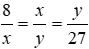
Do đó x2 = 8y = 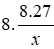
Vậy x = 12, y = 18
Đáp án cần chọn là: C
Bài 19: Một tam giác có cạnh nhỏ nhất bằng 12, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 40,5, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng, từ đó suy ra giá trị của S = x + y bằng:
A. 45
B. 60
C. 55
D. 35
Lời giải
Tam giác thứ nhất có các cạnh là 12 < x < y
Tam giác thứ hai có các cạnh là x < y < 40,5
Vì hai tam giác đồng dạng nên 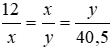
Do đó x2 = 12y = 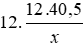
Suy ra y = 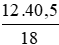
Vậy x = 18, y = 27 ⇒ S = 18 + 27 = 45
Đáp án cần chọn là: A
(199k) Học Toán 8 KNTTHọc Toán 8 CTSTHọc Toán 8 CD
Xem thêm các bài tập trắc nghiệm Toán lớp 8 có đáp án chi tiết hay khác:
- Trắc nghiệm Trường hợp đồng dạng thứ hai
- Trắc nghiệm Trường hợp đồng dạng thứ ba
- Trắc nghiệm Các trường hợp đồng dạng của tam giác vuông
- Top 21 Bài tập Tam giác đồng dạng (có lời giải)
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Lý thuyết & 700 Bài tập Toán lớp 8 có lời giải chi tiết có đầy đủ Lý thuyết và các dạng bài có lời giải chi tiết được biên soạn bám sát nội dung chương trình sgk Đại số 8 và Hình học 8.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 8 Global Success
- Giải sgk Tiếng Anh 8 Smart World
- Giải sgk Tiếng Anh 8 Friends plus
- Lớp 8 - Kết nối tri thức
- Soạn văn 8 (hay nhất) - KNTT
- Soạn văn 8 (ngắn nhất) KNTT
- Giải sgk Toán 8 - KNTT
- Giải sgk Khoa học tự nhiên 8 - KNTT
- Giải sgk Lịch Sử 8 - KNTT
- Giải sgk Địa Lí 8 - KNTT
- Giải sgk Giáo dục công dân 8 - KNTT
- Giải sgk Tin học 8 - KNTT
- Giải sgk Công nghệ 8 - KNTT
- Giải sgk Hoạt động trải nghiệm 8 - KNTT
- Giải sgk Âm nhạc 8 - KNTT
- Lớp 8 - Chân trời sáng tạo
- Soạn văn 8 (hay nhất) - CTST
- Soạn văn 8 (ngắn nhất) - CTST
- Giải sgk Toán 8 - CTST
- Giải sgk Khoa học tự nhiên 8 - CTST
- Giải sgk Lịch Sử 8 - CTST
- Giải sgk Địa Lí 8 - CTST
- Giải sgk Giáo dục công dân 8 - CTST
- Giải sgk Tin học 8 - CTST
- Giải sgk Công nghệ 8 - CTST
- Giải sgk Hoạt động trải nghiệm 8 - CTST
- Giải sgk Âm nhạc 8 - CTST
- Lớp 8 - Cánh diều
- Soạn văn 8 Cánh diều (hay nhất)
- Soạn văn 8 Cánh diều (ngắn nhất)
- Giải sgk Toán 8 - Cánh diều
- Giải sgk Khoa học tự nhiên 8 - Cánh diều
- Giải sgk Lịch Sử 8 - Cánh diều
- Giải sgk Địa Lí 8 - Cánh diều
- Giải sgk Giáo dục công dân 8 - Cánh diều
- Giải sgk Tin học 8 - Cánh diều
- Giải sgk Công nghệ 8 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 8 - Cánh diều
- Giải sgk Âm nhạc 8 - Cánh diều

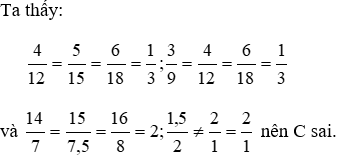

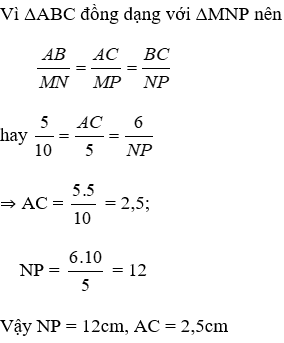

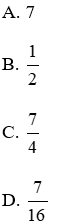
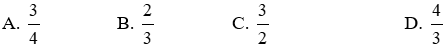
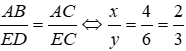
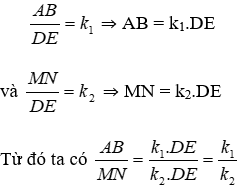
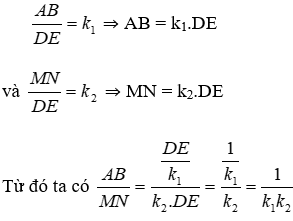
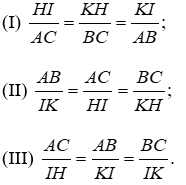
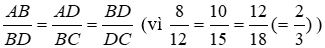
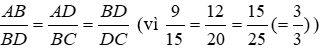


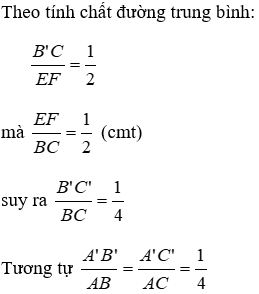
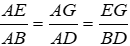

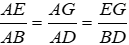
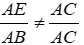
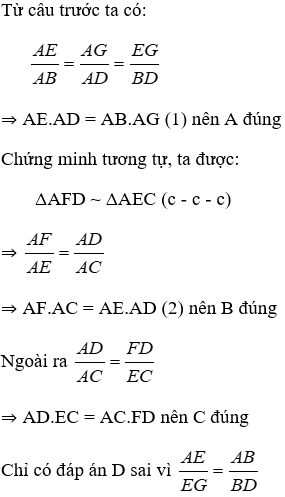



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

