Tổng hợp công thức Toán lớp 6 Học kì 2 (sách mới)
Bài viết tổng hợp công thức Toán lớp 6 Học kì 2 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều đầy đủ, chi tiết như là cuốn sổ tay công thức Toán lớp 6 giúp bạn học tốt môn Toán 6 hơn.
Tổng hợp công thức Toán lớp 6 Học kì 2 (sách mới)
Tổng hợp kiến thức, công thức Toán lớp 6 Chương 3 Số học
1. Khái niệm phân số: người ta gọi 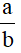
- Số nguyên a được coi là phân số với mẫu số là 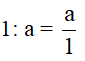
2. Hai phân số bằng nhau: Hai phân số 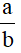
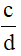
3. Tính chất cơ bản của phân số:
Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
4. Rút gọn phân số:
- Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.
- Phân số tối giản (hay phân số không rút gọn được nữa) là phân số mà cả tử và mẫu chỉ có ước chung là 1 và -1. Để rút gọn một lần mà được kết quả là phân số tối giản, chỉ cần chia tử và mẫu của phân số cho ƯCLN của chúng.
- Để rút gọn một phân số có thể phân tích tử và mẫu thành tích các thừa số.
5. Các bước quy đồng mẫu số nhiều phân số với mẫu số dương:
- Bước 1: Tìm một bội chung của các mẫu (thường là BCNN) để làm mẫu chung.
- Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).
- Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
6. So sánh hai phân số:
- Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
- Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử với nhau: phân số nào có tử lớn hơn thì lớn hơn.
- Nhận xét:
+ Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn 0, gọi là phân số dương.
+ Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn 0, gọi là phân số âm.
- Ta còn có các cách so sánh phân số như sau:
+ Áp dụng tính chất: 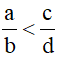
+ Đưa về hai phân số cùng tử rồi so sánh mẫu. VD: 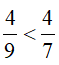
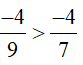
+ Chọn số thứ ba làm trung gian. VD: 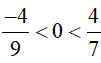
7. Các phép tính cộng, trừ, nhân, chia phân số:
8. Hỗn số, số thập phân, phần trăm:
- Một phân số lớn hơn 1 có thể viết dưới dạng hỗn số. Hỗn số có thể viết dưới dạng phân số.
+ Khi viết một phân số âm dưới dạng hỗn số, ta chỉ cần viết số đối của nó dưới dạng hỗn số rồi đặt dấu "-" trước kết quả nhận được.
- Phân số thập phân là phân số mà mẫu là lũy thừa của 10.
- Các phân số thập phân có thể viết được dưới dạng số thập phân.
Số thập phân gồm hai phần:
+ Phần số nguyên viết bên trái dấu phẩy.
+ Phần thập phân viết bên phải dấu phẩy.
Số chữ số của phần thập phân đúng bằng số chữ số 0 ở mẫu của phân số thập phân.
- Những phân số có mẫu số là 100 còn được viết dưới dạng phần trăm với kí hiệu %.
9. Ba bài toán cơ bản về phân số:
- Bài toán 1: Tìm giá trị phân số của một số cho trước:
Muốn tìm 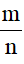
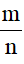
- Bài toán 2: Tìm một số biết giá trị một phân số của nó:
Muốn tìm một số biết 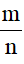
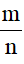
- Bài toán 3: Tìm tỉ số của hai số:
Tỉ số của hai số a và b là thương trong phép chia số a cho số b (b ≠ 0)
+ Tỉ số của a và b kí hiệu là a : b hoặc 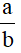
+ Khái niệm tỉ số thường được dùng khi nói về thương của hai đại lượng (cùng loại và cùng đơn vị đo)
+ Tỉ số không có đơn vị
* Tỉ số phần trăm: Muốn tìm tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào kết quả: 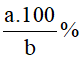
* Tỉ lệ xích: Tỉ lệ xích T của một bản vẽ (hoặc một bản đồ) là tỉ số khoảng cách a giữa hai điểm trên bản vẽ (hoặc bản đồ) và khoảng cách b giữa hai điểm tương ứng trên thực tế.
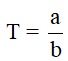
* Khi giải các bài toán cơ bản về phân số, ở một số bài toán đôi khi ta còn dùng phương pháp tính ngược từ cuối.
Tổng hợp kiến thức, công thức Toán lớp 6 Chương 2 Hình học
I. Nửa mặt phẳng:
a, Mặt phẳng:
- Một mặt bàn, mặt bảng, một tờ giấy trải rộng... cho ta hình ảnh của mặt phẳng.
- Mặt phẳng không bị hạn chế về mọi phía.
b, Nửa mặt phẳng:
- Hình gồm đường thẳng a và một phần mặt phẳng bị chia ra bởi a được gọi là một nửa mặt phẳng bờ a.
- Hai nửa mặt phẳng có chung bờ gọi là hai nửa mặt phẳng đối nhau.
- Bất kì đường thẳng nào nằm trên mặt phẳng cũng là bờ chung của hai nửa mặt phẳng đối nhau.
II. Góc:
1. Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia là đỉnh của góc. Hai tia là hai cạnh của góc ( 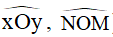
2. Điểm nằm bên trong góc: Khi hai tia Ox, Oy không đối nhau, điểm M là điểm nằm bên trong góc 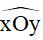
3. Góc bẹt là góc có hai cạnh là hai tia đối nhau 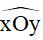
4. Góc có số đo bằng 900 là góc vuông (hay 1v).
Góc nhỏ hơn góc vuông là góc nhọn.
Góc lớn hơn góc vuông nhưng nhỏ hơn góc bẹt là góc tù.
Góc vuông:
Góc nhọn: 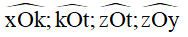
Góc tù: 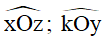
5. Cộng góc: Nếu tia Oy nằm giữa hai tia Ox và Oy thì 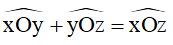
Ngược lại, nếu 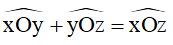
6. Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung.
7. Hai góc phụ nhau là hai góc có tổng số đo bằng 900
8. Hai góc bù nhau là hai góc có tổng số đo bằng 1800
9. Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù. (có tổng bằng 1800)
- Chú ý:
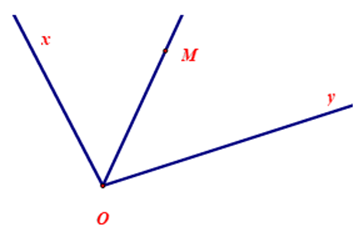
+ Với bất kì số m nào, , trên nửa mặt phẳng có bờ là đường thẳng chứa tia Ox bao giờ cũng vẽ được một và chỉ một tia Oy sao cho 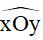
+ Nếu có các tia Oy, Oz thuộc cùng một nửa mặt phẳng bờ chứa tia Ox và 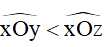
+ 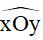
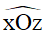
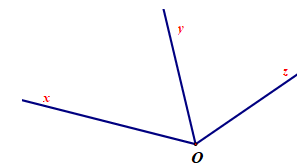
III. Tia phân giác của góc:
- Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
Tia Ot là tia phân giác của 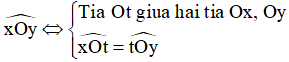
Hoặc: Tia Ot là tia phân giác của 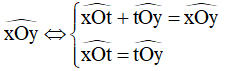
Hoặc: Tia Ot là tia phân giác của 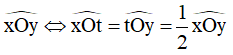
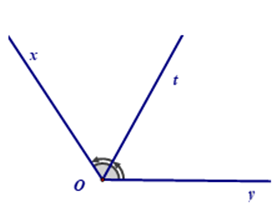
IV. Đường tròn:
- Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu (O;R).
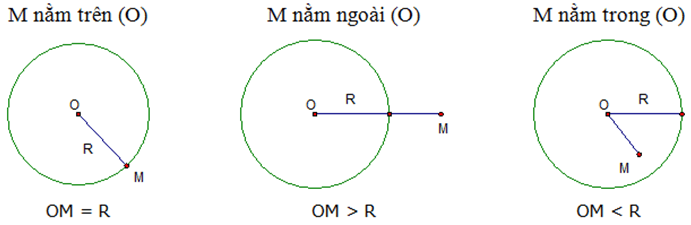
- Với mọi điểm M nằm trong mặt phẳng thì:
+ Nếu OM < R: điểm M nằm trong đường tròn
+ Nếu OM = R: điểm M nằm trên (thuộc) đường tròn.
+ Nếu OM > R: điểm M nằm ngoài đường tròn.
- Hình tròn: là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó.
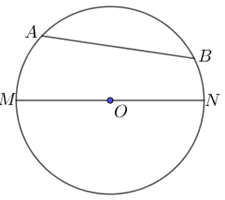
- Cung, dây cung, đường kính:
+ Hai điểm A, B nằm trên đường tròn chia đường tròn thành hai phần, mỗi phần gọi là một cung tròn (cung). Hai điểm A, B là hai mút của cung.
+ Đoạn thẳng AB gọi là một dây cung.
+ Dây cung đi qua tâm là đường kính (đường kính MN).
- Đường kính dài gấp đôi bán kính và là dây cung lớn nhất.
V. Tam giác:
- Tam giác ABC là hình gồm ba đoạn thẳng AB, BC, CA khi ba điểm A, B, C không thẳng hàng. Kí hiệu: ΔABC.
- Một tam giác có: 3 cạnh, 3 đỉnh, 3 góc.
- Một điểm nằm bên trong tam giác nếu nó nằm trong cả 3 góc của tam giác. Một điểm không nằm trong tam giác và không nằm trên cạnh nào của tam giác gọi là điểm ngoài của tam giác.
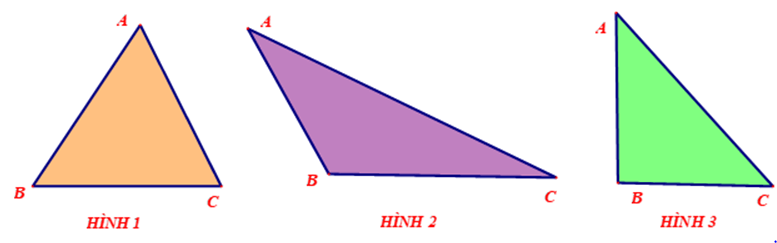
Tam giác có cả ba góc nhọn gọi là tam giác nhọn (HÌNH 1), có 1 góc tù là tam giác tù (HÌNH 2), có 1 góc vuông là tam giác vuông (HÌNH 3).
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài 500 Công thức, Định Lí, Định nghĩa Toán, Vật Lí, Hóa học, Sinh học được biên soạn bám sát nội dung chương trình học các cấp.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

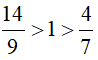

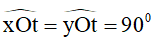






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

