Sách bài tập Toán 9 Bài 10: Diện tích hình tròn, hình quạt tròn
Sách bài tập Toán 9 Bài 10: Diện tích hình tròn, hình quạt tròn
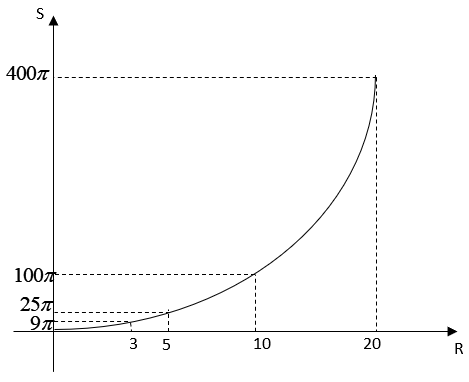
Bài 63 trang 111 Sách bài tập Toán 9 Tập 2: a.Điền vào ô trống trong bảng sau (S là diện tích hình tròn có bán kính R)
| R | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
| S |
b. Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó
c. Diện tích hình tròn có tỉ lệ thuận với bán kính không ?
Lời giải:
a.
| R | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
| S | 0 | π | 4π | 9π | 16π | 25π | 100π | 400π |
b.
c.Diện tích hình tròn không tỉ lệ thuận với bán kính
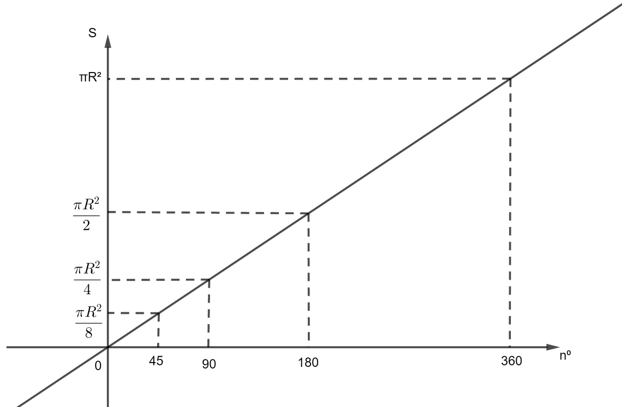
Bài 64 trang 111 Sách bài tập Toán 9 Tập 2: Điền vào ô trống trong bảng sau (S là diện tích hình quạt no)
| Cung no | 0 | 45 | 90 | 180 | 360 |
| S |
b. Vẽ đồ thị diện tích hình quạt theo no
c. Diện tích hình quạt có tỉ lệ thuận với số đo độ của cung không ?
Lời giải:
a.
| Cung no | 0 | 45 | 90 | 180 | 360 |
| S | 0 | (πR2)/8 | (πR2)/4 | (πR2)/2 | πR2 |
b.
Diện tích hình quạt tỉ lệ thuận với số đo độ của cung
Bài 65 trang 112 Sách bài tập Toán 9 Tập 2: Tính diện tích hình tròn biết chu vi của nó là C
Lời giải:
Gọi R và S lần lượt là bán kính và diện tích của hình tròn
Ta có:
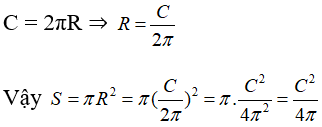
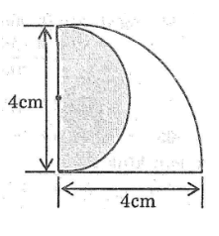
Bài 66 trang 112 Sách bài tập Toán 9 Tập 2: So sánh diện tích phần tô màu và phần để trắng trong hình sau:
Lời giải:
Phần tô màu là nửa hình tròn có đường kính 4cm nên bán kính bằng 2cm
Diện tích phần tô màu :
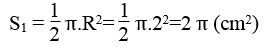
Diện tích cả hai hình là 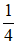
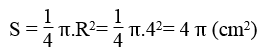
Diện tích phần để trắng : S2 = S - S1 = 4 π - 2 π =2 π (cm2)
vậy diện tích hai phần bằng nhau
Bài 67 trang 112 Sách bài tập Toán 9 Tập 2: a. Vẽ đường xoắn (hình sau) xuất phát từ một hình vuông cạnh 1cm.Nêu cách vẽ
b.Tính diện tích phần tô màu
Lời giải:
a. Cách vẽ:
-Vẽ 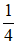
- Vẽ 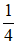
- Vẽ 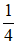
- Vẽ 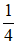
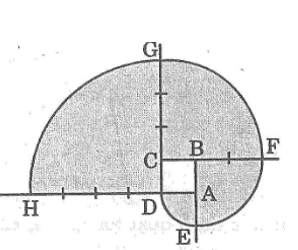
b.Ta có:
Bài 68 trang 112 Sách bài tập Toán 9 Tập 2: Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính 1,2 m. Người ta muốn nới rộng mặt bàn bằng cách ghép thêm (vào giữa) một mặt hình chữ nhật có một kích thước là 1,2 m (hình dưới)
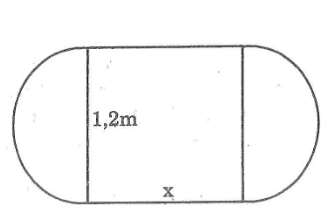
a. Kích thước kia của hình chữ nhật phải là bao nhiêu nếu diện tích mặt bàn tăng gấp đôi sau khi nới?
b. Kích thước kia của hình chữ nhật phải là bao nhiêu nếu chu vi mặt bàn tăng gấp đôi sau khi nới?
Lời giải:
a. Gọi x (m) là kích thước còn lại của hình chữ nhật
Điều kiện : x > 0
Ta có: 1,2x + π(0,6)2 = 2π(0,6)2
⇔ 1,2x = 2π(0,6)2 - π(0,6)2 =π0,36
⇔
Vậy kích thước còn lại của hình chữ nhật phải là 0,942m
b. Chu vi mặt bàn sau khi nới rộng là : π.1,2 + 2x (m)
Theo đề bài,chu vi của bàn tăng gấp đôi sau khi nới rộng. Ta có:
1,2π + 2.x = 2.1,2π
⇔ 2x =2,4π -1,2π = 1,2π
⇔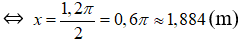
Vậy kích thước còn lại của hình chữ nhật phải là 1,884m
Bài 69 trang 112 Sách bài tập Toán 9 Tập 2: Cho đường tròn (O;R) chia đường tròn này thành ba cung có số đo tỉ lệ với 3,4,5.Tính diện tích các hình quạt tròn được tạo thành
Lời giải:
Gọi x,y,z lần lượt là số đo độ của ba cung
ta có: x + y + z = 360°
Theo đề bài ta có:
suy ra: x = 3.30° = 90° ; y = 4. 30° = 120°;z = 5. 30° = 150°
Diện tích hình quạt tương ứng với các cung 90°,120°,150° là :
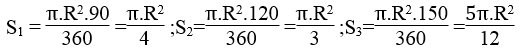
Bài 70 trang 112 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC nội tiếp trong đường tròn (O;R) có góc C =45°
a. Tính diện tích hình quạt tròn AOB(ứng với cung nhỏ AB)
b. Tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)
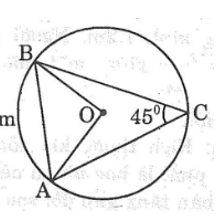
Lời giải:

Bài 71 trang 113 Sách bài tập Toán 9 Tập 2: Trong tam giác đều ABC ,vẽ những cung tròn đi qua tâm của tam giác và từng cặp đỉnh của nó. Cho biết cạnh tam giác bằng a,tính diện tích hình hoa thị gạch sọc
Lời giải:
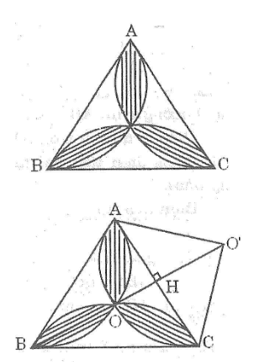
Gọi O là tâm của tam giác đều ABC
Ta có: OA =OB=OC
Vì ABC là tam giác đều nên AO,BO , CO là tia phân giác của góc A , góc B ,góc C trong ΔOAC ta có:

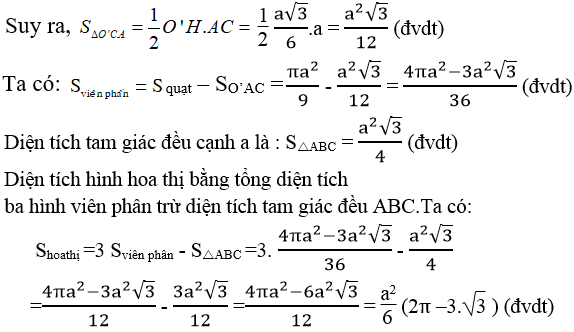
Bài 72 trang 113 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông ở A và đường cao AH.Vẽ đường tròn tam O đường kính AB.Biết BH = 2cm và HC = 6cm.Tính:
a.Diện tích hình tròn (O)
b.Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ)
c.diện tích hình quạt tròn AOH (ứng với các cung nhỏ AH)
Lời giải:
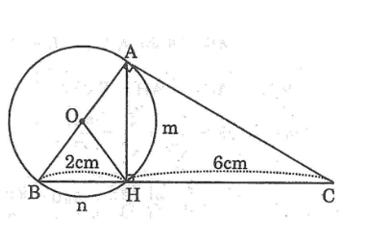
a) Trong tam giác ABC vuông tại A nên ta có:
AB2 = BH.BC =2.(2+6)=2.8=16
suy ra AB = 4cm
Diện tích hình tròn tâm (O) là :
S=π.(AB/2 )2= π.(4/2 )2 = 4π (cm2)
b) Trong tam giác vuông ABC có:
AH2 = HB.HC =2.6=12
Suy ra: AH =2.√3 cm
Diện tích tam giác AHB:
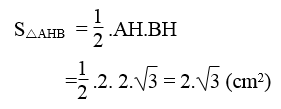
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O đường kính AB trừ diện tích tam giác AHB có:
c) Ta có AB=4cm ⇒ OB =2cm
Tam giác OBH có OB = OH =HB = 2cm nên tam giác OBH đều
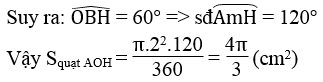
Bài 1 trang 113 Sách bài tập Toán 9 Tập 2: Tính diện tích của hình được giới hạn bởi các đường cong, biết OA = OB = R > 0 (h.bs.7).
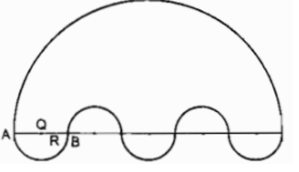
Lời giải:
Hình đó gồm nửa hình tròn bán kính 5R, 3 nửa hình tròn bán kính R và bớt đi 2 nửa hình tròn bán kính R.
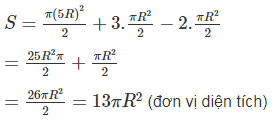
Bài 2 trang 113 Sách bài tập Toán 9 Tập 2: Tính diện tích của hình cánh hoa, biết OA = R (h.bs.8).
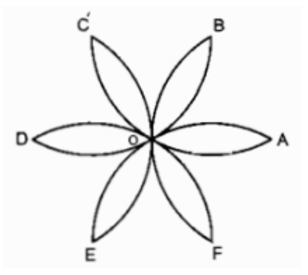
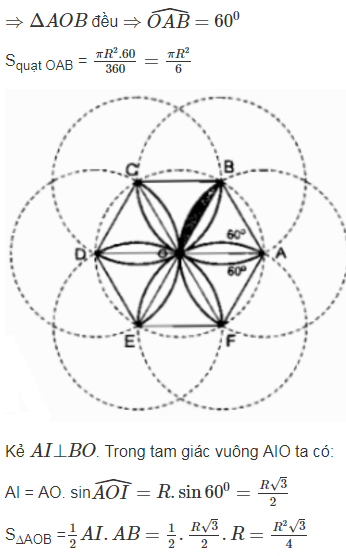
Lời giải:
Ta có 12 hình viên phân có diện tích bằng nhau tạo nên cánh hoa đó.
Xét hình viên phân giới hạn bởi cung BO và dây căng cung đó thì cung BO là cung của đường tròn tâm A bán kính R.
OA = AB = OB = R

Xem thêm Video Giải sách bài tập Toán lớp 9 (SBT Toán 9) hay và chi tiết khác:
- Ôn tập chương 3
- Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ
- Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
- Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu
Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:
- Giải bài tập Toán 9
- Chuyên đề Toán 9 (có đáp án - cực hay)
- Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
- Các dạng bài tập Toán 9 cực hay
- Đề thi Toán 9
- Đề thi vào 10 môn Toán
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Giải sách bài tập Toán 9 hay, chi tiết của chúng tôi được biên soạn bám sát nội dung Sách bài tập Toán 9 Tập 1 & Tập 2.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 9 Global Success
- Giải sgk Tiếng Anh 9 Smart World
- Giải sgk Tiếng Anh 9 Friends plus
- Lớp 9 Kết nối tri thức
- Soạn văn 9 (hay nhất) - KNTT
- Soạn văn 9 (ngắn nhất) - KNTT
- Giải sgk Toán 9 - KNTT
- Giải sgk Khoa học tự nhiên 9 - KNTT
- Giải sgk Lịch Sử 9 - KNTT
- Giải sgk Địa Lí 9 - KNTT
- Giải sgk Giáo dục công dân 9 - KNTT
- Giải sgk Tin học 9 - KNTT
- Giải sgk Công nghệ 9 - KNTT
- Giải sgk Hoạt động trải nghiệm 9 - KNTT
- Giải sgk Âm nhạc 9 - KNTT
- Giải sgk Mĩ thuật 9 - KNTT
- Lớp 9 Chân trời sáng tạo
- Soạn văn 9 (hay nhất) - CTST
- Soạn văn 9 (ngắn nhất) - CTST
- Giải sgk Toán 9 - CTST
- Giải sgk Khoa học tự nhiên 9 - CTST
- Giải sgk Lịch Sử 9 - CTST
- Giải sgk Địa Lí 9 - CTST
- Giải sgk Giáo dục công dân 9 - CTST
- Giải sgk Tin học 9 - CTST
- Giải sgk Công nghệ 9 - CTST
- Giải sgk Hoạt động trải nghiệm 9 - CTST
- Giải sgk Âm nhạc 9 - CTST
- Giải sgk Mĩ thuật 9 - CTST
- Lớp 9 Cánh diều
- Soạn văn 9 Cánh diều (hay nhất)
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Toán 9 - Cánh diều
- Giải sgk Khoa học tự nhiên 9 - Cánh diều
- Giải sgk Lịch Sử 9 - Cánh diều
- Giải sgk Địa Lí 9 - Cánh diều
- Giải sgk Giáo dục công dân 9 - Cánh diều
- Giải sgk Tin học 9 - Cánh diều
- Giải sgk Công nghệ 9 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 9 - Cánh diều
- Giải sgk Âm nhạc 9 - Cánh diều
- Giải sgk Mĩ thuật 9 - Cánh diều

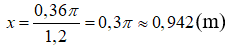
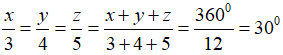
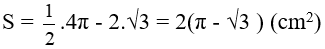



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

