Sách bài tập Toán 9 Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)

Sách bài tập Toán 9 Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)

Bài 71 trang 168 Sách bài tập Toán 9 Tập 1: Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I; IA) và (B; BA).

a. Hai đường tròn (I) và (B) nói trên có vị trí tương đối như thế nào với nhau? Vì sao?

b. Kẻ một đường thẳng đi qua A, cắt các đường tròn (I) và (B) theo thứ tự tại M và N. So sánh các độ dài AM và MN.

Lời giải:

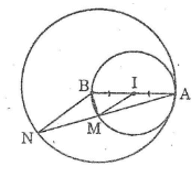
a. Vì A, I, B thẳng hàng nên:

BI = AB – AI

Vậy đường tròn (I; IA) tiếp xúc với đường tròn (B; BA) tại A.

b. Tam giác AMB nội tiếp trong đường tròn (I) có AB là đường kính nên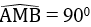

Suy ra: AM ⊥ BM hay BM ⊥ AN

Suy ra: AM = MN (đường kính vuông góc dây cung).

Bài 72 trang 169 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C). So sánh các độ dài AC và BD.

Lời giải:

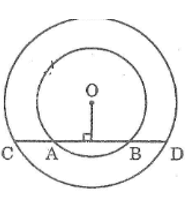
Kẻ OI ⊥ AB. Ta có: OI ⊥ CD

Trong đường tròn (O) (nhỏ) ta có : OI ⊥ AB

Suy ra :

IA = IB (đường kính vuông góc dây cung)    (1)

Trong đường tròn (O) (lớn) ta có : OI ⊥ CD

Suy ra :

IC = ID (đường kính vuông góc dây cung)

Hay IA + AC = IB + BD     (2)

Từ (1) và (2) suy ra: AC = BD.

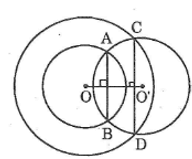
Bài 73 trang 169 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn (C ∈ (O), D ∈ (O’))

a. Tính số đo góc CAD

b. Tính độ dài CD biết OA = 4,5cm, O’A = 2cm

Lời giải:

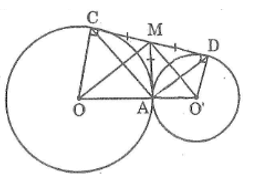
a. Kẻ tiếp tuyến chung tạ IA cắt CD tại M

Trong đường tròn (O) ta có:

MA = MC (tính chất hai tiếp tuyến cắt nhau)

Trong đường tròn (O’) ta có :

MA = MD (tính chất hai tiếp tuyến cắt nhau)

Suy ra : MA = MC = MD = 12 CD

Tam giác ACD có đường trung tuyến AM ứng với cạnh CD bằng nửa cạnh CD nên tam giác ACD vuông tại A

Suy ra :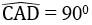

b. Ta có :

MO là tia phân giác của góc (CMA) (tính chất hai tiếp tuyến cắt nhau)

MO’ là tia phân giác của góc (DMA) (tính chất hai tiếp tuyến cắt nhau)

Suy ra : MO ⊥ MO’ (tính chất hai góc kề bù)

Tam giác MOO’ vuông tại M có MA ⊥ OO’ (tính chất tiếp tuyến)

Theo hệ thức lượng trong tam giác vuông, ta có :

MA² = OA.O’A = 4,5.2 = 9 ⇒ MA = 3 (cm)

Mà MA = 12 CD ⇒ CD = 2.MA = 2.3 = 6 (cm)

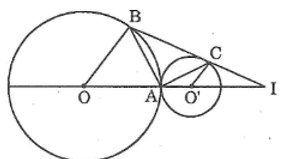
Bài 74 trang 169 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.

Lời giải:

Vì đường tròn (O’) cắt đường tròn (O ; OA) tại A và B nên OO’ là trung trực của AB

Suy ra : OO’ ⊥ AB     (1)

Vì đường tròn (O’) cắt đường tròn (O ; OC) tại C và D nên OO’ là trung trực của CD

Suy ra : OO’ ⊥ CD     (2)

Từ (1) và (2) suy ra : AB // CD.

Bài 75 trang 169 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O ; 3cm) và đường tròn (O’; 1cm) tiếp xúc ngoài tại A. Vẽ hai bán kính OB và O’C song song với nhau thuộc cùng nửa mặt phẳng có bờ OO’.

a. Tính số đo góc BAC.

b. Gọi I là giao điểm của BC và OO’. Tính độ dài OI.

Lời giải:

a. Ta có : OB // O’C (gt)

Suy ra : (hai góc trong cùng phía)

OA = OB (=R)

⇒ Tam giác AOB cân tại O

Bài 76 trang 169 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn (D ∈ (O), E ∈ (O’)). Gọi M là giao điểm của BD và CE.

a. Tính số đo góc DAE.

b. Tứ giác ADME là hình gì? Vì sao ?

c. Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn.

Lời giải:

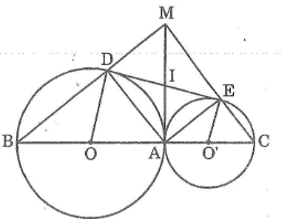
a. Kẻ tiếp tuyến chung tại A cắt DE tại I

Trong đường tròn (O) ta có:

IA = ID (tính chất hai tiếp tuyến cắt nhau)

Trong đường tròn (O’) ta có :

IA = IE (tính chất hai tiếp tuyến cắt nhau)

Suy ra : IA = ID = IE = (1/2).DE

Tam giác ADE có đường trung tuyến AI ứng với cạnh DE và bằng nửa cạnh DE nên tam giác ADE vuông tại A

Suy ra: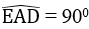

b. Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên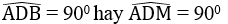

Tam giác AEC nội tiếp trong đường tròn (O’) có AC là đường kính nên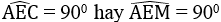

Mặt khác: 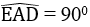(chứng minh trên)

Tứ giác ADME có ba góc vuông nên nó là hình chữ nhật.

c. Tứ giác ADME là hình chữ nhật và ID = IE (chứng minh trên) nên đường chéo AM của hình chữ nhật phải đi qua trung điểm I của DE. Suy ra: A, I, M thẳng hàng.

Ta có: IA ⊥ OO’ (vì IA là tiếp tuyến của (O))

Suy ra: AM ⊥ OO’

Vậy MA là tiếp tuyến chung của đường tròn (O) và (O’)

Bài 77 trang 169 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng:

a. MNQP là hình thang cân.

b. PQ là tiếp tuyến chung của hai đường tròn (O) và (O’).

c. MN + PQ = MP + NQ.

Lời giải:

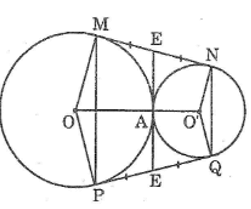
a. Vì M và P đối xứng qua trục OO’ nên OO’ là đường trung trực của MP

Suy ra: OP = OM

Khi đó P thuộc (O) và MP ⊥ OO’    (1)

Vì N và Q đối xứng qua trục OO’ nên OO’ là đường trung trực của NQ

Suy ra: O’N = O’Q

Khi đó Q thuộc (O’) và NQ ⊥ OO’    (2)

Từ (1) và (2) suy ra: MP // NQ

Tứ giác MNQP là hình thang

Vì OO’ là đường trung trực của MP và NQ nên OO’ đi qua trung điểm hai đáy hình thang MNQP, OO’ đồng thời cũng là trục đối xứng của hình thang MNQP nên MNQP là hình thang cân.

b. Ta có: MN ⊥ OM (tính chất tiếp tuyến)

Suy ra: QP ⊥ OP tại P

Vậy PQ là tiếp tuyến của đường tròn (O).

Ta có: MN ⊥ O’N (tính chất tiếp tuyến)

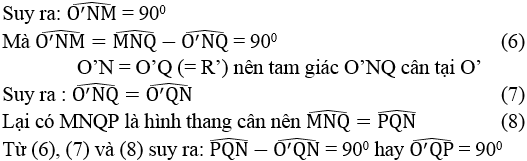
Suy ra: QP ⊥ O’Q tại Q

c. Kẻ tiếp tuyến chung tại A cắt MN tại E và PQ tại F

Trong đường tròn (O), theo tính chất hai tiếp tuyến cắt nhau, ta có:

EM = EA và FP = FA

Trong đường tròn (O’), theo tính chất hai tiếp tuyến cắt nhau, ta có:

EN = EA và FQ = FA

Suy ra: EM = EA = EN = (1/2).MN

FP = FA = FQ = (1/2).PQ

Suy ra : MN + PQ = 2EA + 2FA = 2(EA + FA) = 2EF    (9)

Vì EF là đường trung bình của hình thang MNQP nên :

EF = (MP + NQ)/2 hay MP + NQ = 2EF    (10)

Từ (9) và (10) suy ra: MN + PQ = MP + NQ

Bài 78 trang 170 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; 2cm), (O’; 3cm), OO’ = 6cm

a. Hai đường tròn (O) và (O’) có vị trí tương đối như thế nào với nhau?

b. Vẽ đường tròn (O’; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó (A là tiếp điểm). Tia O’A cắt đường tròn (O’; 3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O’B, B và C thuộc cùng một nửa mặt phẳng có bờ OO’. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O; 2cm), (O’; 3cm).

c. Tính độ dài BC

d. Gọi I là giao điểm của BC và OO’/ Tính độ dài IO

Lời giải:

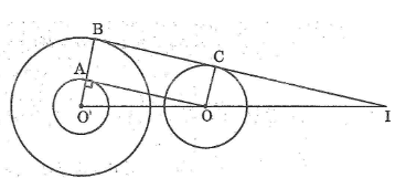
a. Vì OO’ = 6 > 2 + 3 hay OO’ > R + R’ nên hai đường tròn (O) và (O’) ở ngoài nhau.

b. Xét tứ giác ABCO ta có:

AB // CO (gt)    (1)

Mà : AB = O’B – O’A = 3 – 1 = 2    (cm)

Suy ra: AB = OC = 2 (cm) (2)

Từ (1) và (2) suy ra: ABCO là hình bình hành

Lại có: OA ⊥ O’A (tính chất tiếp tuyến)

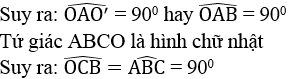
Suy ra: BC ⊥ OC và BC ⊥ O’B

Vậy BC là tiếp tuyến chung của hai đường tròn (O) và (O’)

c. Vì tứ giác ABCO là hình chữ nhật nên OA = BC

Áp dụng định lí Pitago vào tam giác vuông OAO’, ta có:

OO’² = OA² + O’A²

⇒ OA² = OO’² – O’A² = 6² – 1² = 35 ⇒ OA = √35 (cm)

Vậy BC = 35 (cm)

d. Trong tam giác O’BI có OC // O’B

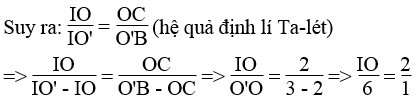
Vậy OI = (6.2)/1 = 12 (cm)

Bài 79 trang 170 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A; 2R)

a. Hai đường tròn (O) và (A) có vị trí tương đối như thế nào với nhau?

b. Gọi B là một giao điểm của hai đường tròn trên. Vẽ đường kính BOC của đường tròn (O). Gọi D là giao điểm (khác C) của AC và đường tròn (O). Chứng minh rằng AD = DC

Lời giải:

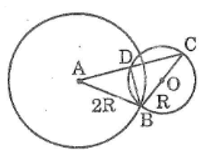
a. Ta có: R < OA < 3R ⇔ 2R – R < OA < 2R + R

Suy ra hai đường tròn (O ; R) và (A ; 2R) cắt nhau

b. Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên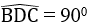

Suy ra : BD ⊥ AC     (1)

Ta có : AB = 2R và BC = 2OB = 2R

Suy ra tam giác ABC cân tại B    (2)

Từ (1) và (2) suy ra : AD = DC

Bài 80 trang 170 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O).

Lời giải:

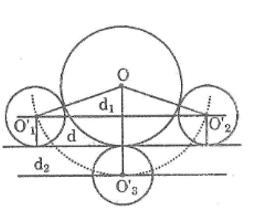
* Phân tích

- Giả sử dựng được đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O; 2cm).

- Đường tròn (O’; 1cm) tiếp xúc với d nên O’ cách d một khoảng bằng 1cm. Khi đó O’ nằm trên hai đường thẳng d₁, d₂ song song với d và cách d một khoảng bằng 1cm.

- Đường tròn (O’; 1cm) tiếp xúc với đường tròn (O; 2cm) nên suy ra OO’ = 3cm. Khi đó O’ là giao điểm của (O; 3cm) với d₁ và d₂

* Cách dựng

- Dựng hai đường thẳng d1 và d2 song song với d và cách d một khoảng bằng 1cm.

- Dựng đường tròn (O; 3cm) cắt d₁ tại O’₁. Vẽ (O’₁; 1cm) ta có đường tròn cần dựng

* Chứng minh

Theo cách dựng, O’₁ cách d một khoảng bằng 1cm nên (O’1; 1cm) tiếp xúc với d.

Vì OO’₁ = 3cm nên (O’₁; 1cm) tiếp xúc với (O; 2cm)

* Biện luận: O các d₁ một khoảng bằng 1cm nên (O; 3cm) cắt d1 tại hai điểm phân biệt.

Bài 1 trang 170 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O;R) và (O’;r). Điền vào chỗ trống của bảng sau:

R	r	OO’	Hệ thức giữa OO’, R, r	Vị trí tương đối của (O) và (O’)
3	1	.....	OO’ = R - r	.....
3	1	.....	.....	Tiếp xúc ngoài
3	1	3,5	.....	.....
3	1	5	.....	.....
3	1	1	.....	.....

Lời giải:

R	r	OO’	Hệ thức giữa OO’, R, r	Vị trí tương đối của (O) và (O’)
3	1	2	OO’ = R - r	Tiếp xúc trong
3	1	4	OO’ = R + r	Tiếp xúc ngoài
3	1	3,5	R – r < OO’ < R + r	Cắt nhau
3	1	5	OO’ > R + r	Ở ngoài nhau
3	1	1	OO’ < R - r	(O) đựng (O’)

Bài 2 trang 170 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O; 3cm) và (O’; 4cm) có OO’ = 5cm.

a) Hai đường tròn (O) và (O’) có vị trí tương đối nào?

b) Tính độ dài dây chung của hai đường tròn.

Lời giải:

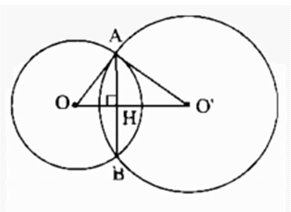
a) Gọi (O) và (O’) cắt nhau.

b) Gọi A và B là giao điểm của hai đường tròn (O) và (O’), H là giao điểm của AB và OO’.

Tam giác AOO’ vuông tại A, AH ⏊ OO’ và AB = 2AH.

Ta tính được AH = 2,4cm nên AB = 4,8cm.

Bài 3 trang 171 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn.

a) Chứng minh rằng trung điểm M của AB chuyển động trên một đường tròn (O’).

b) Đường tròn (O’) có vị trí tương đối nào với đường tròn (O) ?

Lời giải:

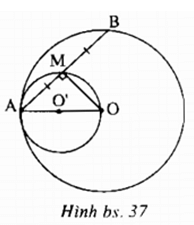
a) ∠(AMO) = 90^o. Điểm M chuyển động trên đường tròn (O’) đường kính AO.

b) Đường tròn (O’) tiếp xúc trong với đường tròn (O).

Xem thêm Video Giải sách bài tập Toán lớp 9 (SBT Toán 9) hay và chi tiết khác:

• Ôn tập chương 2
• Bài 1: Phương trình bậc nhất hai ẩn
• Bài 2: Hệ hai phương trình bậc nhất hai ẩn
• Bài 3: Giải hệ phương trình bằng phương pháp thế

Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:

• Giải bài tập Toán 9
• Chuyên đề Toán 9 (có đáp án - cực hay)
• Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
• Các dạng bài tập Toán 9 cực hay
• Đề thi Toán 9
• Đề thi vào 10 môn Toán

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---