Quy tắc đếm (Lý thuyết Toán lớp 10) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 10 Bài 23: Quy tắc đếm sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 10 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Quy tắc đếm (Lý thuyết Toán lớp 10) | Kết nối tri thức

Lý thuyết Quy tắc đếm

1. Quy tắc cộng và sơ đồ cây

Giả sử một công việc nào đó có thể thực hiện theo một trong hai phương án khác sau:

- Phương án một có n₁ cách thực hiện,

- Phương án hai có n₂ cách thực hiện (không trùng với bất kì cách thực hiện nào của phương án một).

Khi đó số cách thực hiện công việc sẽ là: n₁ + n₂ cách.

Chú ý:

- Sơ đồ minh hoạ cách phân chia trường hợp được gọi là sơ đồ hình cây.

- Trong bài toán đếm, người ta thường dùng sơ đồ hình cây để minh họa, giúp cho việc đếm thuận tiện và không bỏ sót trường hợp.

- Ta áp dụng quy tắc cộng cho một công việc có nhiều phương án khi các phương án đó phải rời nhau, không phụ thuộc vào nhau (độc lập với nhau).

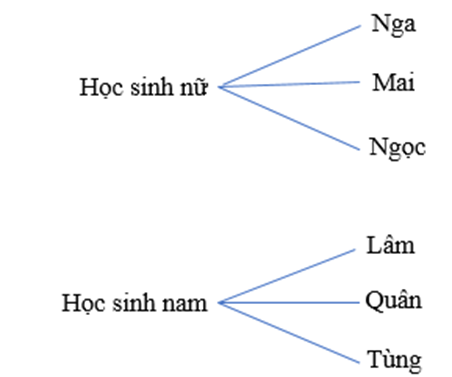
Ví dụ: Lớp 10A có 3 bạn nữ ưu tú là Nga, Mai, Ngọc và có 3 bạn nam ưu tú là Lâm, Quân, Tùng. Cô giáo muốn lấy ra một trong các bạn đó làm lớp trưởng của lớp. Hỏi cô giáo có bao nhiêu cách để chọn?

Hướng dẫn giải

Ta có sơ đồ hình cây minh họa các cách lựa chọn như sau:

Để lựa chọn một học sinh làm lớp trưởng, cô giáo có hai phương án:

Phương án 1: Chọn một học sinh nữ làm lớp trưởng, khi đó có n₁ = 3 (cách).

Phương án 2: Chọn một học sinh nam làm lớp trưởng, khi đó n₂ = 3 (cách).

Theo quy tắc cộng, số cách lựa chọn một học sinh làm lớp trưởng là:

n₁ + n₂ = 3 + 3 = 6 (cách).

Vậy cô giáo có 6 cách để chọn một trong số các bạn đó làm lớp trưởng.

2. Quy tắc nhân

Giả sử một công việc phải hoàn thành qua hai công đoạn liên tiếp nhau:

- Công đoạn một có m₁ cách thực hiện,

- Với mỗi cách thực hiện công đoạn một, có m₂ cách thực hiện công đoạn hai.

Khi đó số cách thực hiện công việc là m₁ . m₂ cách.

Chú ý: Quy tắc nhân áp dụng để tính số cách thực hiện một công việc có nhiều công đoạn, các công đoạn nối tiếp nhau và những công đoạn này độc lập với nhau.

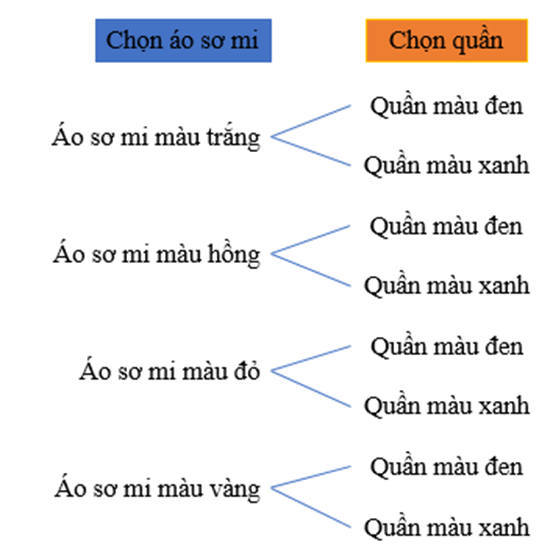
Ví dụ: Bạn Lan có có 4 chiếc áo sơ mi khác màu lần lượt là trắng, hồng, đỏ, vàng và 2 chiếc quần khác màu lần lượt là đen, xanh. Hãy cho biết bạn Lan có bao nhiêu cách để chọn một bộ gồm quần và áo.

Hướng dẫn giải

Để Lan chọn được một bộ quần áo phải qua hai công đoạn:

Chọn áo sơ mi → Chọn quần.

Ta có sơ đồ hình cây minh họa các cách lựa chọn như sau:

- Công đoạn 1: Chọn áo sơ mi có 4 cách chọn.

- Công đoạn 2: Ứng với mỗi cách chọn áo sơ mi có 2 cách chọn quần.

Áp dụng quy tắc nhân ta có 4.2 = 8 (cách) chọn một bộ gồm áo và quần.

Vậy bạn Lan có 8 cách để lựa chọn một bộ quần áo.

3. Kết hợp quy tắc cộng và quy tắc nhân

- Hầu hết các bài toán đếm trong thực tế sẽ phức tạp và thường phải áp dụng cả hai quy tắc cộng và nhân.

- Quy tắc cộng được áp dụng khi công việc được chia thành các phương án phân biệt (thực hiện một trong các phương án để hoàn thành công việc).

- Quy tắc nhân được áp dụng khi công việc có nhiều công đoạn nối tiếp nhau (phải thực hiện tất cả các công đoạn để hoàn thành công việc).

Ví dụ: Một nhà hàng chuẩn bị bữa sáng gồm hai loại đồ uống là nước ép hoa quả và trà. Nước ép hoa quả gồm có nước cam ép, nước ép dứa, nước ép dưa leo ; trà có hai loại là : trà xanh, trà nhài. Có 4 món ăn là cháo, bún, phở và cơm rang; 2 món tráng miệng là kem và sữa chua. Tính số cách để khách hàng chọn một khẩu phần ăn gồm đủ ba loại : 1 đồ uống, 1 món ăn và 1 món tráng miệng.

Hướng dẫn giải

Để khách hàng chọn một khẩu phần ăn gồm đủ ba loại : đồ uống, món ăn và món tráng miệng thì gồm có 3 công đoạn chọn:

Công đoạn 1: Lựa chọn đồ uống:

- Phương án 1: Chọn nước ép hoa quả có 3 (cách)

- Phương án 2: Chọn trà có 2 (cách)

Áp dụng quy tắc cộng ta có số cách chọn đồ uống là 3 + 2 = 5 (cách).

Công đoạn 2: Ứng với mỗi cách lựa chọn đồ uống thì có 4 cách để lựa chọn món ăn.

Công đoạn 3: Ứng với mỗi cách lựa chọn đồ uống và món ăn ở trên thì có 2 cách lựa chọn món tráng miệng.

Áp dụng quy tắc nhân ta có số cách chọn một khẩu phần ăn gồm đủ ba loại : 1 đồ uống, 1 món ăn và 1 món tráng miệng là : 5.4.2 = 40 (cách).

Vậy khách hàng có 40 cách chọn một khẩu phần ăn gồm đủ ba loại : 1 đồ uống, 1 món ăn và 1 món tráng miệng.

Bài tập Quy tắc đếm

Bài 1: Một cửa hàng có 4 loại kem và 5 loại bánh. Hỏi có bao nhiêu cách chọn mua một loại kem hoặc một loại bánh ở cửa hàng này?

Hướng dẫn giải

Để lựa chọn mua một loại kem hoặc một loại bánh ở cửa hàng này có hai phương án để lựa chọn:

- Phương án 1: Chọn kem có 4 (cách).

- Phương án 2: Chọn bánh có 5 (cách).

Áp dụng quy tắc cộng: số cách để chọn mua một loại kem hoặc một loại bánh là 4 + 5 = 9 (cách).

Vậy có 9 cách để chọn mua một loại kem hoặc một loại bánh từ cửa hàng đó.

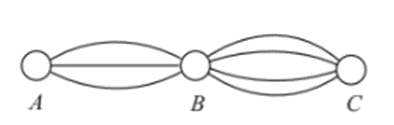
Bài 2: Từ vị trí A đến vị trí B có ba con đường, từ B đến C có bốn con đường. Hỏi có bao nhiêu cách để đi từ A đến C qua B.

Hướng dẫn giải

Để đi từ vị trí A đến vị trí C qua B, ta thực hiện hai công đoạn:

Công đoạn 1: Đi từ A đến B có 3 (cách).

Công đoạn 2: Ứng với mỗi cách đi từ A đến B, đi từ B đến C có 4 (cách).

Áp dụng quy tắc nhân ta có: Số cách đi từ A đến C là: 3.4 = 12 (cách).

Vậy có 12 cách đi từ A đến C.

Bài 3: Bạn Hoa dự định đi vào một cửa hàng để mua kem sau đó sẽ đi mua một cốc nước. Biết có hai loại kem để lựa chọn là kem que hoặc kem ốc quế. Kem que có 5 loại; kem ốc quế có 3 loại. Có ba loại nước là nước cam, nước dừa, nước mía. Hỏi có bao nhiêu cách để Hoa mua được một loại kem và một loại nước.

Hướng dẫn giải

Để Hoa mua được một loại kem và một loại nước, Hoa chia làm 2 công đoạn:

Công đoạn 1: Mua một loại kem :

Có 2 phương án để lựa chọn kem:

- Phương án 1: Lựa chọn kem que: có 5 (cách).

- Phương án 2: Lựa chọn kem ốc quế: có 3 (cách).

Áp dụng quy tắc cộng ta có: 5 + 3 = 8 (cách) lựa chọn kem.

Công đoạn 2: Ứng với một loại kem, mua một loại nước: có 3 (cách) lựa chọn.

Áp dụng quy tắc nhân ta có: Số cách lựa chọn một loại kem và một loại nước là 8.3 = 24 (cách).

Vậy có 24 cách để Hoa chọn một loại kem và một loại nước.

Học tốt Quy tắc đếm

Các bài học để học tốt Quy tắc đếm Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài 23: Quy tắc đếm

Xem thêm tóm tắt lý thuyết Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

• Lý thuyết Toán 10 Bài 24: Hoán vị, chỉnh hợp và tổ hợp

• Lý thuyết Toán 10 Bài 25: Nhị thức Newton

• Tổng hợp lý thuyết Toán 10 Chương 8

• Lý thuyết Toán 10 Bài 26: Biến cố và định nghĩa cổ điển của xác suất

• Lý thuyết Toán 10 Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

Xem thêm các tài liệu học tốt lớp 10 hay khác:

• Giải sgk Toán 10 Kết nối tri thức
• Giải Chuyên đề học tập Toán 10 Kết nối tri thức
• Giải SBT Toán 10 Kết nối tri thức
• Giải lớp 10 Kết nối tri thức (các môn học)
• Giải lớp 10 Chân trời sáng tạo (các môn học)
• Giải lớp 10 Cánh diều (các môn học)

---